隔爆型接线盖加强筋的优化设计及实验研究*
2021-09-15禹建勇武文俊
张 瑞,禹建勇,王 成,武文俊
(1.南京科远智慧科技集团股份有限公司,江苏 南京 211102; 2.江苏省热工过程智能控制重点实验室,江苏 南京 211102)
0 引 言
隔爆型执行机构广泛用于火电、石化、冶金等工业领域,常处于易燃易爆气体环境。接线盖安装于隔爆型执行机构接线腔的端部,保护接线腔内接线端子等一系列零部件,接线盖必须承受爆炸性气体混合物通过接线盖的隔爆结合面进入执行机构内部后爆炸但不损坏,同时不会因内部爆炸而引爆外部爆炸性气体[1],从而确保隔爆型执行机构的安全性能。接线盖的隔爆设计对隔爆型执行机构的隔爆性能具有重要意义。
目前多采用静压实验来验证接线盖是否满足隔爆标准,水压变化曲线为0~5 s,压力由0增加至2 MPa,保持10 s,最后5 s内压力逐渐完全释放[2]。在承受水压时,接线盖隔爆结合面与箱体隔爆结合面的配合间隙须满足隔爆标准规定的隔爆通道直径要求[1]。因此,隔爆型执行机构接线盖设计的关键点在于接线盖的隔爆结合面变形是否满足隔爆标准要求。但目前大多数隔爆型执行机构产品的接线盖并未进行专业的隔爆设计,大多依赖设计人员的工程经验,通过壁厚加厚,或盲目设置加强筋的方法增强接线盖刚度,缺乏系统的理论指导。
随着拓扑优化理论的不断发展与完善,拓扑优化技术被广泛应用到工程中[3-6]。拓扑优化技术中应用最为广泛的是变密度法,以变量的密度函数形式,显式地表达单元相对密度(在0~1之间连续变化)与材料弹性模量之间的关系,在给定的载荷及边界条件下,寻求结构最佳的传力路线,寻找设计区域内的材料分布的最优形式[7-10]。蔡安江等[7]采用拓扑优化方法对平模台振的振动台面加强筋布局进行优化,提高其振动效果。Dugré等[8]利用该技术研究矩形板的加强筋布局,并阐述了拓扑优化概念指导加强筋布局设计的思路。Jin等[9]采用拓扑优化方法得到重型立式车床工作台的初始加强筋结构,为加强筋结构的设计提供布局参考。宁晓斌等[10]采用拓扑优化方法,对液压挖掘机斗杆结构进行拓扑优化仿真,在保证强度的前提下降低了斗杆的质量。
拓扑优化的目的是在给定的设计域内寻找最优的材料分布[6-7],使结构获得优异的性能,在寻找最优加强筋布局方面有着巨大的潜力。但拓扑优化方法也存在一定的局限性,即优化结果存在大量的灰度单元,无法获得清晰的加强筋布局等,而这些缺陷,可通过擅长参数、尺寸优化方面的尺寸优化来弥补。
尺寸优化技术已大量应用于工程领域。禹建勇等[11]采用尺寸优化方法进行了自然对流散热器的结构设计。王静等[12]结合框架的应力情况,设定合理的优化目标,完成集成框架的尺寸优化。朱卓等[13]以横梁的几何参数为输入变量,重要力学参数为输出变量,得到筋板最优尺寸参数。高云凯等[14]采用尺寸优化和拓扑优化结合的方法,对白车身质量块安装点的动刚度进行优化,提高了安装点的动刚度。
基于此,为控制接线盖隔爆结合面的变形,使其满足隔爆标准要求,文中拟系统地开展隔爆执行机构接线盖的加强筋设计。主要步骤如下:①首先对隔爆接线盖进行结构拓扑优化分析,根据拓扑优化结果对接线盖进行加强筋的布局设计,确定基本筋型;②采用尺寸优化方法,对基本筋型加强筋的多个关键几何参数进行优化,确定最优筋型的详细尺寸;③综合考虑铸造工艺等因素确定最优加强筋模型;④最后进行产品打样,对样件接线盖进行静压实验,并与仿真结果及原接线盖实验结果对比,得到接线盖加强筋的最优筋型。
1 接线盖最优筋型优化设计
1.1 接线盖拓扑优化分析
现有接线盖三维模型如图1所示,在隔爆结合面内部的四根竖直筋即为原有的加强筋,但并未达到理想效果,只能通过加厚壁厚或盲目加筋来减小变形,但无疑会增加经济成本,且易引起铸造缺陷。

图1 现有接线盖三维模型 图2 拓扑优化设计模型
建立拓扑优化设计模型如图2所示。
分为设计区域及非设计区域,设计区域为需要进行筋型布局的区域,非设计区域为外观造型、螺钉孔等区域,已将原有竖直筋去除,且壁厚适当减薄,以达到轻量化设计目的。非设计区域结构特征保持不变,仅对设计区域进行拓扑优化分析。
拓扑优化设计需要设计变量,目标函数和约束条件三个要素,设计变量是允许发生改变的结构关键参数;目标函数是设计变量的函数;约束条件是对结构响应的限制条件。其数学模型可表述为:
目标函数Ft(x)=f(x1,x2,…,xi,xm)
t=1,…,k
约束条件Gj(x)≤0j=1,…,n
xiL≤xi≤xiUi=1,…,m
(1)
式中:x1,x2,…,xi,xm为设计变量,如关键尺寸,材料分布等;Ft(x)是目标函数,可为频率、质量、结构柔度等力学性能;Gj(x)是约束条件,如变形和应力等。在接线盖的拓扑优化仿真中,以接线盖结构柔度最小即刚度最大为优化目标,以单元相对密度作为设计变量,以体积分数为约束条件,进行拓扑优化仿真分析。
拓扑优化所需参数包括材料属性、载荷、边界条件以及材料去除体积比[6,15],主要分析流程为:定义材料属性,建立几何模型及划分网格,定义约束及载荷,设置拓扑优化参数,计算求解。常用接线盖的材料为高压铸造铝合金材料,其材料属性参数如表1所示。对接线盖的螺钉孔施加固定约束,对静压实验中高压水接触面施加保压阶段的压力2 MPa,即,只考虑保压阶段的载荷。对接线盖拓扑模型划分高精度网格单元数204 830,节点数352 979,网格质量较高,如图3所示。

表1 材料参数

图3 接线盖拓扑模型网格划分
经拓扑优化计算后,设计区域优化结果如图4(a)所示。可见,设计区域的材料去除部分主要集中在通过螺钉孔圆心的两条直径上,而保留了螺钉孔中间区域的材料。分析原因在于,接线盖通过螺钉孔安装固定,相当于增加了螺钉孔周围的结构刚度,相应的中间区域的刚度就相对较弱,成为止口变形的薄弱环节,约束的不均匀性,导致了变形的不均匀,此处加筋,使止口周向上刚度均一化。根据拓扑优化结果,进行接线盖加强筋的布局设计。综合考虑铸造工艺、模具设计、拔模角度、脱模工艺等因素,调整材料保留区域的筋型根数及布置角度,初步确定的筋型布局如图4(b)所示。在材料保留区域建立四组加强筋,每组有三根斜筋,沿周向成一定夹角分布,每组正中间一根斜筋连线为通过圆心的直径,且四组筋组成的两条直径相互垂直。
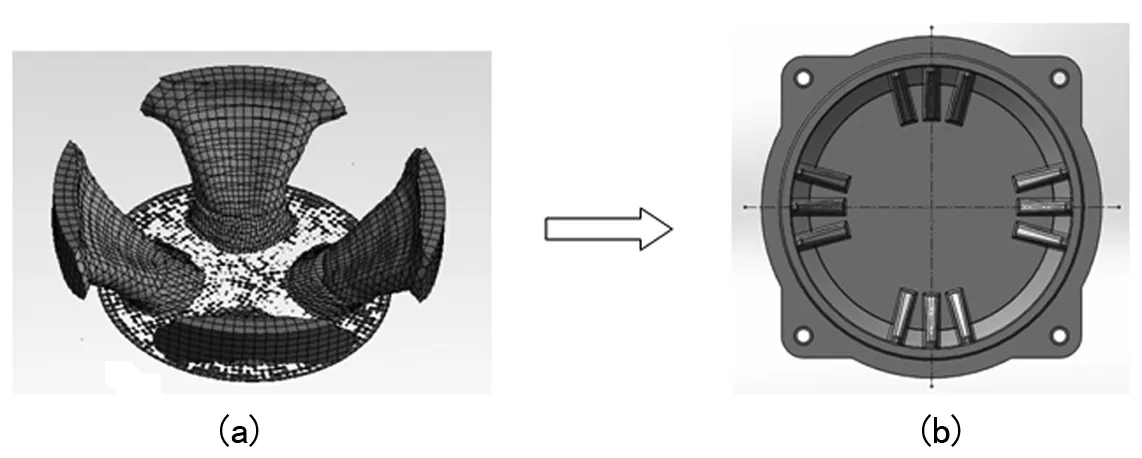
图4 接线盖拓扑优化后结果及筋型布局图
1.2 加强筋尺寸优化设计
虽然依据拓扑分析结果可以初步确定筋型布局,但不能确定加强筋的具体尺寸参数,主要包括加强筋与接线盖圆心的距离,加强筋的高度、相邻夹角等。因此,为更好的确定最优筋型,拟采用尺寸优化方法,探索加强筋的最优尺寸。尺寸优化方法是通过响应面来实现的,响应面是设计点的集合,设计点由Screening方法生成,Screening筛选优化方法基于采样和排序的简单方法,支持多种目标和约束以及所有类型的输入参数。
对接线盖加强筋进行参数化建模,文中拟优化的参数包括加强筋的根部与圆心的距离r,加强筋的高度h、加强筋相邻夹角θ,将其作为设计参数,限定三个参数的取值范围,如表2所列,上下限的取值依据接线盖装配空间及结构尺寸而定。需要指出的是,尺寸优化分析的约束与拓扑优化设计相同,而材料属性、载荷均有不同。其一,考虑到在约束位置,易产生应力集中,且YL113属于塑性材料,故对接线盖赋予塑性参数,允许进入弹塑性变形阶段[16];其二,实际静压实验中,测量隔爆结合面的直径变化量是在水压卸载之后测量,为与静压实验更好对应,尺寸优化仿真中施加与静压实验相同的压力载荷曲线,统计压力卸载后隔爆结合面的径向变形,即在局部圆柱坐标系中,结合面沿直径方向的变化量。接线盖加强筋尺寸优化设计的最终目标是在满足刚度和强度要求的前提下,接线盖的最大等效应力值小于许用应力值,即σmax≤[σ]=170 MPa,且隔爆结合面的径向最大变形量越小越好,从而最大程度减小隔爆结合面的变形,保证产品满足隔爆标准要求。
经过仿真计算,得出隔爆结合面变形量对各个参数的灵敏度柱状图,体现输入参数变化对输出量的影响以及对结构模型自身的影响,如图5可见,对接线盖隔爆面变形影响最大的为加强筋根部与圆心的距离,其次为加强筋夹角,加强筋高度影响最小。从输入参数组成的48组工况中,筛选出结合面变形最小时的最优尺寸组合,如表2所列,可见,加强筋根部与圆心的距离为52 mm,高度为26 mm,每组三根筋相互之间夹角15°时,接线盖隔爆结合面径向变形最小。

表2 尺寸优化参数选取范围及最优尺寸组合

图5 接线盖隔爆面变形对各参数的灵敏度柱状图
根据最优结果,综合考虑接线盖高压铸造工艺及修模经济成本,重建接线盖筋型模型。为保证接线盖内力传递的连续性更好,并进一步增强结构整体刚度,在接线盖加强筋根部建立圆形筋将四组加强筋连通,最终加强筋模型如图6所示。

图6 接线盖最终加强筋模型
将最新模型考虑塑性属性后重新仿真,该模型的变形及应力云图如图7~10所示。可见,接线盖的最大应力为186.2 MPa,整体最大变形为0.2 mm,隔爆结合面的最大应力为62.4 MPa,径向的最大变形,即影响隔爆间隙方向的最大变形为0.011 mm,满足隔爆标准要求[1]。

图7 接线盖最终加强筋模型应力云图 图8 接线盖最终加强筋模型位移云图

图9 接线盖最终加强筋模型隔爆面应力云图 图10 接线盖最终加强筋模型隔爆面径向位移云图
为进一步验证仿真结果,对接线盖加筋前后的模型进行简化,简化为内部受均布载荷的固支横跨梁,其简化示意图及剖面图如图11所示,固支位置为法兰面,内部水压为均布载荷。此处重点关注接线盖隔爆面端部的径向变形,近似于横跨梁的末端挠度,因此,由于固支位置接近梁末端,可近似为固支悬臂梁,故末端挠度公式为:
(2)
式中:E为弹性模量;I为截面轴惯性矩;q为均布载荷;l为梁的长度。可见,在载荷及材料相同的条件下,两种梁最主要差异在截面轴惯性矩参数I上,根据图11所示,推导出加筋前后两种梁的截面惯性矩可得:
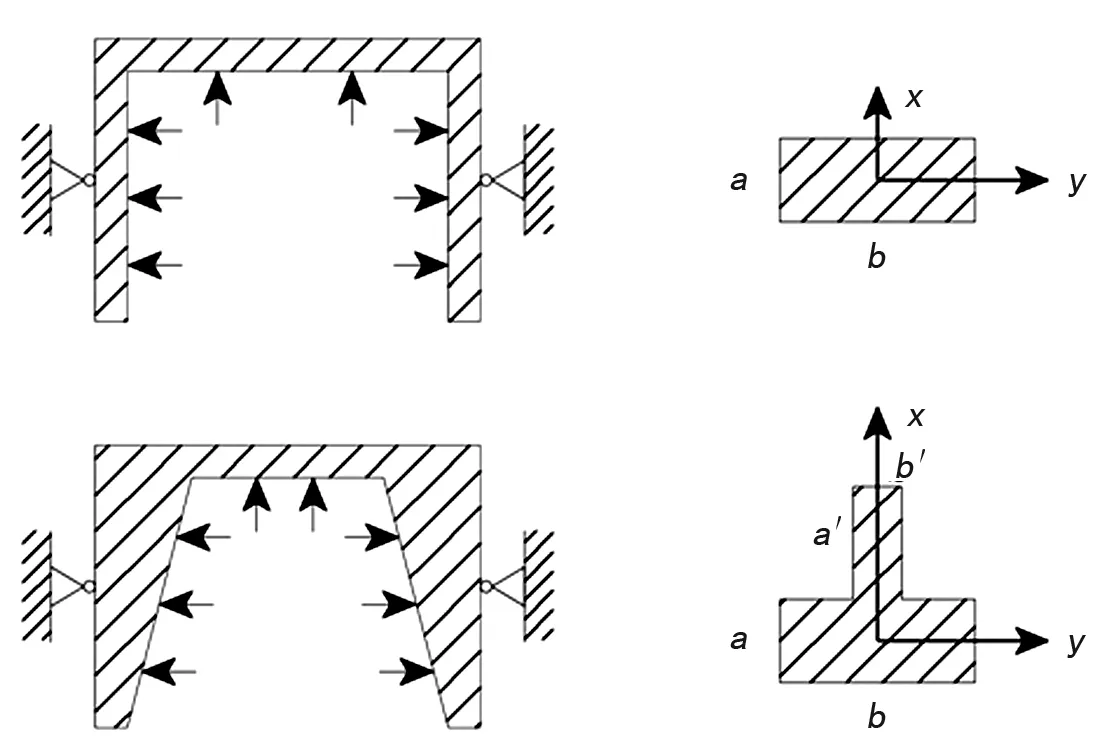
图11 接线盖加筋前后简化梁及剖面示意图
加筋前:
(3)
加筋后:
(4)
由公式(3)、(4)可见,加筋后,截面惯性矩I增大,而其余接线盖末端挠度成反比,故加筋后挠度减小,即接线盖隔爆结合面径向位移减小,与仿真结果一致。
1.3 静压实验测量
根据最优设计,进行优化后接线盖打样并进行静压实验验证,主要试验设备包括水压测试机、接线盖装配体、水压测试工装等。实验测试方法步骤及实验设备如参考文献[2]所示,水压测试机显示窗如图12所示。经过静压实验,接线盖表面无连续滴水,3次水压后接线盖表面无裂痕,隔爆结合面无损伤,5次水压后接线盖表面无明显裂纹产生,表明接线盖设计满足隔爆要求。进一步地,统计优化后接线盖隔爆结合面上端面直径变化,并与优化前对比,如表3所列。

图12 水压测试机显示窗 图13 接线盖静压实验测点位置示意图

表3 接线盖优化前后静压实验结果对比
表中直径ABCD位置如图13所示,且与优化前接线盖静压实验的测量点位置相同。从表中可见,优化前,接线盖测点直径变化量最大0.07 mm,圆度最大0.17 mm,优化后,各测点直径变化均在0.04 mm以内,且直径B、D基本不变形,优化后圆度小于等于0.05 mm,比优化前圆度减小约71%,达到了良好的优化效果。
2 结 语
针对目前隔爆执行机构接线盖加强筋设计缺乏理论依据的现状,开展接线盖的筋型优化仿真分析,采用拓扑优化技术与尺寸优化技术相结合的方法,用拓扑优化方法,确定大致筋型和布局,而后用尺寸优化方法,确定加强筋的详细尺寸,并结合力传递的连续性理论,最终确定最优筋型,最后,通过实验验证,优化后隔爆结合面圆度降低71%,达到了隔爆标准要求,证明该加强筋筋型优化效果明显。本文采用的系统的隔爆型加强筋的优化设计方法,不仅实现了接线盖的轻量化设计,降低了经济成本,而且提高了产品整体的隔爆性能,为隔爆型执行机构接线盖的加强筋设计提供理论依据。
