高超声速气动热/结构温度场一体化耦合分析

黄 杰，姚卫星,2，单先阳

(1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016) (2.南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏 南京 210016) (3.湖北航天技术研究院总体设计所，湖北 武汉 430040)

高超声速是未来军用飞行器发展的一个重要方向，近年来各国陆续开展了多个型号高超声速飞行器的研制，如美国的X-37B空天飞机和HTV-2助推/滑翔式弹道导弹等。高超声速飞行器区别于常规超声速飞行器的一个巨大特征是承受巨大的气动加热效应[1-3]，尤其是头锥和机翼前缘区域。在气动加热作用下飞行器机体结构温度将急剧升高。为了保证高温区域结构在材料允许的温度范围内，在设计时必须进行机体结构温度场的分析，这对高超声速飞行器的安全性至关重要。

早期的高超声速飞行器气动加热分析采用参考焓等工程方法[4]，其计算精度较低，已无法满足现代高超声速飞行器气动加热的高精度分析要求。现阶段主要采用计算流体动力学(computational fluid dynamics，CFD)数值方法进行飞行器气动加热的精确分析，其能获得满意的壁面热流分布[5-6]。在此基础上通过有限元等方法即可计算机体结构的温度场，评估结构的危险程度。目前广泛采用以上数值方法进行高超声速飞行器气动加热和结构温度场的分析，但其并未考虑结构温度升高对气动加热的影响[7-8]，在一定程度上会降低计算精度。

基于以上方法的不足，本文采用基于有限体积法的一体化耦合方法进行了高超声速钝头体的气动加热和结构温度场的耦合分析，充分考虑了壁面温度对壁面热流的影响，并研究了时间步长对收敛性的影响及壁面热流和壁面温度的时间历程。

1 基于有限体积法的一体化耦合分析方法

本文采用的一体化耦合分析方法如图1所示。其中流场计算是为了获得壁面热流分布，Δt为时间步长，且流场和结构温度场均采用有限体积法计算。在耦合分析开始前需要准备流场和结构传热分析的数值模型，定义结构的初始温度，并进行初始流场的计算，获得初始壁面热流分布。图中的步骤1将初始壁面热流分布传递给结构传热分析模型，并进行步骤2的结构温度场计算，获得Δt时刻的壁面温度分布。步骤3将Δt时刻的壁面温度分布传递给流场分析模型，并进行步骤4的流场计算，获得Δt时刻的壁面热流分布。此时Δt时刻的壁面热流和壁面温度分布都已计算得到，从步骤5开始进行2Δt时刻的结果分析。按照以上的方法进行时间推进即可获得各个时刻的壁面热流和壁面温度分布。

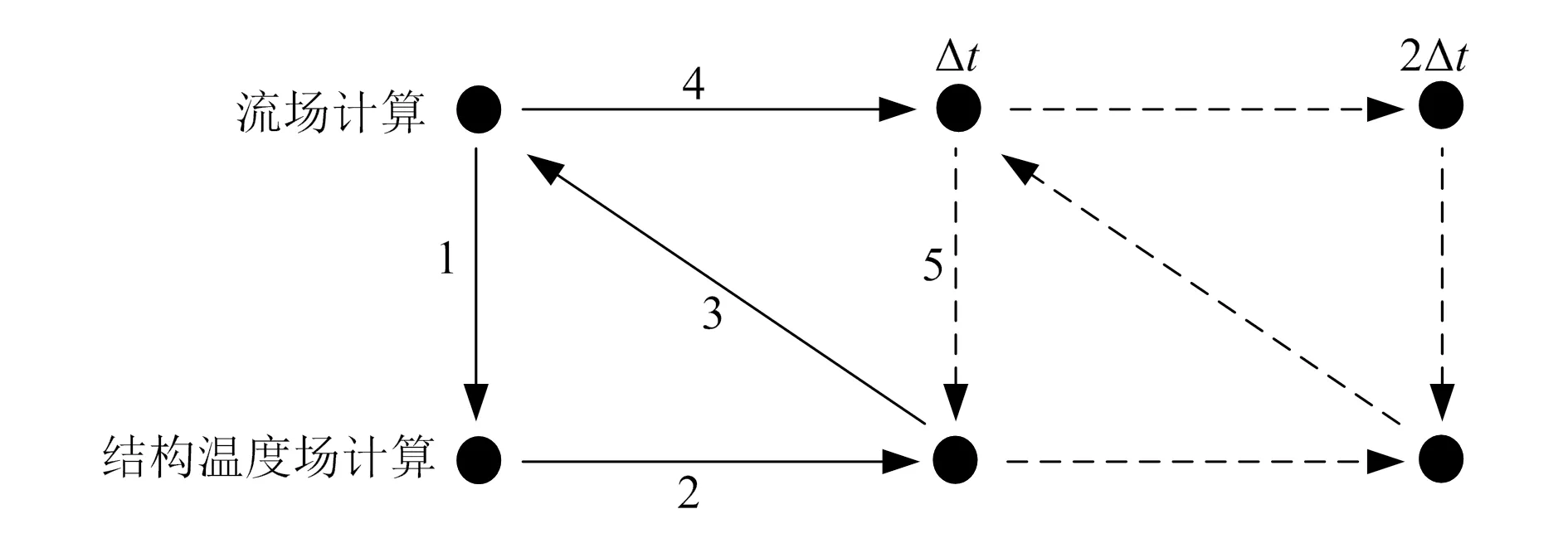
图1 一体化耦合分析方法

由于流场和结构温度场均采用有限体积法计算，因此可进行流场和结构计算网格的整体划分，这样流场和结构共用相同交界面和节点，方便壁面热流和壁面温度的数据传递。

2 高超声速钝头体气动热/结构温度场耦合分析

2.1 几何和数值模型

本文采用一体化耦合方法进行典型高超声速钝头体的分析。钝头体为一个半球体，如图2所示。球体的半径为30 mm，壁厚为8 mm，且其最左端恰好为钝头体的驻点。表1列出了自由来流的马赫数Ma∞、静压P∞、静温T∞及攻角α，其中马赫数已达到了7，是典型的高超声速流动。表2列出了钝头体材料的密度ρ、导热系数k及比热容c。

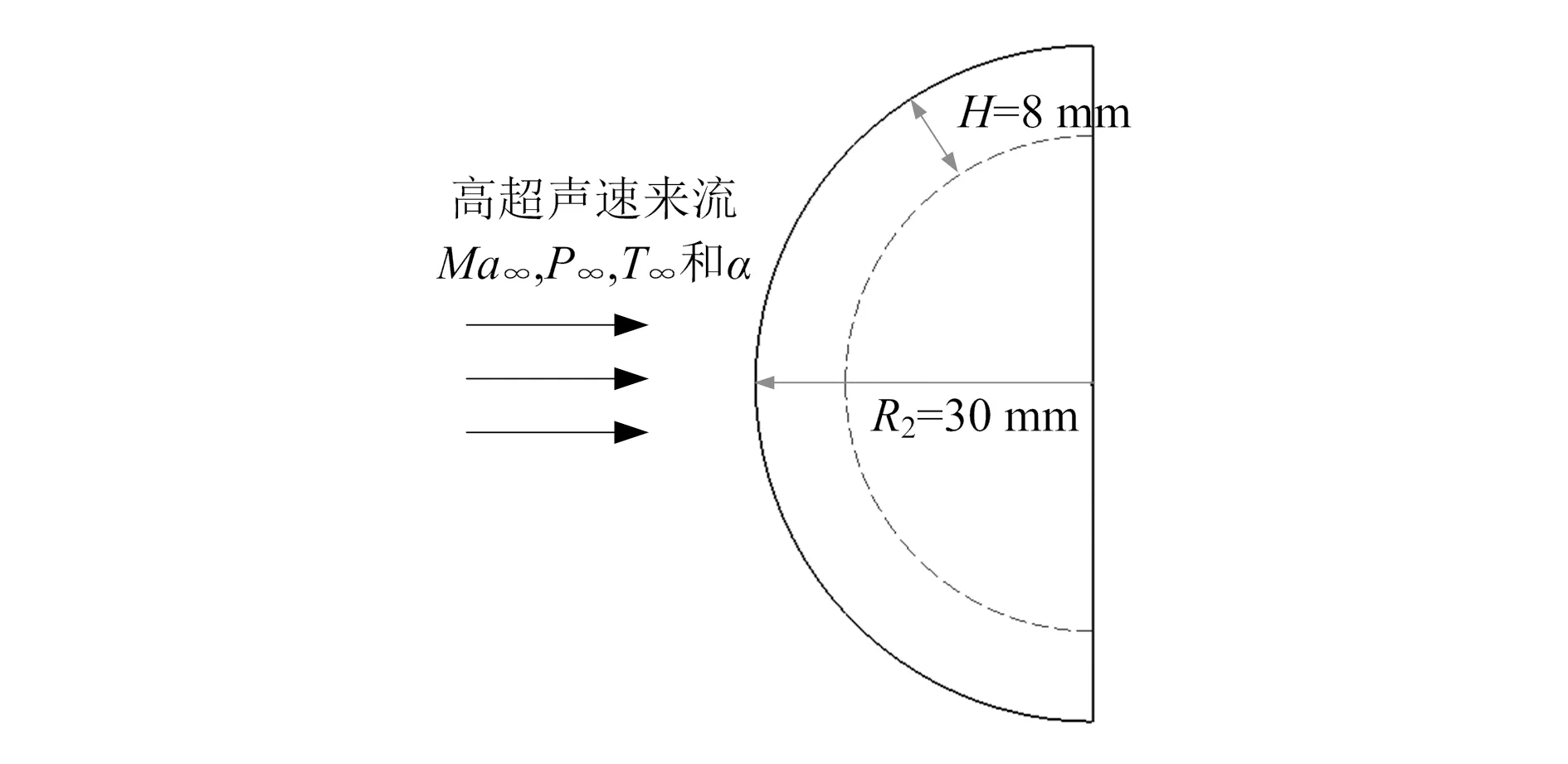
图2 钝头体几何模型

表1 自由来流参数

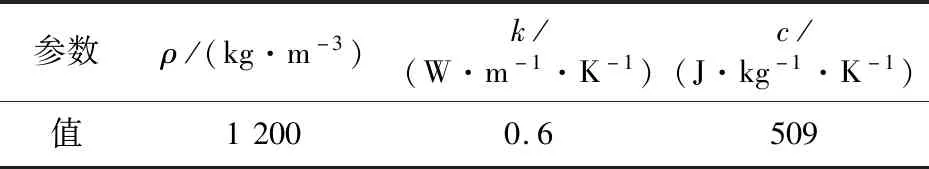
表2 结构材料参数

为了节约计算资源，本文建立了轴对称的计算模型，其计算网格及边界条件如图3所示。其中的流场区域在激波位置进行了局部网格加密。流场空间离散采用AUSM+格式[9]，湍流模型采用Menter's SSTk-ω两方程模型[10]，采用双时间步长法进行时间推进[11]。流场壁面第一层网格高度为0.001 mm，以满足Menter's SSTk-ω湍流模型的要求。流场分析模型的边界条件包括远场、超声速出口、对称轴及流/固交界面(耦合面)。结构区域的初始温度为300 K。结构传热分析模型的边界条件包括流/固交界面、对称轴、定温面(钝头体内壁面温度固定在300 K)及绝热面。此外为了研究时间步长对一体化耦合分析收敛性的影响，本文同时采用0.001 s和0.000 1 s两个时间步长进行分析。

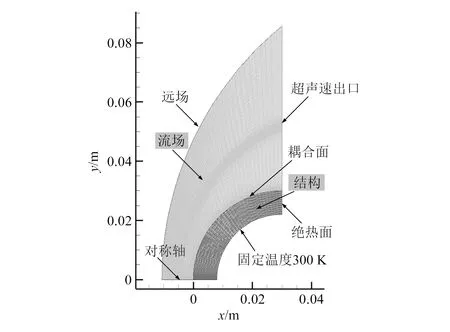
图3 计算网格及边界条件

2.2 初始流场

在进行一体化耦合分析前需要进行初始流场的计算，以便为后续的耦合分析提供初始壁面热流分布。图4给出了流场初始马赫云图和温度云图，结果表明高超声速来流受到钝头体的压缩在钝头体前方形成了一道离体激波。离体激波在驻点区域附近近似为正激波，波后马赫数小于1。沿钝头体往下游移动，离体激波强度逐渐降低并逐渐转换为斜激波，波后马赫数逐渐增大并最终大于1。此外驻点前方激波层内气体的最高温度达到了2 640 K，其与初始壁面温度300 K之间形成巨大的温度梯度，从而向钝头体传递大量的热量，造成气动加热效应，导致结构温度升高。

图4 流场初始马赫云图和温度云图

2.3 一体化耦合分析结果

计算获得初始壁面热流分布后即可按照图1中的一体化耦合分析方法进行本文钝头体的气动加热/结构温度场耦合计算，且耦合计算的总时间为12 s。图5给出了时间步长Δt为0.000 1 s时计算获得的钝头体壁面压力和壁面热流分布的时间历程。结果表明，耦合计算时间从0 s到12 s，钝头体壁面压力分布基本保持不变，这是由于壁面压力受边界层内气体热力学特性影响较小的原因。此外钝头体壁面热流分布随耦合计算时间的增加逐渐降低，且热流分布曲线之间的距离逐渐减小，表明钝头体壁面热流分布的变化率逐渐降低。此现象是由壁面温度升高导致边界层与壁面之间温度梯度减小造成的。

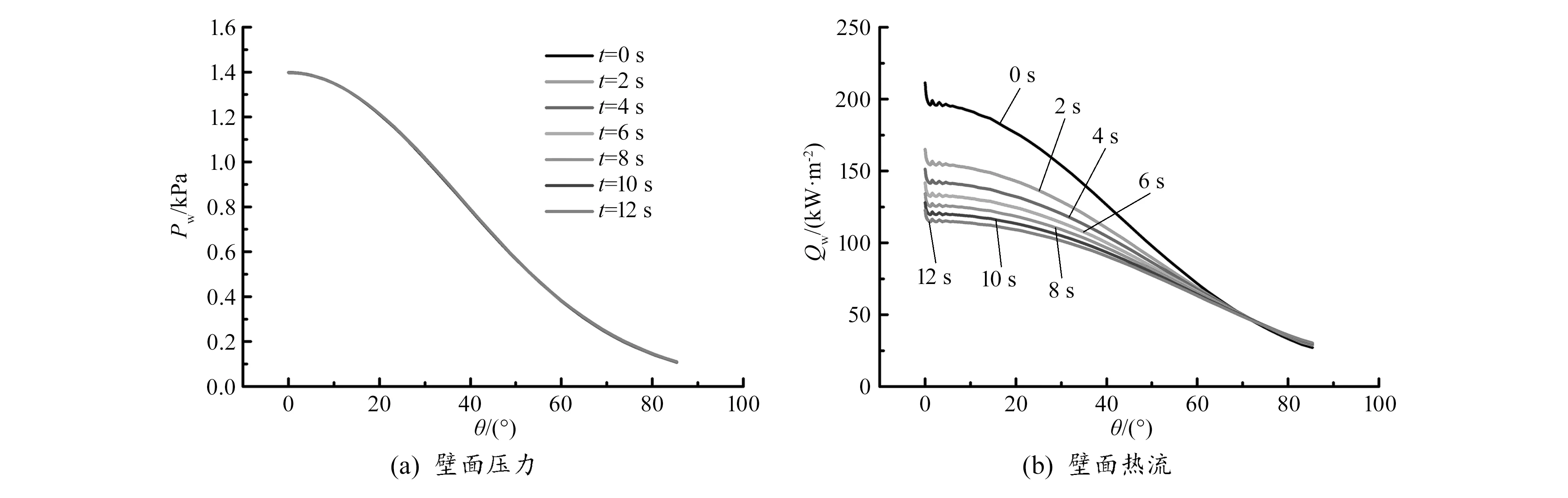
图5 壁面压力和壁面热流分布的时间历程(Δt=0.000 1 s)

图6(a)给出了时间步长Δt为0.001 s和0.000 1 s时计算得到的钝头体驻点温度的时间历程，结果表明在以上两个时间步长下计算获得的驻点温度时间历程一致。由图可知，本文的一体化耦合分析方法在时间步长为0.001 s时即可获得收敛的分析结果，该时间步长可作为其他高超声速飞行器气动加热/结构温度场一体化耦合分析的参考值。图6(b)给出了时间步长Δt为0.000 1 s时计算获得的钝头体壁面温度分布的时间历程。受气动加热的作用，钝头体壁面温度分布逐渐升高，但壁面温度分布曲线之间的距离逐渐减小，表明钝头体壁面温度分布的变化率逐渐降低。实际上当耦合计算时间趋于无穷大时，钝头体壁面温度分布将保持稳定，其本质是通过非定常耦合计算得到了定常耦合分析结果。

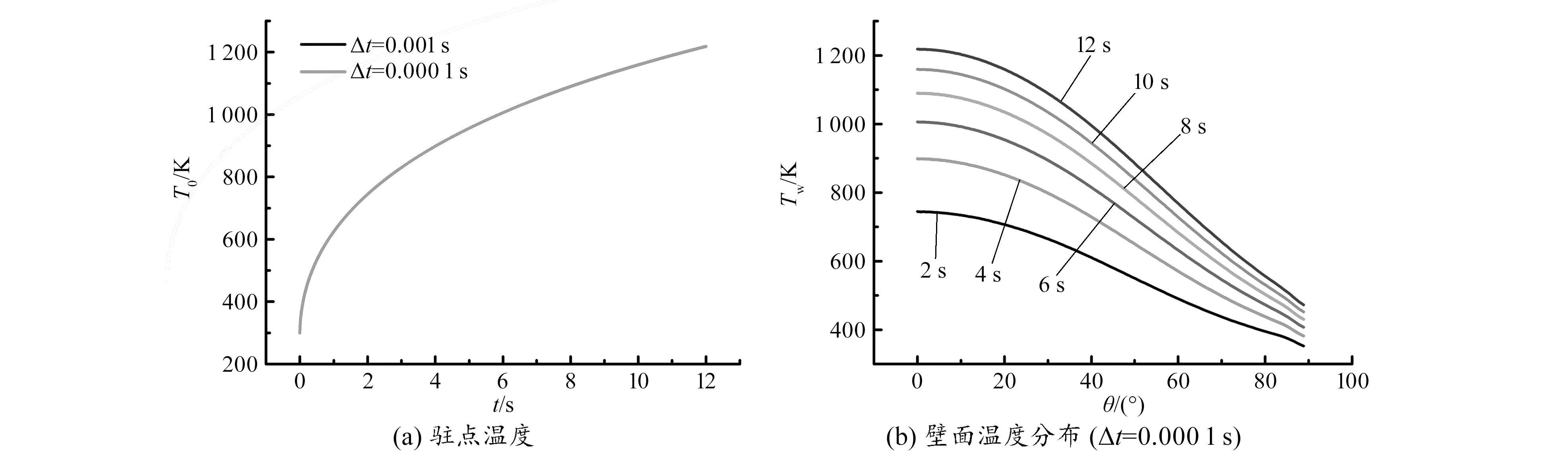
图6 结构驻点温度和壁面温度分布的时间历程

3 结束语

目前广泛采用的高超声速飞行器热环境分析方法未考虑结构温度升高对气动加热的影响，无法准确计算飞行器的结构温度场及评价飞行器的安全性。本文采用一体化耦合分析方法进行了高超声速飞行器气动加热/结构温度场的耦合计算，计算结果充分反映了壁面热流与壁面温度之间的相互影响，是一种有前途的高超声速热环境高精度计算方法。