基于决策树的最优穿越沙漠策略研究

2021-09-15黎金铭潘玉雯阳尚儒

科技经济导刊 2021年24期

黎金铭，毛睿，潘玉雯，阳尚儒

（桂林电子科技大学数学与计算科学学院，广西桂林 541004）

基于特定规则研究穿越沙漠的最优策略，求解在初始点购买资源出发至终点，如何补充资源并赚取更多资金，是研究重点。此课题涉及资源与时间、环境与风险、目标与计划、竞争与合作四项组合优化，通常可用动态规划及启发式算法求解，若将地图简化后建立决策树模型求解，能更好地解决最优策略问题。

1.问题描述

已知未来30 天内的天气或仅知当天的天气，时间最长为30 天或10 天，凭借已知地图(见图1 和图3)，利用初始资金购买水和食物，从起点出发穿越沙漠。途中会遇到晴朗、高温、沙暴三种天气，可在矿山、村庄补充资金或资源，但在村庄资源的价格是起点价格的两倍。目标是在截止期限或之前到达终点，若未到达终点而水或食物已耗尽视为策略失败，到达终点后该活动结束，到达终点时的剩余资金最大。[1]

2.分析问题

穿越沙漠过程中，赶路的资源消耗是停留的2 倍，挖矿是停留的3 倍，每箱水重3 千克，基准价格5 元；每箱食物的质量为2 千克，基准价格为10 元。在图1 地图中每日挖矿收益为1000 元，在图3 地图中挖矿收益为200 元。问题一，已知未来的天气情况，需根据每日天气的变化权衡到底是走是停留还是挖矿，从而到终点时剩余资金最大。问题二，已知当天的天气，但未来天气未知且不会出现沙暴天气，需建立决策树模型，再结合未来天气变化概率进行决策，找出最优赶路方案。

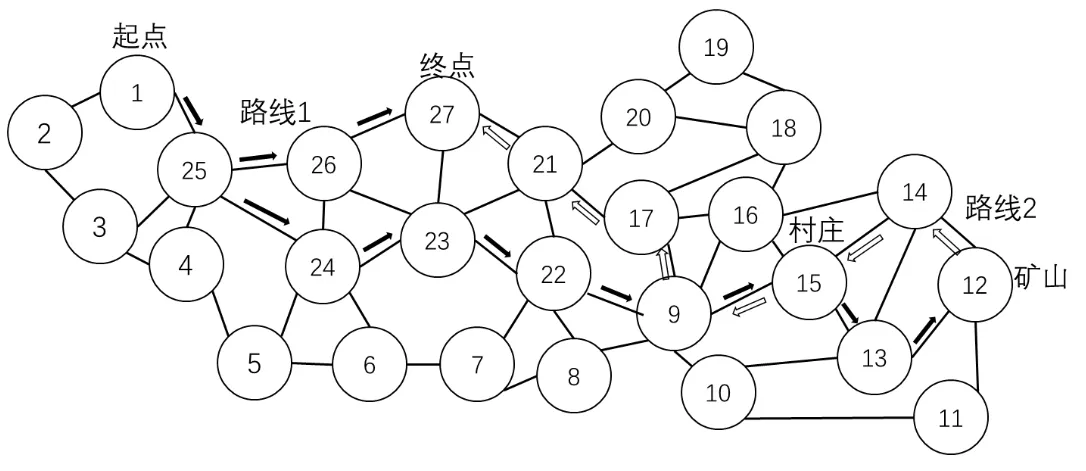
图1 地图1

3.天气条件确定模型的分析与求解

3.1 资源消耗计算模型

根据规则，第i 天消耗资源Qi计算式如下

第i 天补充资源花费QSi=2c1xsi+2c2ysi

xi为第i 天消耗的水数量；yi为第i 天时消耗食物的数量（箱）；c1为水价格；c2为食品价格；xsi表示第i 天路过村庄补给水的箱数，不补充时为0；ysi表示第i天路过村庄补充食物的箱数当不补充时为0；QSi为第i 天在村庄买东所花的资金。第i 天剩余水的数量

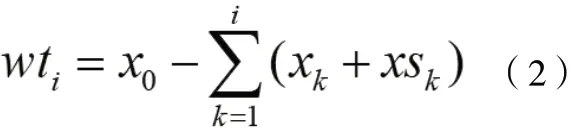
x0为初始购买水的数量，y0初始购买食物的数量。第i 天剩余食物的数量

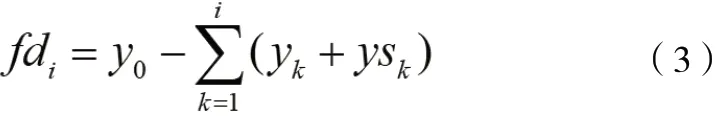
结合公式2、公式3，定义初始时刻负重为M0(≤1200)，初始时刻购买金额为Q0=c1x0+c2y0，由此推导每天负重的公式如下：

第i 天挖矿收益iB当第i 天挖矿收益1000，不挖矿时为0.那么，第i 天剩余资金为

3.2 基于最短路径的决策树模型

如图1 所示，连通两点之间间隔一天的路程。分析地图可知“从起点去矿山不经村庄”花费的时间与“从起点去矿山经过村庄”花费的时间相等同时“从矿山去终点”花费的时间与“从矿山经过村庄再去终点”花费的时间相等。故假设从起点出发经过村庄到达矿山；而从矿山出发去终点经过村庄。根据分析可得到如图2 的决策。

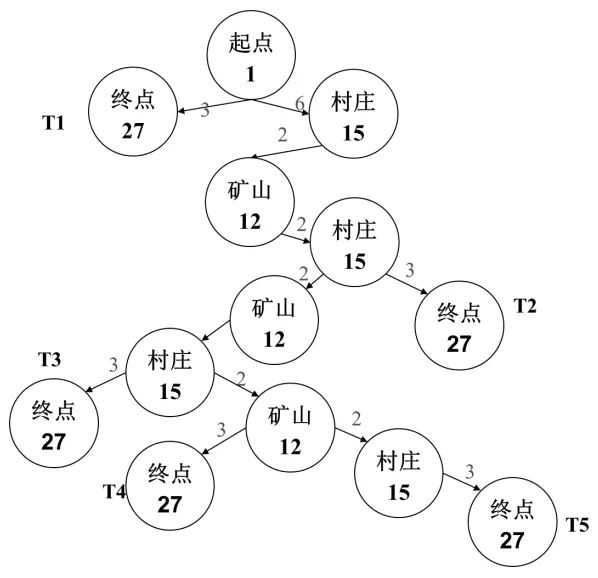
图2 问题一决策树图

3.3 模型的求解

要想到达终点时剩余资金最大需要满足以下条件：一是在矿山挖矿天数尽可能多；二是尽量不在高温天气挖矿和赶路；三是购买的物资满足挖矿和赶路即可；四是在起点购买更多的食物。每日在矿山挖矿的收益为1000 元。假设未来30 天的天气状况已知，基本参数见文献[1]。基于决策树模拟算法的步骤如下：Step 1 输入一月内天气，购买150 箱水、150 箱食物以及决策树路线进行模拟。Step 2 开始模拟路线赶路，碰到沙暴天气停止不动，若是晴朗继续赶路，若是高温可选择停留或者赶路，一天结束计算剩余资金。Step 3 若遇上村庄则去补充资源，补充路上消耗或根据未来天气补充到满足去终点的资源即可。Step 4 碰上矿山，则去挖矿。挖到剩余资源能满足去终点或村庄补充资源停止，直奔终点或村庄。转Step5。Step 5 若能到达终点，重新优化起点背包携带量和村庄补给量，计算最大收益H，进入下一步；否则穿越失败回到Step1，改变高温天气下的决策重现遍历。Step 6 检查决策树图路径，若决策树没有搜索完，返回Step1 按照决策树图重新模拟，计算最大收益Hi与H 比较。若Hi更大则最大收益H=Hi；若路径搜索完输出最大收益H。

表1 问题一每天赶路决策表

由表3 可知，从起点出发，路线1-25-24-23-22-9-15-14-12-14-15-9-21-27，需要赶路24 天，起点购买178 箱水，333 箱食物，经村庄补充163 箱水，只去矿山一次，挖矿7天，再去终点路过村庄补充36 箱水，24 箱食物，最高收益为10470 元。

表3 高温停留和高温赶路的资源花费

4.天气条件未知的模型分析与求解

模型建立和求解：问题二穿越沙漠的范围变小，穿越的时间限制为10 天，仅知当天天气，但不出现沙暴天气，每日挖矿收益为200 元，建立决策树模型分析最优决策，简化后地图如图3 所示，基本参数见文献[1]。由图3 可知，从起点出发去终点的赶路方案仅有两种。

图3 地图2

方案1 在起点处购买资源后开始出发，直奔终点即1-5-6-13；方案2 在起点处购买资源后出发去矿山，在矿山挖矿后，再去终点即1-4-3-9-11-13。方案2 比方案2 多花两天的时间去终点，判断两种方案的优劣，只需计算方案2 矿山挖矿所得最大净收益（挖矿收益减去挖矿时的资源花费）减去2 天赶路的花费是否为正数即可。已知挖矿花费是基础消耗的3 倍，在矿山的最大挖矿时间为5 天。假设挖矿时，天气全为晴朗，计算可知每天挖矿花费165 元，每天挖矿收益200，净收益35 元，5 天的收益175 元，赶路花费220 元。方案(2)挖矿的收益小于赶路花费，说明直奔终点是最好选择。

处于高温天气的赶路方案：假设在赶路过程中，天气变化概率都是独立同分布的，“晴朗天气”每天出现概率为P，则“高温天气”出现概率为1-P，晴朗天气出现次数服从二项分布。

完全不停留决策分析：当天气为晴朗时，资源的消耗最小，最优决策为前往终点。当天气为高温时，是停留还是行仍需讨论。赶路到终点所需时间记为t；可推导t 天时（0≤t≤ 3），赶路的平均资金消耗公式如下：

其中，kt,i为到达终点只剩余t 天路程时，天气晴朗出现i次的平均消耗资金；P 为晴朗出现概率，1-P 高温出现的概率。

权衡原地停留与继续赶路的决策分析：当剩余天数为j 天时，假设当天天气为高温，对应该停留还是赶路进行分析计算。当决定在高温的天气状况中进行原地停留时，资源总花费COST1,j为高温当天的停留资源花费Qstay与剩余j 天预测的赶路资源花费Ej之和；当决定在高温天气赶路时，资源总花费COST2,j为高温赶路花费Qwalk与剩余(i-1)天预测的赶路平均资源花费Ej-1之和；经分析可知当COST1,j＞COST2,j时，应选择停留；当COST1,j＜COST2,j时，最优策略是选择继续赶路；当COST1,j=COST2,j时，赶路或停留皆可。

模型的求解：计算高温天气下的赶路消耗和停留消耗后，再将晴朗概率从0.1 至0.9 进行遍历，最终得到高温停留和高温赶路的资源花费如表5 所示。

由表5 可知当晴朗天气出现的概率在0.85 以下，最优决策是不停留直奔终点；当晴朗天气出现的概率超过0.85，最优策略是原地停留，等待晴朗天气出现再继续赶路。