由爆炸引起的隧道衬砌与土体相互作用机制的数值模拟分析
2021-09-15赵立财吕家栋
赵立财,吕家栋
(1.台湾科技大学 营建工程系,台北 10607,中国;2.中铁十九局集团 第三工程有限公司,辽宁 110136,中国)
埋地衬砌隧道常用于流体物料的运输、贮存、输送等,该类结构在爆炸荷载作用下的动力行为和特性是当前的研究热点问题[1]。隧道腔内一般有一层衬砌层,这使得动力荷载作用下隧道土体与衬砌之间存在相互作用[2],隧道内发生爆炸土体中相对较浅的深度产生的压力波对地表会产生影响[1],最终破坏临近表面建筑设施[3]。因此,有必要分析该类由气体、壳体和土体耦合体系所涉及的复杂动力学问题。模拟该类埋地结构在内部爆炸荷载作用下的动力行为最简单的模型是弹簧路基支护衬砌或具有阻抗型响应的简单路基[4,5]。但这两种模型不能考虑土体介质中的波动对衬砌响应的复杂影响,尤其不适用于衬砌与土体之间存在缝隙的开启和闭合时的情况。部分学者通过解析方法考虑隧道内爆炸引起的压力波对周围土体的影响[6,7],然而,他们大都将土体与结构之间的作用模拟为刚性接触,或将切向接触视为零,这与事实相差较大。在考虑间隙条件和波的传播时,变分-差分结合的数值方法法最适合处理这种复杂的土-结构的边界条件[8]。
隧道爆炸引起的衬砌和周围土体的变形是衬砌和土体之间以及土体中诱发的压力波和自由表面之间的动力相互作用的结果。变形取决于爆炸荷载、隧道的几何形状和深度、衬砌结构和土壤的力学性能。此文通过二次开发的形式考虑在ABAQUS大型商用软件中嵌入变分-差分法,研究了全饱和颗粒土隧道爆破引起的动态变形。隧道衬砌为圆形管片结构,由单个线性的弹性混凝土段(管片)组成。不对爆炸过程建模,其影响通过施加在隧道管片衬砌上的特定压力脉冲来模拟。
本构模型的选择取决于压力幅值,本文采用了有效应力原理和亚塑性模型描述土壤性能。在本文中,为适用于隧道管片衬砌结构,则压力荷载幅值高达15 MPa。在完全饱和的土壤中,这种荷载所引起的有效压力不超过1 MPa。与准静态变形和地震变形等问题相比,高速率荷载作用下的爆破土体变形数值模拟需要更加精细的空间离散化。边值问题空间离散的必要程度取决于解的空间变化。伴随着应力波的反射和相互作用,特别是当孔隙水空化时,具有非线性土壤性能的土体可能会出现奇异性和不连续性[9,10]。即使初始条件和边界条件是连续的,非线性介质的高速率动态变形也有可能在有限时间内导致不连续解(对于压力相关刚度的固体中不连续的形成)。为了获得此文所考虑问题的可靠数值解,网格间距应小至几厘米。在仔细查阅关于爆炸引发的土与结构物相互作用数值研究的文献后,我们发现,特别在研究三维问题时,计算网格往往过于粗糙[11,12],过于粗糙的网格会造成极大的误差。
利用有限元软件Abaqus/Standard将隧道土体相互作用问题转化为二维平面应变问题。虽然二维公式实际对应的是线爆炸源而非点爆炸源,但它可以用精细空间离散化来解决该问题,这使能够在精细网格上获得精确解,并详细分析变形过程。在这个过程中,特别要注意隧道管片衬砌的变形和孔隙水的空化现象。
1 土体的本构模型
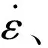
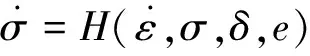
(1)
式(1)在小应力下进行修正,见附录A。该式计算了晶粒间应变
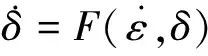
(2)
式(1)、(2)中的函数H和F可在文献[14]或[15,16]中找到。本研究采用的本构参数如表1、表2所示。
从式中可以看出空隙率的变化
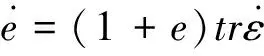
(3)
对不可压缩的固相(颗粒)有效。
在局部不排水的情况下,假定土体渗透率足够低,该问题即可解决。孔隙压力的本构关系为
(4)
除非绝对孔隙压力(包括大气压力)低到足以引起孔隙水的空化,否则饱和土的模量Kf等于纯水的模量Kw=2.2 GPa。此时,孔隙流体体积模量Kf突然降至接近于零的值。假设孔隙水不能承受拉应力,并且忽略空化水中的蒸汽压力,则Kf对压力的依赖关系可以表示为
(5)
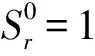
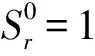

表 1 福建某地区砂的本构参数[17]

表 2 含晶间应变的扩展亚塑性模型的附加本构参数[16]

图 1 孔隙流体压力pf是孔隙流体体积应变εf的函数, 当时,饱和度为Fig. 1 Pore-fluid pressure pf of Volume

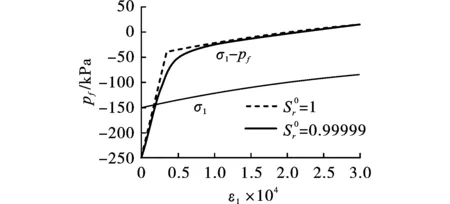
图 2 采用低塑性模型计算饱和土的单轴扩展,初始静水有 效应力为-150 kPa,初始孔隙压力为100 kPa,孔隙率为0.6Fig. 2 The uniaxial expansion of saturated soil was calculated using a low plastic model.The initial hydrostatic effective stress was -150 kPa,the initial pore pressure was 100 kPa, and the porosity was 0.6
2 边界值问题
该问题可转化为图3中的半空间隧道的二维平面应变问题。地下水位和隧道中心分别位于2 m和15 m处。隧道衬砌为圆形结构,内径2.9 m,厚度为0.35 m,由单个弹性混凝土管片组成,如图4所示。在给定摩擦角的情况下,两个筒体之间以及筒体与土壤之间的力由干摩擦产生。套管参数及摩擦角见表3。取零摩擦角的原因是接触面的最大剪应力由土体中的有效正应力决定,而Abaqus用总正应力来计算剪应力。接触算法不适用于非零摩擦建模。而该算法允许土和管片之间存在正常偏差分离,这对解几乎没有影响。
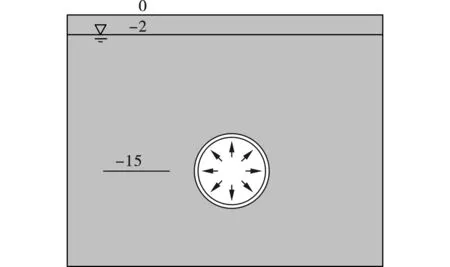
图 3 隧道半空间(单位:m)Fig. 3 Half space of tunnel(unit:m)
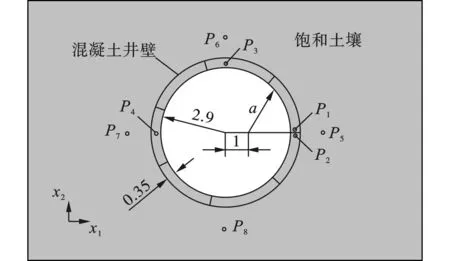
图 4 隧道的横截面(单位:m)Fig. 4 A cross section of a tunnel(unit:m)
土体和隧道管片衬砌的初始应力在重力作用下处于静力平衡状态,在远场处于流体静力状态。初始空隙率e是均匀的,等于0.6,这相当于相对密度为0.77,估计为(ec0-e)/(ec0-ed0),见表1所示。
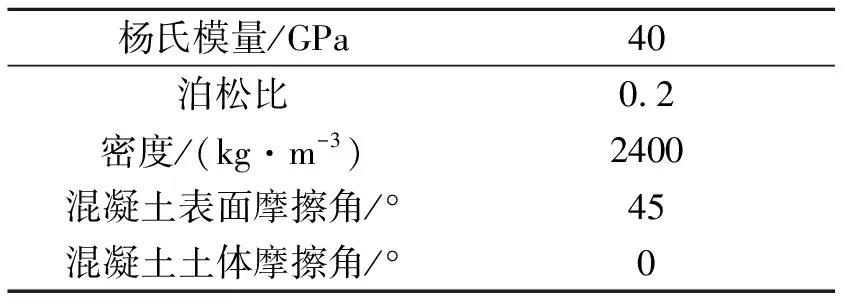
表 3 隧道材料参数
本研究通过对隧道管片衬砌内表面施加一定压力,模拟隧道内爆炸所产生的影响,考虑了两种载荷情况:对称载荷和非对称载荷。对称加载对应于隧道中心的爆炸,衬砌表面各点的边界条件由图5所示函数给出。非对称加载模拟了隧道中的偏心爆炸,衬砌表面某一点的边界条件由f(t-τ)给出,其中f(t)为图5所示的函数,延迟时间[s]为
(6)
式(6)中的距离a,m定义在图4中。同时式(6)表示出衬砌左右两边的加载均延迟了1 ms。
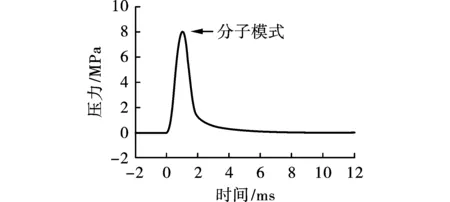
图 5 施加于隧道管片衬砌上的压力Fig. 5 Pressure applied to tunnel lining
隧道中心与计算域外边界之间的距离约为70 m。本研究未使用透明边界,由于只有当从外边界反射的波到达图3所示的隧道周围感兴趣区域时,数值解才有效,所以外边界的边界条件类型并不重要。目前的计算能力仅允许我们模拟高达70 ms的饱和土壤。
边界值问题采用有限单元程序Abaqus/Standard、隐式Hilber-Hughes-Taylor时间积分方案、4节点双线性四边形单元CPE4选择性简化积分求解。衬砌附近的有限元网格如图6所示,时间增量是10-5s。
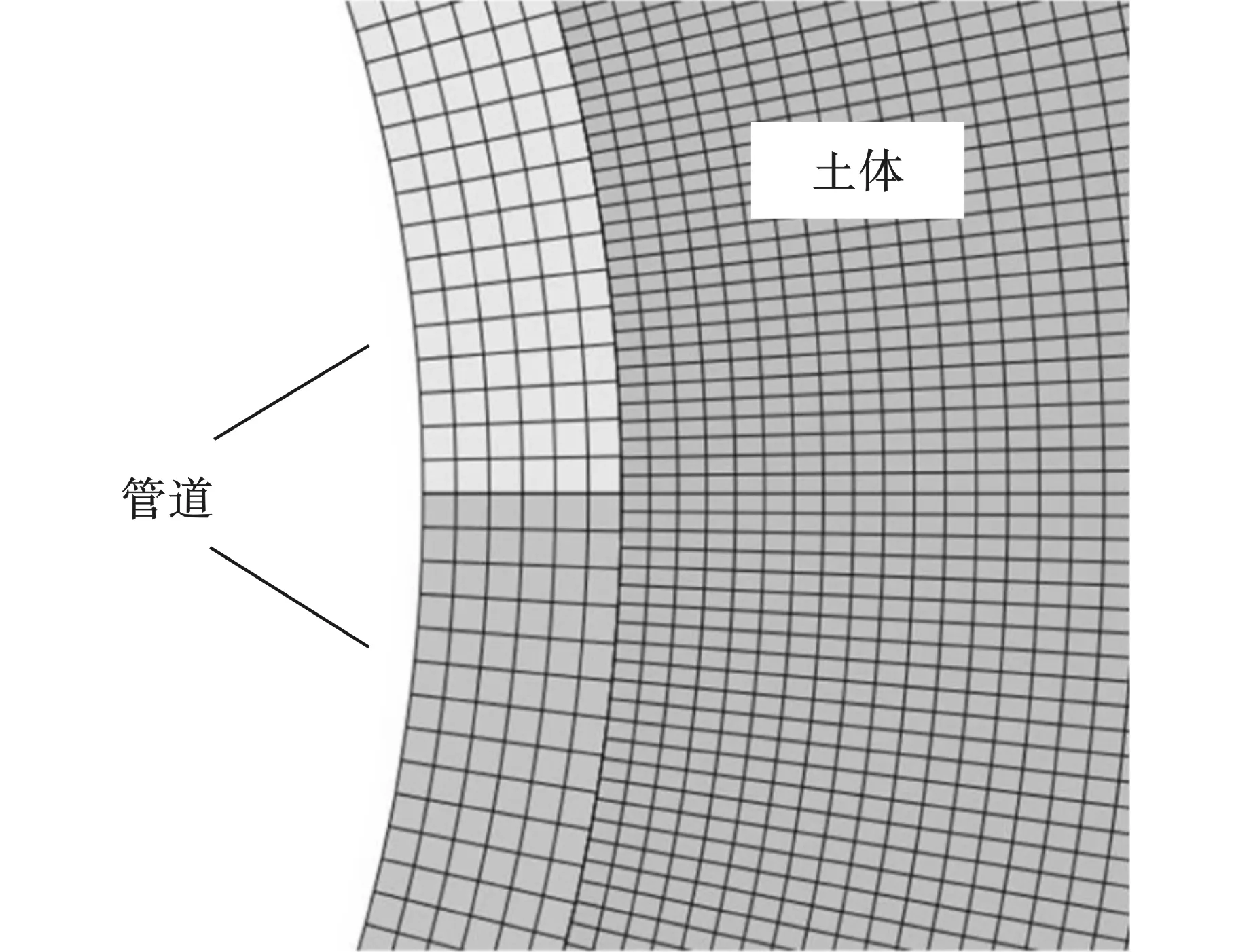
图 6 内衬附近的有限元网格Fig. 6 Lining around the finite element mesh
假设:各向同性线性弹性骨架在局部不排水条件下,并存在单轴压缩。设Δσ和Δσtotal分别为变形引起的轴向有效应力和总应力的增量。然后可以得出
(7)
式中:cp为干骨架的纵波速度;n为骨架的孔隙率;δs为固相(晶粒)的密度;v为干骨架的泊松比;Kf为孔隙流体的体积模量。如果Δσ和Δσtotal分别为平均有效应力和总应力增量,则
(8)
其中
(9)
为干骨架的体积模量。注意,平均应力式(8)不仅适用于单轴压缩,而且适用于任何变形。在完全饱和的情况下,Kf等于纯水的体积模量(2.2 GPa)。如图7所示,由式(7)、式(8)给出的分式为n=0.375,δs=2650 kg/m3,v=0.3时的函数。由图7可知,如果总压力不超过15 MPa,则有效压力在1 MPa以下。
附录A 低塑性小应力矫正
亚塑性下的骨架刚度与(-σ)m近似成正比,其中σ为平均应力,m为常数。可以看出,当0
(10)
式中,参数ζ>1,参考应力σζ<0。若σ/σζ>>1,修正式(10)转变为式(1),当σ→0时,刚度与(-σ)ζ成正比,由于ζ>1,拉应力均值趋近于0。计算中使用的参数为ζ=2,σζ=-1 kPa。
无应力状态下的数值计算难度不仅与低塑性有关,而且与无粘性土模型有关。需要注意的是,式(10)并不是对应力消失的亚塑性模型的全面修正,而是解决一类特定的大膨胀问题的临时工具。式(10)将土体扩展到接近零应力的大变形后压缩到初始密度时,可能会产生过低的刚度。但该缺陷并不影响大膨胀时干土上层的解,因为在考虑的时间内,该层的土壤密度还没有恢复到初始值。
附录B 水气混合物的体积模量
忽略水气界面的毛细压力,由水和自由气体组成的流体体积模量为[10,19,20]
(11)
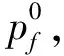
(12)
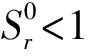
为了在存在不连续和高梯度的情况下获得可靠的数值解,除了本构应力式(1)和孔隙压力外,本研究还引入了粘滞应力σvis。数值解中的总应力是σ,-pfⅠ和σvis的和。粘滞应力被认为是具有两个粘滞系数λ和μ的各向同性流体
(13)
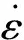
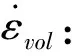
与非空化状态相比,孔隙水空化大大提高了土体的非线性程度,见图1、2中的应变-应力曲线。本构性能的非线性特征在上部干土层中也起着重要的作用。在上土层中应力首先降低到接近零值,然后恢复。如引言所述,在压缩变形率高的复合材料中,非线性应变-应力关系式可能会在解中产生不连续性(激波面)[1,2]。在二维问题中,非线性也可能导致局部奇异点具有高梯度,如图1所示。导致当前问题中不连续性的另一个原因是管片在其反向运动结束时会发生碰撞。但与碰撞产生的冲击波与介质是否是线性无关。不连续问题的数值解需要一种物理或物理阻尼机制,否则解可能会被杂散振荡以致完全破坏。
3 衬砌变形
施加在管片内壁上的压力会导致管片径向移动,并失去接触。接触消失后,这些小管片处于分离阶段,只与土壤发生相互作用。图7展示了图4中四点P1、P2、P3、P4对称加载时管片内水平和垂直位移分量u1和u2。图7(a)中P1和P2点的垂直位移曲线显示,两根管片在1 ms内已经失去了接触。管片之间最大间隙达到3.5 mm。从这两条曲线可以看出,在分离阶段,套管在周向发生高频振荡。振荡以驻波的形式出现,频率为780 Hz。从以下应力曲线也可以明显看出这些振荡。
在分离阶段,管片的径向运动受土壤反应控制。通过土体反应使管体减速,然后向隧道中心相反方向加速,直到它们重新恢复接触,分离期为2530 ms。在此之后,当图7(a)中两条曲线分开时,仍然可以观察到几个短时间分离,这表明管体进一步出现不规则振动。管片在分离阶段的最大径向位移约为4 mm,如图7中虚线所示。
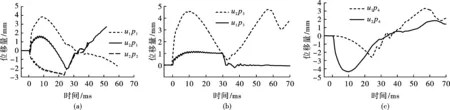
图 7 套管中的位移分量Fig. 7 Displacement component in casing
Abaqus中可用的接触算法可以允许或禁止分离两个物体,这取决于用户的选择。如果允许土与管片之间分离,则管片的高频振动会导致管周围局部分隔带出现和消失,整个管片不会与土壤失去接触。有分离和无分离解之间的差异不显著。
如果隧道位于一个完整空间,衬砌运动迅速衰减后,管片将重新接触。在半空间问题中,从图7可以明显看出,衬砌运动比分离阶段持续的时间长。由位移曲线可知,在30~70 ms这段时间内,衬砌在水平方向上发生变形并向上位移。与全空间问题相比,半空间隧道管片衬砌运动时间更长,其原因是爆轰波与自由表面的相互作用(见第5节)。
图8所示为对称加载时管片内的应力分量。对于图8中点P1、P3、P4,笛卡尔应力分量与管中径向(σrr)或周向(σθθ)应力重合,见图中的符号。只有在运动开始时,由于施加的压力,径向应力才显著增加。周向应力曲线揭示了管在周向方向上的振荡。当能量进入土壤时,振荡减弱。由于这种振荡是以驻波形式出现,所以应力幅值沿管片(沿圆周方向)变化极大,在中间点(如点P4)最大。图8(c)中max表示点P4处最大拉应力为6.5 MPa,为施加压力幅值Pamp的80%,边界条件如图5所示。点P4的最大拉应力σmax与施加压力Pamp之比取决于Pamp。为了发现该相关性,我们使用了不同的Pamp值。结果如图9所示。管片自由表面附近(从点P4向右)的最大拉应力略高于点P4(高达20%)。
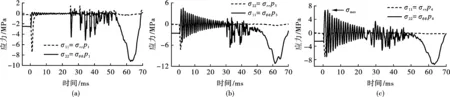
图 8 套管中的应力分量Fig. 8 Stress components in casing
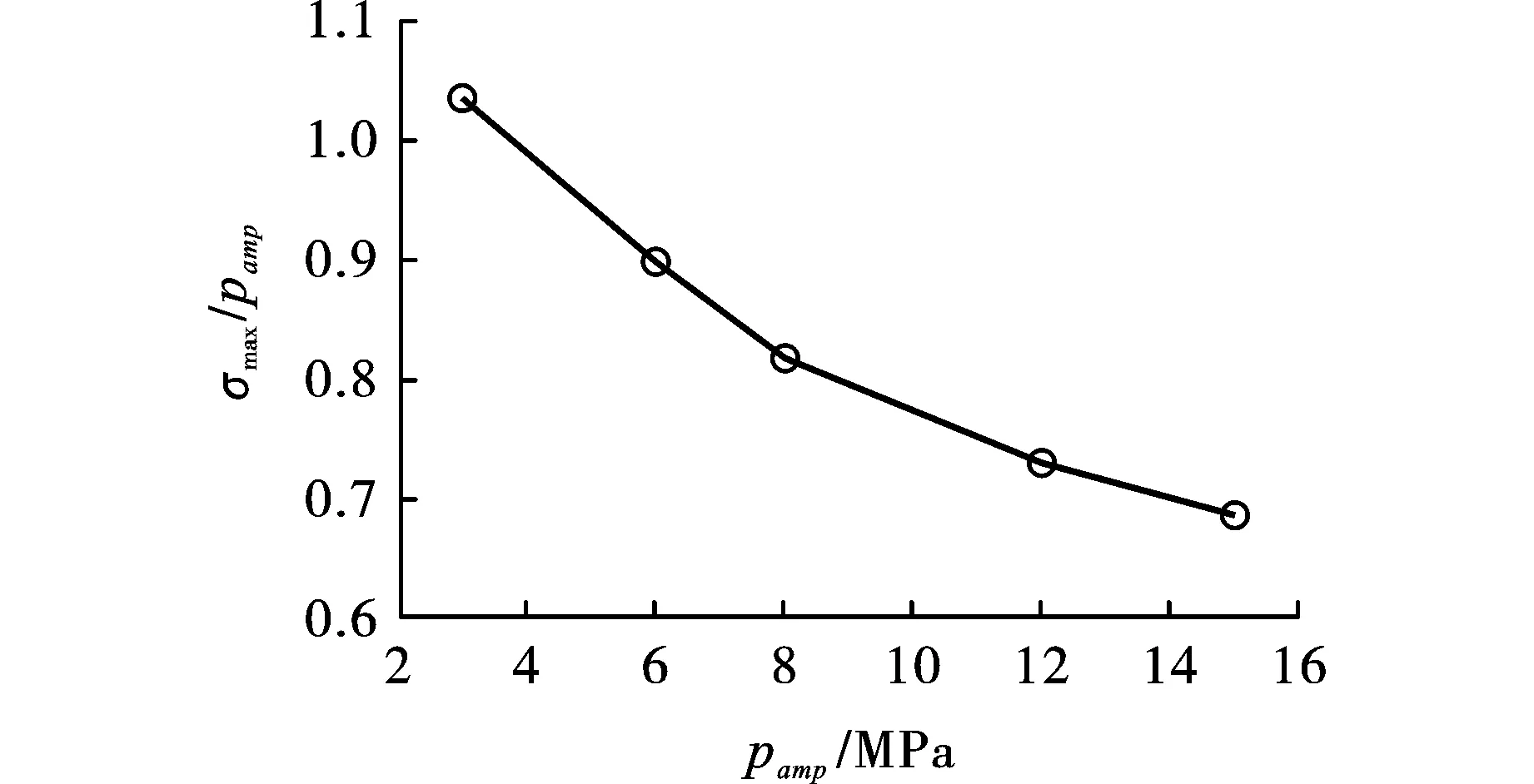
图 9 点P4处的最大拉伸应力σmax [见图8(c)]是施加的压力Pamp的函数Fig. 9 The maximum tensile stress at point P4 [see Fig.8(c)] is a function of the applied pressure
虽然衬砌荷载对称,即同时施加于所有管片,但由于土体刚度随深度变化,土体反力不对称。因此,管片运动也不对称,在分离阶段结束时,管体碰撞不是同时发生,而是在25~30 ms之间按顺序发生。衬砌不对称闭合使周向应力在25~50 ms区间内产生大幅度不规则振荡。在随后的50~70 ms时间内,图8中三种周向应力曲线均表现出较慢的加载-卸载周期,且压应力均为10 MPa,这表明整个衬砌均受到外部压力。从以下对土体变形的分析中,可以明确该压力脉动的原因。对于隧道管片衬砌,该节结果对于式(6)所定义的非对称荷载也成立,两种解之间的差异不明显。
4 土壤变形
施加在隧道管片衬砌上的荷载传递到土壤中会引起压力波。与图5中Pamp相比,管片降低了作用于土壤的最大压力。土-管界面的最大压力约为75%Pamp。爆炸引起的土体变形会导致土体扩展,土体将扩展到足以形成孔隙水空化的区域。由于孔隙水的应变-压力关系近似为一条光滑曲线,如图1所示,因此空穴化过渡也是光滑的,但空穴化定义仍然不明确。为了区分空化水和非空化水,并能够识别空化带,提出孔隙水在孔隙压力pf小于-99 kPa时为空化。图10为对称荷载作用下不同工况下的土体孔隙压力分布。

图 10 孔隙压力在不同时刻为对称加载Fig. 10 Pore pressure is loaded symmetrically at different times
由图10可知,空化开始于隧道周围和上部干土附近两个地方(图10中t=10 ms)。隧道周围的空化现象在6 ms后出现,但在此之前,管片已达到最大径向位移。当压力波(图10中的红色部分,时间为t=10 ms)到达该层时,几毫秒后,靠近上层的凹陷也将发生。爆轰波与地面的相互作用比在弹性半空间中更为复杂。该处我们处理为类似于高压波从水中自由表面的反射。在弹性半空间中,反射波的张应力与入射压力波的张应力大小相同。土中不存在高拉应力,因为无论是骨架还是孔隙水都不能承受该应力。波浪与自由表面的相互作用形成了空化区,使得土体急剧压缩。
隧道周围和上层附近的两个空化区尺寸增大,直至合并在一起(图10中t=20 ms)。在分离阶段结束时,管片碰撞使管片和邻近土壤的径向运动停止。这就产生了一种压力脉冲,该压力脉冲从衬砌传播到土壤中,并将孔隙水压缩到非空化状态。同时空化区的上边界向下移动,导致空化区收缩(t=32和36 ms)。空化区的封闭十分复杂,在空化区边界处存在一个非线性应变-应力关系(见图1和图2)。特别是图10中t=50 ms时,封闭的最后阶段,窄空化区末端存在高压梯度的奇点。图11为图10所示区域A(6.0 m×4.2 m)空化区左侧的平均总应力,时间为t=50 ms。图11中也是有限元网格。由于具有良好的空间离散性,数值解能准确再现高梯度。
空化区最终闭合产生压力突变,形成压力高达1 MPa的扩展高压区(图10,t=58.5 ms)。这样就产生了两种压力波,一种向上传播,另一种向下播。向上传播的波与原爆压波以相同方式从上层土体中反射,产生一个新的更小的空化区,向下传播的波通过隧道。如图8所示,正是这种压力波使隧道管片衬砌变形,并在50~70 ms内增加了套管的周向应力。

图 11 空化区附近(图10 A区域t=50 ms) 的平均总应力和有限元网格Fig. 11 Mean total stress and finite element mesh near cavitation zone
为了进一步研究土体中应变和应力的时间依赖性,本研究仔细观察了距离隧道1 m处的四个点P5、P6、P7、P8,见图4。对称加载时,四点处的体积应变如图12所示。爆炸诱导的压力波首先产生一个较短的压缩-扩展循环,然后产生一个较长的扩展-压缩循环。后者与对应点的空化相吻合。点P7处的应变分量如图13所示,它们揭示了垂直方向(相对于隧道的周向)的拉伸-压缩循环和水平(径向)方向的联合变形,即在空化阶段由爆炸载荷引起的压缩和随后的拉伸-压缩循环。ε12变化表明变形张量的主轴发生了旋转,使得变形路径相当复杂。变形路径如图12和图13所示,如果压缩和拉伸足够大,最终会导致有效压力降低。残余有效压力除载荷幅值外,还与骨架的本构性能、孔隙流体的可压缩性和初始应力状态等因素有关。例如,文献[2]中给出的结果表明,由于高孔隙流体压缩性在孔隙水中存在少量游离气体。因此,一个更大的应变在压缩阶段可能导致剩余有效压力消失,即瞬时土壤液化。当有效压力较初始状态大幅降低时,由于超静孔隙压力耗散,可能会出现应力重分布的准静态变形。在该情况下,有效压力在70 ms后降低到初始值的55.75%,并继续下降,如图14所示。
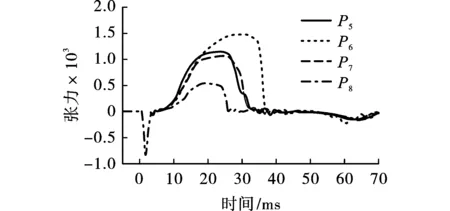
图 12 土壤中的体积应变Fig. 12 Volumetric strain in soil
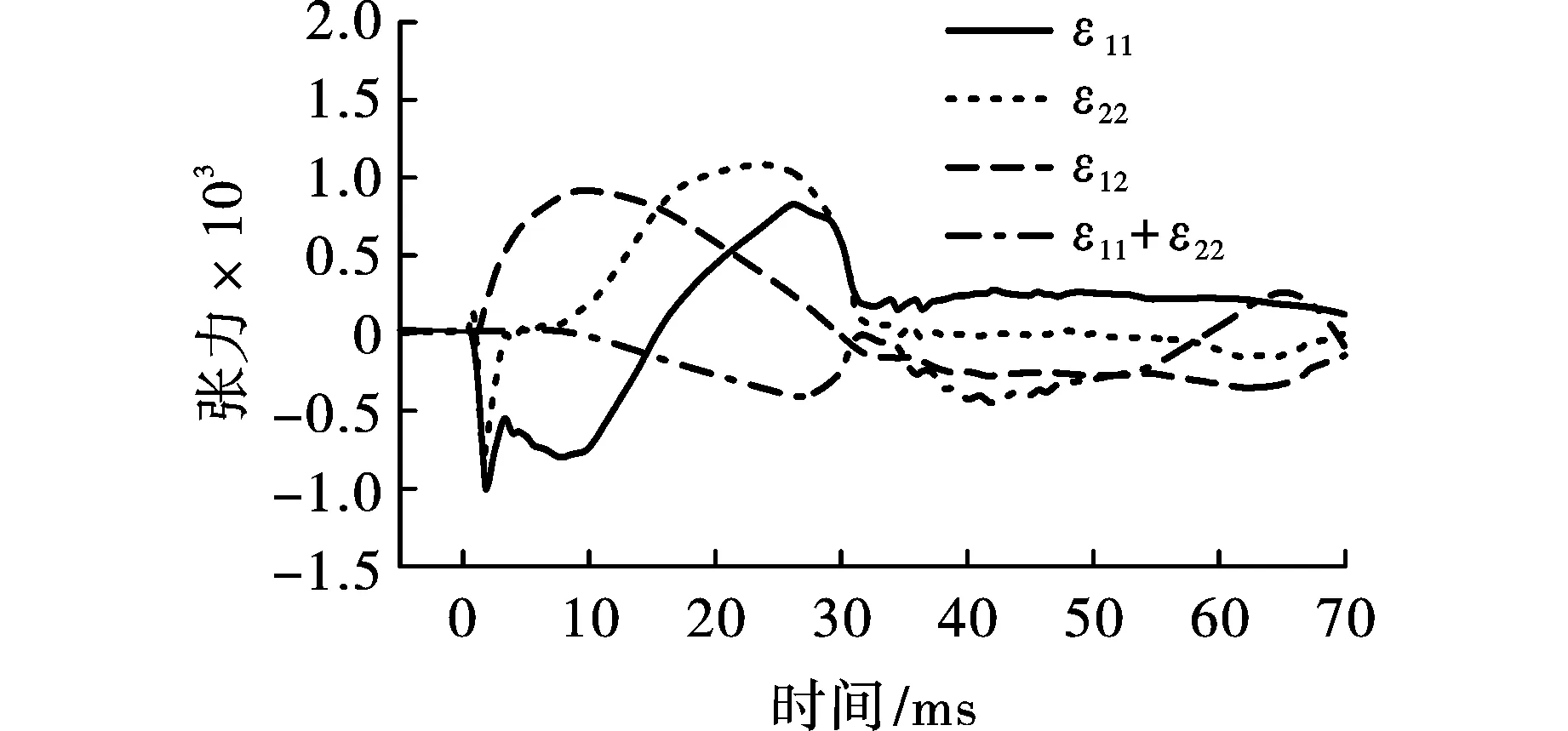
图 13 点P7处的应变分量Fig. 13 The strain component at point P7
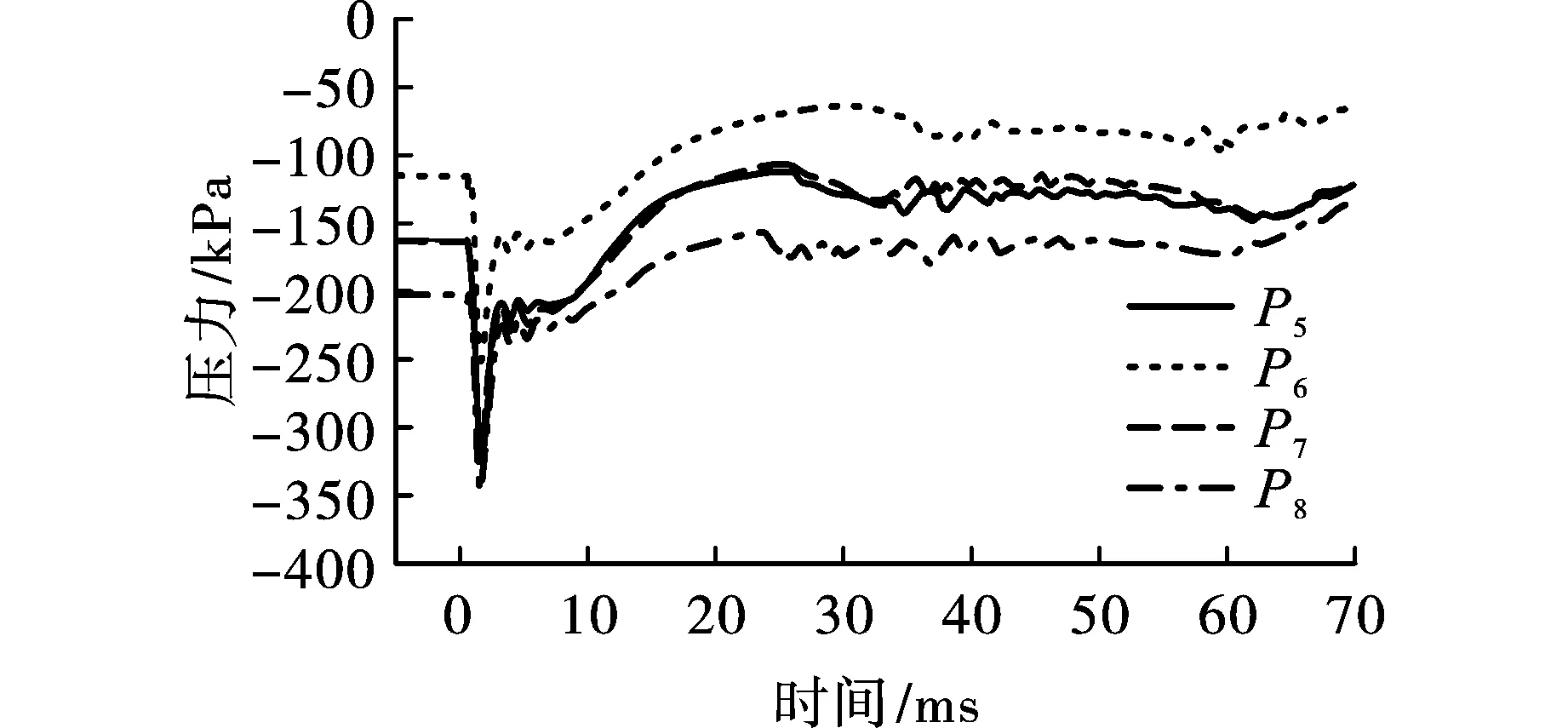
图 14 平均土壤有效应力Fig. 14 Mean soil effective stress
由式(6)定义的非对称加载在解决方案中不会产生任何显著差异。如图15所示,空间分布变得稍微不对称。点P5、点P6、点P7、点P8的应变和应力曲线与图12和图14相似。
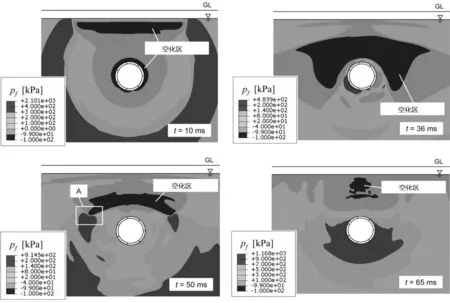
图 15 非对称加载时不同时刻的孔隙压力Fig. 15 Pore pressure at different times under asymmetric loading
土体和衬砌的动态变形在被本数值解覆盖70 ms后并没有结束。在气穴区和上部干层,膨胀土的整体刚度较低,从而阻碍了该过程。70 ms后,地面还没有达到最大垂直位移,并继续向上移动,如图16、图17所示。然而,后面时间内没有显著的压力变化。
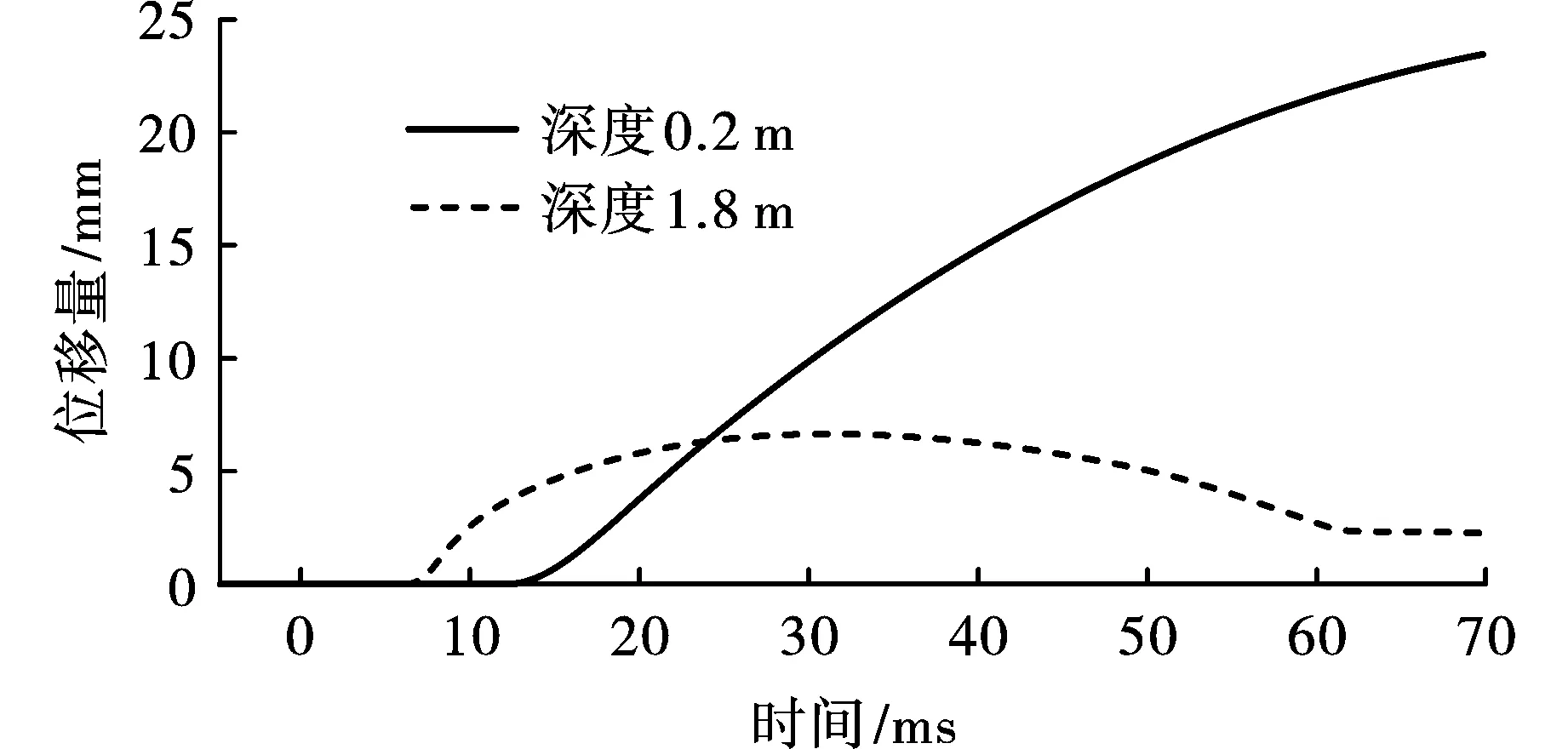
图 16 在隧道中心上方干土上层的两点处垂直位移Fig. 16 Vertical displacement at two points on the upper layer of dry soil above the center of the tunnel
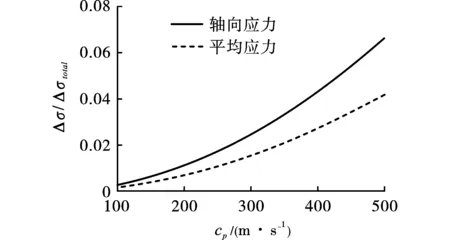
图 17 饱和弹性土单轴压缩时有效应力增量 与总应力增量之比(Cp是干骨架的纵波速度)Fig. 17 Effective stress increment and total stress of saturated elastic soil under uniaxial compression
5 结论
利用Abaqus/Standard模块,基于有效应力原理和亚塑性模型,研究了由隧道爆炸引起隧道衬砌与土体相互作用过程中全饱和颗粒土动态变形特性,并得出以下主要结论:
(1)爆炸过程中的隧道主要表现为径向振动,该过程受土体运动影响显著,主要表现为隧道与土体接触与分离两个阶段。当土体与隧道接触时,土体与隧道之间产生压力,该压力使得隧道径向向内变形,此时土体运动减速。当土体与隧道接触压力达到最大值后,两者开始分离,此时土体径向向外加速运动,直至脱离接触。
(2)爆炸不仅会使得隧道与土体产生变形,还会改变土体孔隙水空化程度和土体弹性模量。隧道与土体在接触与脱离的反复过程中,孔隙水从空化状态与非空化状态之间转变。土体受力状态在拉伸和压缩过程中呈高度非线性关系转换。在气蚀区收缩和最终关闭期间,该非线性会在水气混合物溶液中产生高梯度和奇点。高梯度需要精细的空间离散化才能在数值解中得到精确再现。
(3)对称荷载作用下的土体反力不一定对称,这导致了不对称的隧道管片运动。这种不规则运动会进一步导致隧道体的显著震荡。因此在考虑隧道动力设计问题时,即使对称荷载设计条件下,依然需要考虑远场土对隧道体的影响,因此今后有必要对这一问题进行改进,如采用2.5维有限元-匹配层数值模拟技术进一步研究。
