接触参数对储能飞轮转子碰摩行为的影响
2021-09-15贾翔宇汪军水
贾翔宇,汪军水,徐 旸,张 剀
(清华大学工程物理系,北京 100084)
具有大容量、高效率、高可靠性[1]等特点的电力系统飞轮储能技术,是当前电力电子技术的研究热点之一。近年来,随着复合材料技术、磁悬浮轴承技术和电机及其控制技术[2]的发展,飞轮储能技术取得了快速进步。目前,飞轮储能技术的关键设备——储能飞轮的结构设计和制造主要存在两条技术路线[3]:一是采用高强度合金钢[4]为转子材料的中低速储能飞轮,转速通常在3000~8000 r/min,储能量最大可达60 MJ[5];二是采用复合材料[6]的高速储能飞轮,转速通常可达15000 r/min以上,储能量最大可达到90 MJ[7]。
通常,飞轮转子正常运转时,其轴颈与保护轴承内圈(下文称“定子”)之间不会发生接触。但是,当转子受到扰动或外来冲击后,其与定子间将可能发生碰摩,而随着碰摩的持续和发展[8],系统可能发生运动失稳,严重时将引起轴系损毁,造成运行事故。
转子系统碰摩是典型的非线性动力学问题。张小章等[9]的研究结果表明,碰摩时接触参数——即接触刚度和摩擦系数与碰摩行为的发展及其对系统稳定性的影响有关。戴兴建等[10-12]建立了带有限位器的柔性支承转子系统动力学模型和试验系统,分析并总结了与限位器碰摩时转子响应行为的主要特点。白宇杰等[13]通过柔性支承-刚性转子系统碰摩试验,认为碰摩引起的失稳行为的主频率与接触刚度有关。许斌等[14]和徐尉南等[15]通过解析法分别对Jeffcott转子系统和柔性转子-柔性定子系统的同步全周碰摩行为进行了分析,结果表明接触刚度和转子的不平衡量对稳定性的影响不大,而摩擦系数和外阻尼分别是系统的不稳定因素和稳定因素。
为了保证转子系统受到扰动时的稳定性,本文考虑利用转子碰摩时产生的摩擦力,在有限次碰撞内耗散扰动动能,使系统回到扰动前正常运行的状态。通过数值求解不同接触参数下转子的碰摩行为,得到了碰摩过程中接触参数对系统稳定性的影响规律,为摩擦副材料的选取和接触参数的设计提供了依据。
1 描述转子碰摩的数学模型
为分析飞轮转子碰摩时的共性特征,将其简化为如图1所示、刚度和阻尼系数分别为k和c的两自由度弹簧-阻尼转子系统;其中,质量为m、轴颈半径为R、质心偏心距为e的转子以角速度ω绕点O2匀速旋转。转子与定子间的初始半径间隙为r0,即定子半径Rout=R+r0。以定子中心O1为原点建立平面直角坐标系O1xy,设点O2的坐标为(x,y),根据牛顿第二定律,得到转子的动力学方程
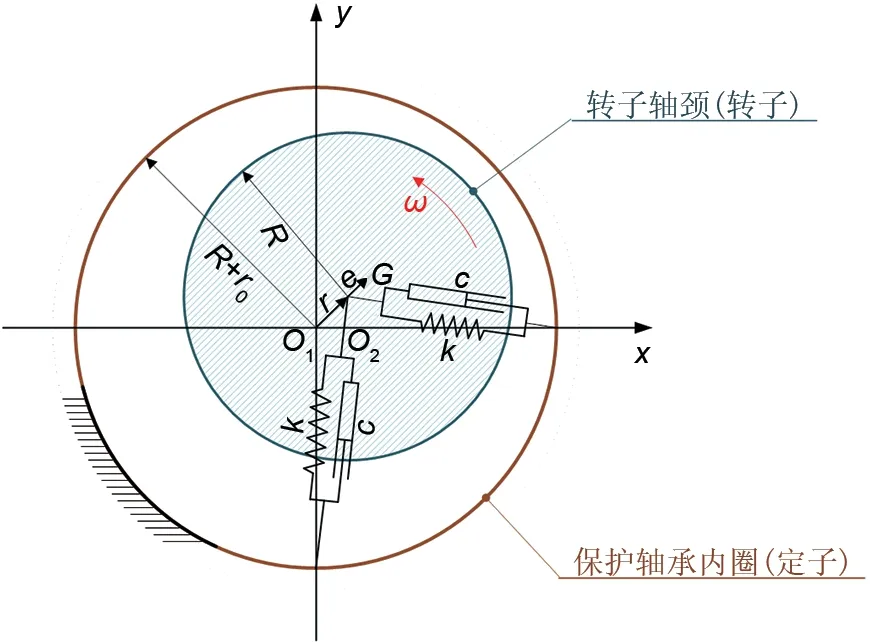
图1 转子系统示意图Fig.1 Schematic diagram of the rotor system
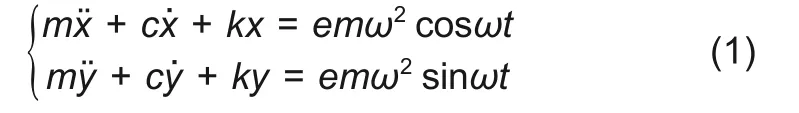
当转子与定子之间发生碰摩时,假设定子的表面硬度比转子支承刚度大几个数量级,且碰摩过程中定子不动,转子转速不变。利用碰摩力模型对方程(1)进行修正:设转、定子发生碰撞时,触点的接触刚度为kb,摩擦系数为μ;当O2的位移r和转子在触点处的法向速度vn满足条件
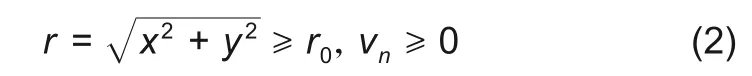
时,接触项被激活;此时式(1)转换为
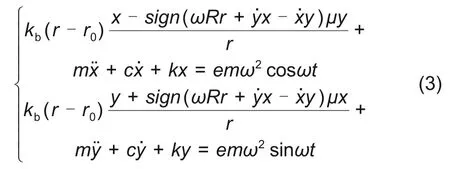
其中,符号函数
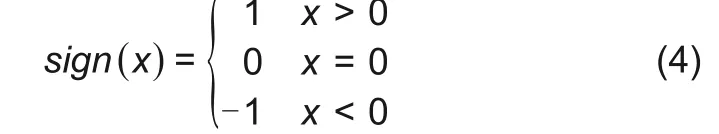
利用四阶龙格-库塔直接积分法数值求解式(1)和(3)。以x方向为例,由于方程阶次为2阶,令
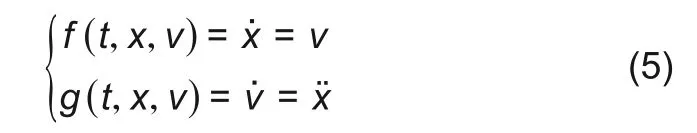
设时间步长Δt=tn+1−tn=h,令hꞌ=h/2,计算
k1=f(tn,xn,vn),l1=g(tn,xn,vn),
k2=f(tn+h′,xn+h′k1,vn+h′l1),
l2=g(tn+h′,xn+h′k1,vn+h′l1),
k3=f(tn+h′,xn+h′k2,vn+h′l2),
l3=g(tn+h′,xn+h′k2,vn+h′l2),
k4=f(tn+h,xn+hk3,vn+hl3),
l4=g(tn+h,xn+hk3,vn+hl3)
得到
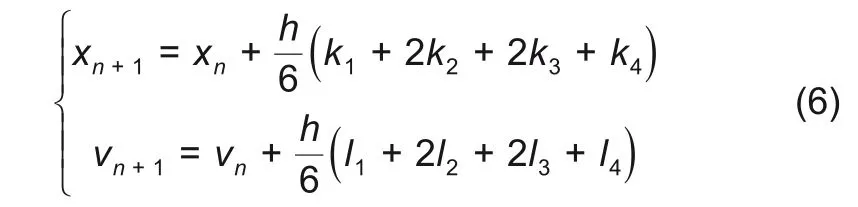
式(6)即为x方向的离散格式;类似的,可以得到y方向的离散格式。下文将使用得到的离散格式,求解转子的动力学行为。
2 转子的碰摩行为
基于前文分析得到的动力学方程的离散格式,本节计算得到了不同数值组合的接触刚度kb和摩擦系数μ下转子的碰摩行为。设置系统参数如表1所示。
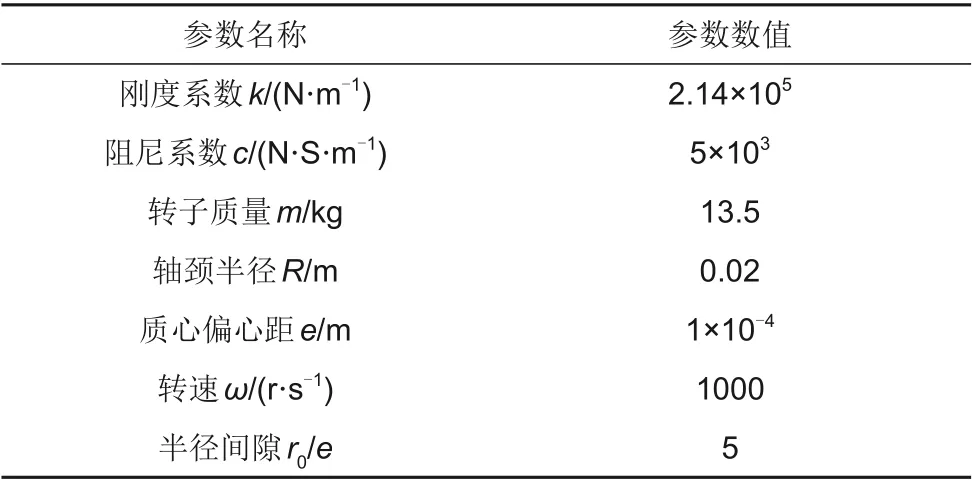
表1 系统参数设置Table 1 System parameters setting
设置计算总时间Ttotal=1 s,时间步长h=Δt=1×10-5s。按照转子稳定进动时的速度关系设定初始条件,即
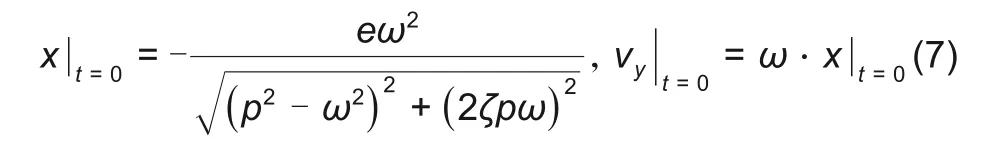
其中
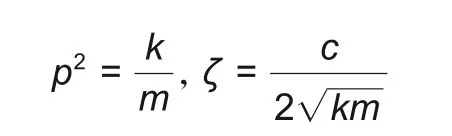
未对转子施加扰动时,转子轴颈中心(下文称“转子中心”)的运动轨迹和对应的FFT曲线如图2所示。从图2可以看出,正常运行时转子除自转外还绕着原点作同步正进动,进动的频率为离心力的激振频率,即自转转速。此时,转子中心偏离原点的位移在半径间隙内,即转子与定子之间不发生碰摩。
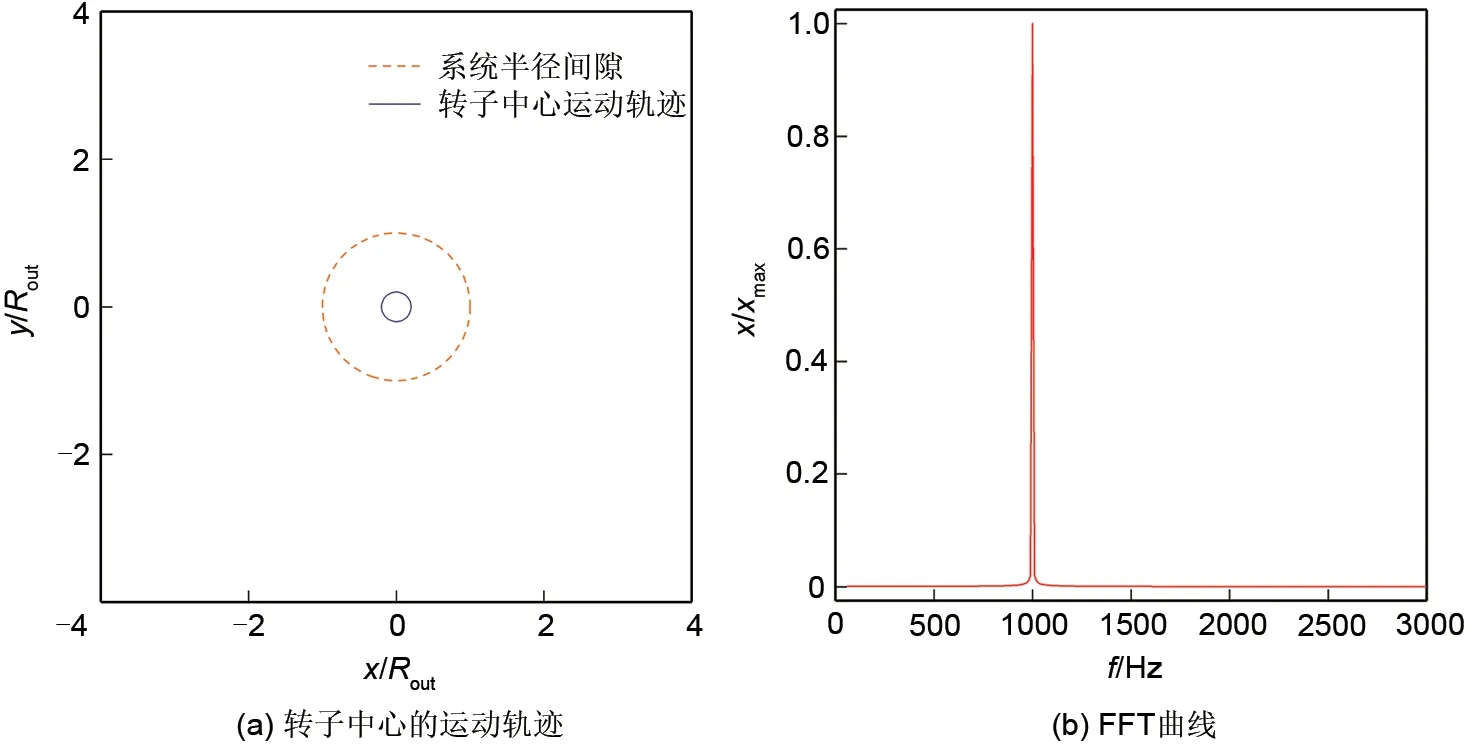
图2 无速度扰动时转子中心的运动行为Fig.2 Motion behaviors of rotor center without speed disturbance
激活碰摩项并改变计算参数。在t=0.3Ttotal时刻对转子施加大小为δvn=αvpR的法向速度扰动,其中速度扰动系数αv=0.1。接受扰动后,转子存在下述三类碰摩行为。
(1)受到扰动的转子偏离稳定运动轨迹,与定子发生碰摩;转子中心的轨迹出现“花瓣形”的Hopf分叉。经过若干次碰摩之后,速度扰动带来的动能总可以在剩下的0.7 s时间内完全衰减,转子中心的运动将回归到稳定运动轨迹,如图3和图4所示。
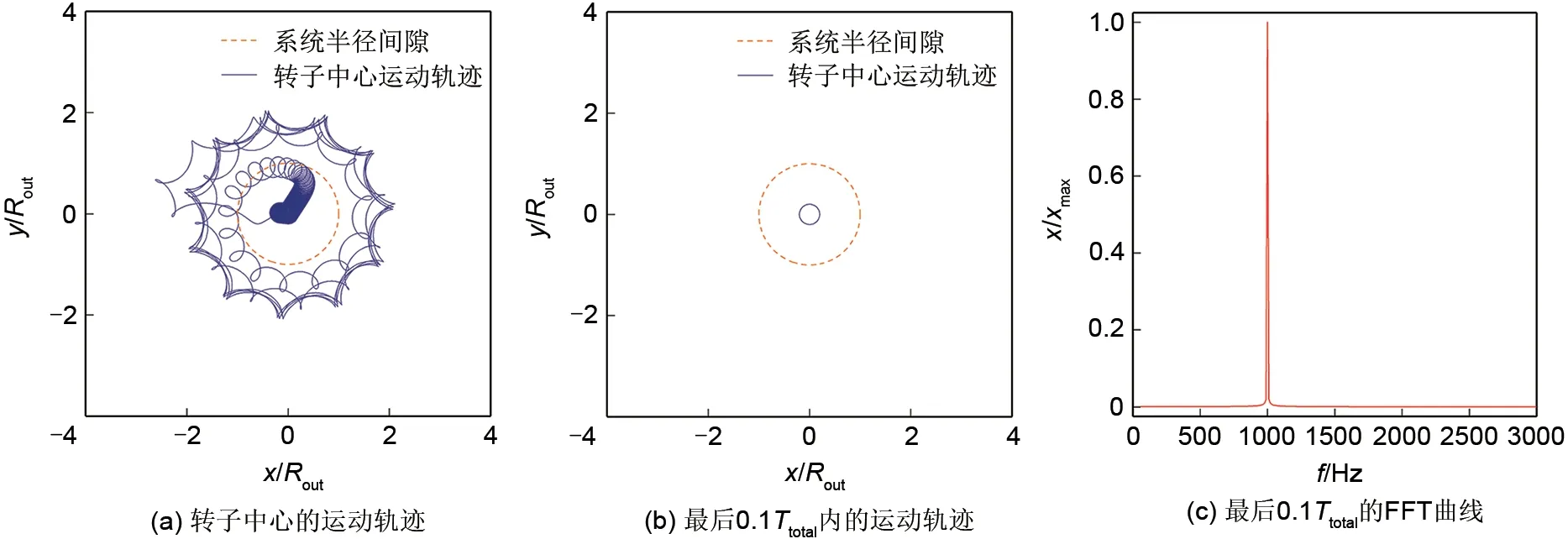
图3 经过碰摩,转子中心的运动回归稳定状态(kb/k=1×102,μ=0.7)Fig.3 Rotor returns to stable after collisions(kb/k=1×102,μ=0.7)
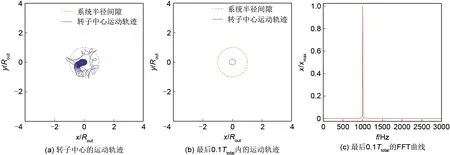
图4 经过碰摩,转子中心的运动回归稳定状态(kb/k=1×104,μ=0.34)Fig.4 Rotor returns to stable after collisions(kb/k=1×104,μ=0.34)
(2)受到扰动的转子与定子发生不停碰撞,碰撞过程中的最大位移和形变没有明显衰减,且0.7 s的时间不足以使这种碰撞停止,如图5所示。从FFT曲线中可以看出,除了激振频率成分外,转子的运动还存在着大量无规则的低频成分;即此时激振频率不再是唯一的主成分。
(3)受到扰动的转子,其稳定运动轨迹冲出半径间隙并稳定在某一位置,此时转子与定子发生全周碰摩,且低频成分的幅值和比例进一步增加,如图6所示。
以上三种动力学行为中,图5和图6对应的不停碰撞和全周碰摩即为两种失稳类型。对于飞轮系统而言,失稳现象不仅可能引起不规则振动和噪声,还可能造成转子与定子之间不可恢复的磨损,甚至是转轴的永久性弯曲和轴系损毁。因此,失稳是实际工况下需要避免的情况。
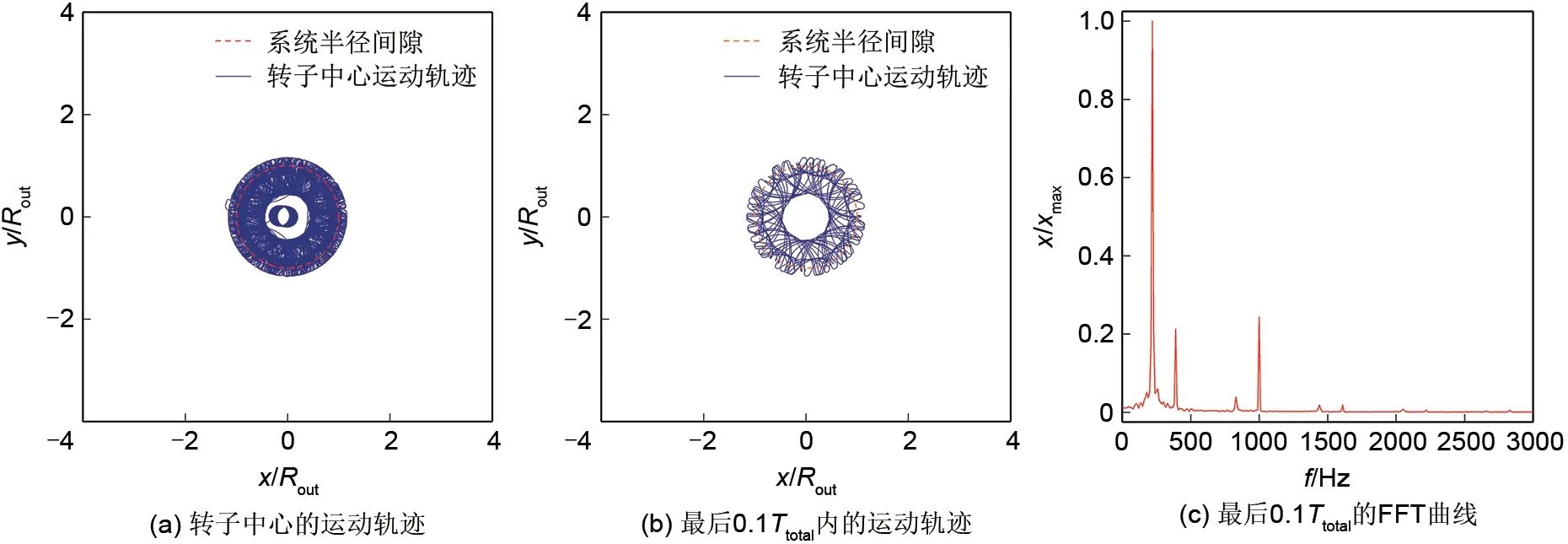
图5 转子与定子不停发生碰撞(kb/k=1×104,μ=0.35)Fig.5 Rotor and stator collide continuously(kb/k=1×104,μ=0.35)
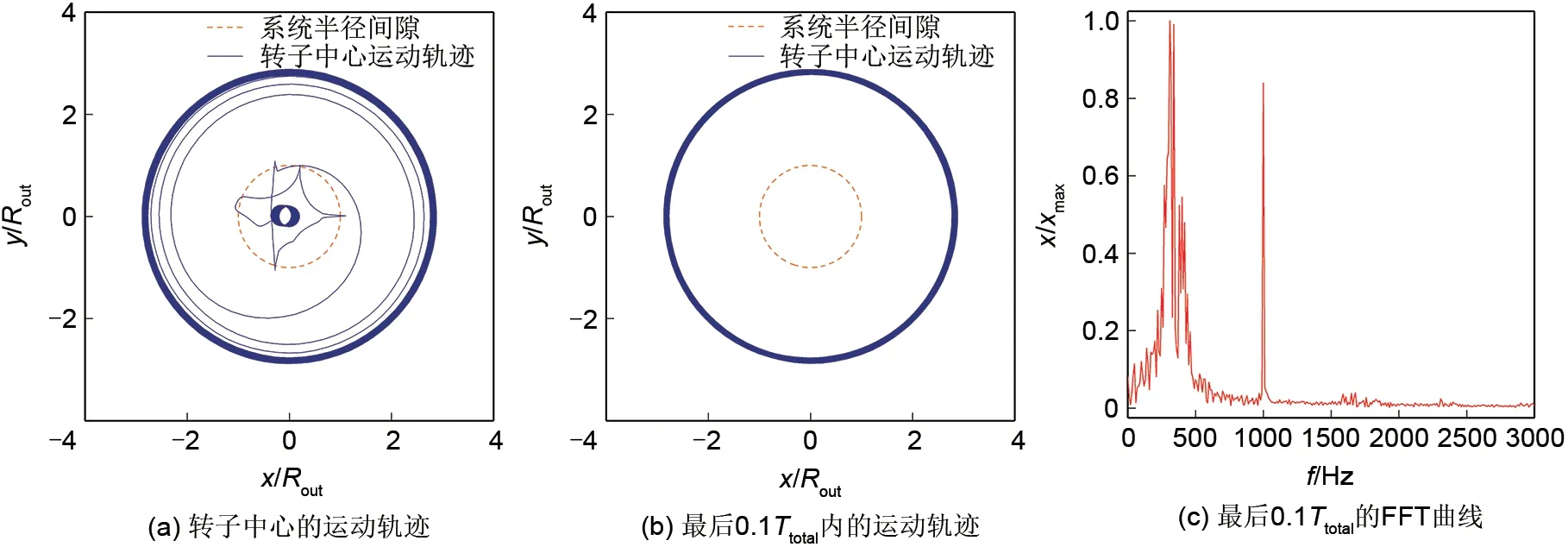
图6 转子与定子发生全周碰摩(kb/k=1×106,μ=0.4)Fig.6 Rotor and stator rub against the entire circumference(kb/k=1×106,μ=0.4)
3 接触参数对转子碰摩的影响
从第2节中可以得出,若某些因素的作用对正常运转的飞轮转子产生了扰动,可以利用碰摩过程衰减扰动动能,使系统回到稳定的运行状态,进而达到增强系统稳定性的目的。但是,如上文所述,在设计转子与定子之间的接触参数时,需要考虑并避免系统失稳的情况。
在表1给定的系统参数设置下,设定接触刚度kb/k=1×104;设置摩擦系数的计算步长Δμ=0.01,计算摩擦系数取值在0.0≤μ≤1.0区间内的转子运动行为,得到对数坐标下碰摩总次数N碰撞随摩擦系数μ的变化曲线如图7所示。从图7中可以看出,当摩擦系数μ处于区间0.00≤μ≤0.34内时,受到扰动后的转子经过碰摩后总能回到稳定状态,且碰撞总次数满足N碰撞<1×102,并随摩擦系数μ的增大总体呈现出先下降后上升的趋势。N碰撞取最小值时对应的摩擦系数,即kb=1×104k时摩擦系数的最佳取μ最佳落在子区间0.05≤μ≤0.15内。重新设置步长Δμ=0.001,计算得到μ最佳=0.104。当μ≥0.35时系统发生失稳;μ≥0.372时发生全周碰摩现象,定义此摩擦系数为该接触刚度下的临界摩擦系数μ临界=0.372。综上所述,当kb=1×104k时,摩擦系数的取值范围为0.00≤μ≤0.34,最佳摩擦系数μ最佳=0.104。
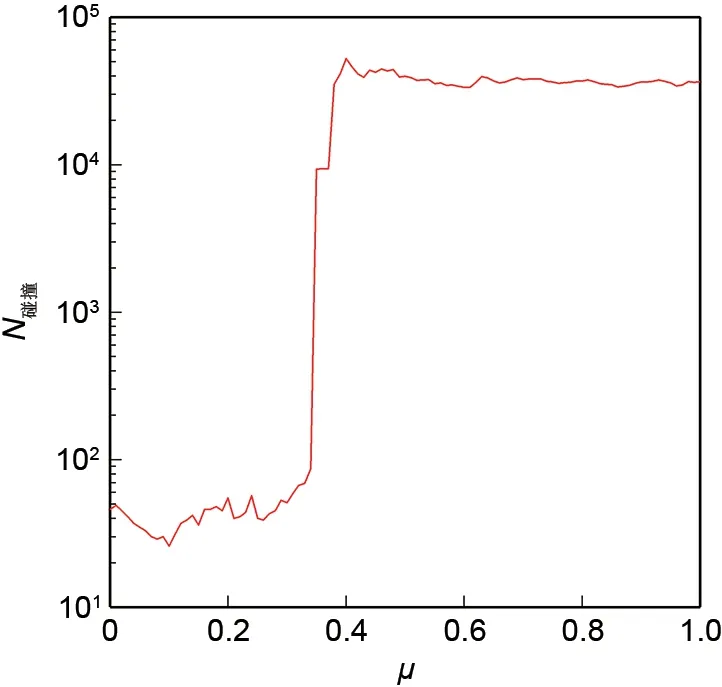
图7 碰摩总次数N碰撞随摩擦系数μ的变化曲线(kb/k=1×104)Fig.7 Curve of N碰撞with increasing ofμ(kb/k=1×104)
保持表1中的参数不变,改变接触刚度kb的取值,分别计算不同kb下总碰撞次数N碰撞随摩擦系数μ的变化,如图8所示。从图中可以看出:①当kb/k=1×101以及kb/k=1×107时,N碰撞随μ的增加基本保持不变,μ在全区域0.0≤μ≤1.0内取值都可以使系统回归稳定。总体而言,kb越大,接触碰摩时正压力、摩擦力越大,扰动动能衰减越快,系统稳定性的提升越明显;②当kb/k=1×102~6,即多数实际飞轮系统中转子和定子接触刚度的取值时,落在区间0.00≤μ≤0.20内的μ总可以有效衰减扰动能量并使系统回归稳定;即μ最佳落在区间0.00≤μ≤0.20内,并随着kb的增大而减小,如图9所示;③如图9所示,当kb/k=1×102~6时,均存在一个使系统恰好发生全周碰摩的临界摩擦系数μ临界,并随着kb的增大而减小。当摩擦系数超过μ临界后,大摩擦系数都会诱发系统的全周碰摩等失稳情况,即摩擦系数不是越大越好。
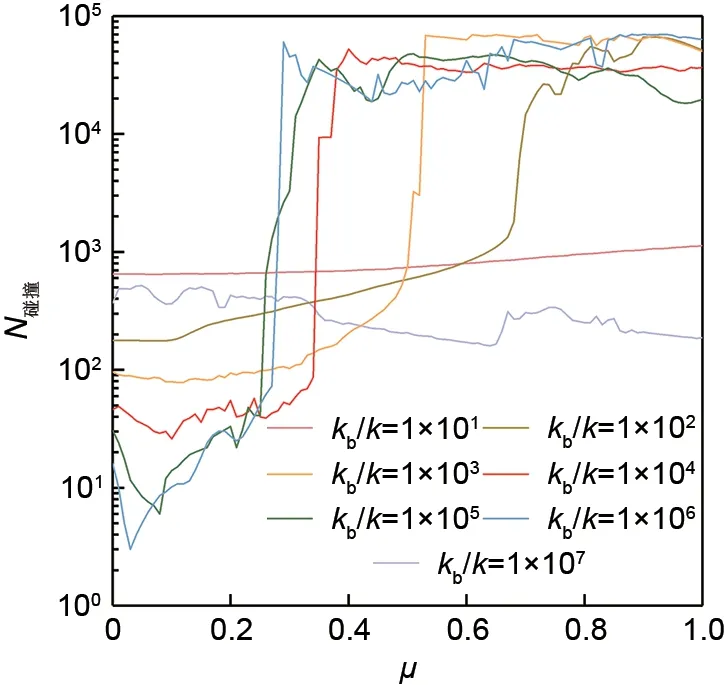
图8 不同kb下,N碰撞随μ的变化曲线Fig.8 N碰撞withμunder different kb
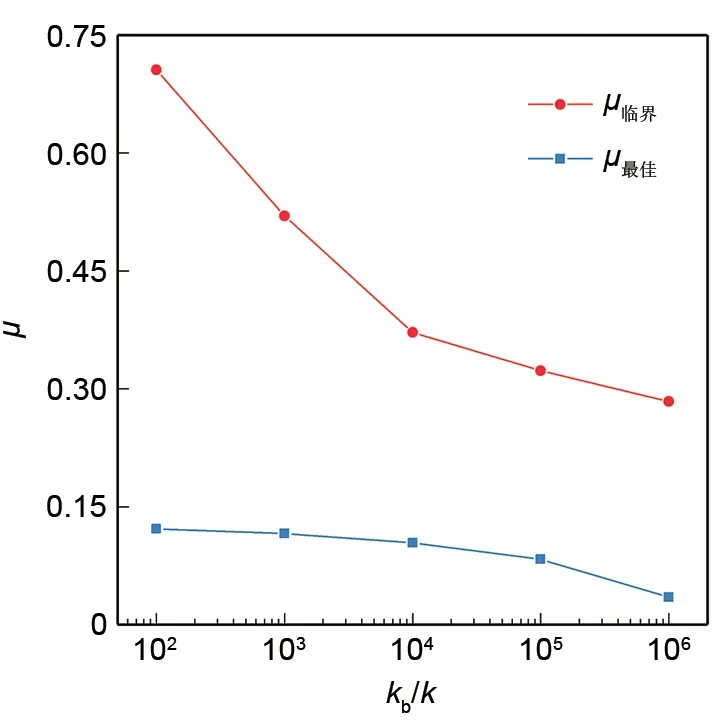
图9 μ最佳和μ临界随kb的变化Fig.9μ最佳andμ临界with different kb
改变系统的阻尼系数,设置c1=0.1c重新计算,得到不同kb下N碰撞随μ的变化曲线以及μ最佳、μ临界随kb的变化曲线,分别如图10和图11所示。从图中可以看出,对于接触刚度较小(kb/k=1×102~4)的情况,阻尼系数的减小一定程度上可以增大摩擦系数的取值范围并避免系统失稳,但总体来说,系统需要更多的碰撞次数来衰减扰动能量;而对于接触刚度较大的情况,阻尼系数减小压缩了摩擦系数的选择范围。
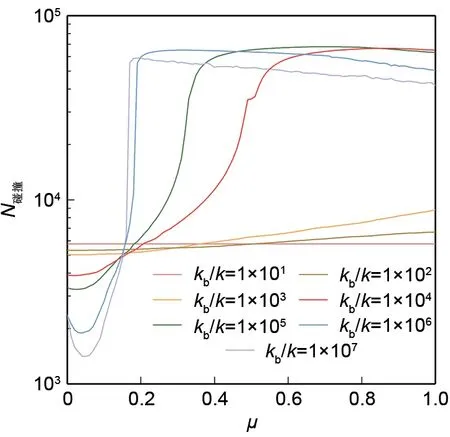
图10 不同kb下,N碰撞随μ的变化曲线(c1=0.1 c)Fig.10 N碰撞withμunder different kb(c1=0.1 c)

图11 μ最佳和μ临界随kb的变化Fig.11μ最佳andμ临界with different kb
4 结 论
针对正常运转的飞轮转子受到扰动后、转子轴颈可能与保护轴承内圈发生碰摩的现象,通过数值计算得到如下结论。
(1)转子受到扰动后,可以利用与定子之间的碰摩作用耗散扰动能量,使其回归稳定运行的状态并提升系统稳定性。
(2)设计与定子间的接触参数时,摩擦系数的选择需要考虑到接触刚度。在实际接触刚度范围内,能提升系统稳定性的摩擦系数的取值范围、随接触刚度的增大而变得狭窄。过大的摩擦系数可能带来负阻尼,使系统在碰摩过程中失稳。
(3)摩擦系数的选择还需要考虑到系统阻尼系数。
