问题链思维在一类初中动态几何问题上的体现

龚含笑 张侨平 唐恒钧

【摘 要】 动态几何问题是初中数学中对学生有挑战的一类问题.因为涉及多个数学概念以及蕴含图形的动态变化，这类问题在学生数学思维培养上具有重要价值，因此值得在教学中有意识地应用.问题链教学通过简化的子问题为学生提供思维台阶，以降低学生研究这类问题的门槛;另一方面又通过问题间所具有的思维关系，为学生提供思考这类问题的思维脉络，使学生有机会在解决问题中发展数学思维.

【关键词】 问题链;思维脉络;动态几何问题

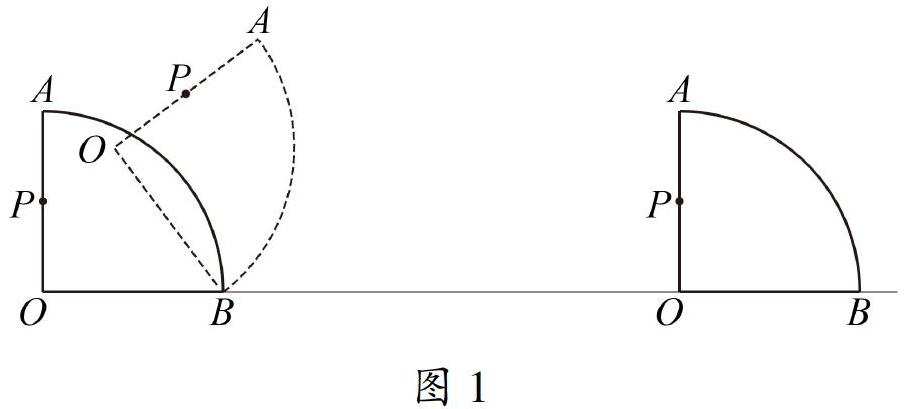
初中生学习几何，特别是平面几何，已经从小学阶段认识图形及其基本性质，转而开始探讨几何图形的结构特点、推论和证明一些几何结论.如果再融合几何图形的变化（如平移、旋转、对称等），相应的几何问题就更复杂了.动态几何问题即为这样一类问题，并频繁出现在中考试题中，相应的解题分析也不少[1-2].2020年中考结束后，以下问题（图1）曾引起热议.该题给出了图形初始位置和终结位置，研究动点P的运动路线即为研究符合条件的所有点的集合.如果只是直观观察和想象这一动态变化，学生在有限的答题时间内只用纸笔作答并不容易.事实上，通过四分之一圆周图形的翻滚，本题中点P的运动路径包含线段和圆弧，路线计算比较复杂，已经超出了初中的知识水平.

问题 如图1所示，将一个半径OA=10cm，圆心角∠AOB=90°的扇形纸板放置在水平面的一条射线OM上，在没有滑动的情况下，将扇形AOB沿射线OM翻滚至OB再次回到OM上时，则半径OA的中点P运动的路线长为_______________cm.（计算结果不取近似值）

如果撇开这一问题出现在试题中是否合理的讨论不说，将其作为一个教学问题进行探讨，则可以启发我们思考以下两个问题：一是设计这一类问题的教学目标为何？二是该如何有效地组织教学以启发学生的数学思维？本文试图立足问题链思维对这两个问题进行探讨.

1 问题链思维

前面提到，学生学习几何的过程也是其几何思维逐步发展的过程.按照范希儿（Van Hiele）的几何思维发展层次理论，这一过程包括视觉的（仅经视觉观察来辨认图形）、描述的（能分析并确认图形的性质、组成要素及其之间的关系）、非形式演绎的（探索图形的内在性质及各图形间的包含关系）、形式演绎的（能运用演绎逻辑进行推理证明）和严密的（能在不同的共设体系中建立定理）等五个层次.由此可见，无论是认识静态的几何图形还是动态图形的变化，均从视觉观察开始，及至初中，达到第三或者第四层次.上述动态几何问题，学生仅凭借几何直观很难想象出动态变化的过程，以及在此过程中图形的位置.因此，我们需要将这一变化过程由浅入深地进行分层次剖析，并借助代数的方法，逐步抽象和模型化[3].也可以说，解决这类几何问题有助于学生经历从直观几何、演绎几何到解析几何的学习历程.

为了促进学生思维过程与思维活动的有序整合与规划，我们借助问题链的思维对此进行分析.数学问题链重视数学问题之间的关联，以核心数学思维作为基本依据，为学习者的深度思考提供内在脉络.核心数学思维是指数学特有的或多个学科共有的、具有方法论意义的思维方式与方法，比如逻辑推理、一般化与特殊化、分析与综合、类比、化归等，体现了数学发展的基本方式[4].问题链思维是一种辩证的动态思维，以问题为抓手，以核心数学思维为主线，兼具建构性与逻辑性.设计问题链是开展数学教学活动的一种基本方法，它的目的则是希望通过设计以数学思维方法为主线的、不断演进和发展的主干问题序列，引导学习者逐步从点状的零散思维向整体系统化思维发展.因此，问题链在设计的过程中，往往不是由某一种数学核心思维指导而成，而是采用混合的形式以适应需要.

2 以问题链设计来理解动态几何问题

在初中阶段，平面图形的运动实际上是图形中的点的运动.“点的集合”主要集中在两个方面.一是从几何图形的直观性来看，作为平面几何中“线”的本质，所谓点动成线.比如，角平分线可以看成到角两边的距离相等的点的集合，线段垂直平分线可以看成到线段两端点的距离相等的点的集合，而圆即为到定点的距离等于定长的点的集合.另一方面，从几何图形的解析性来看，作为函数图像的本质.坐标赋予了每一个几何点解析意义，坐标满足一定函数关系的点的集合即为该函数的图像.比如，一次函数的图像为直线，反比例函数的图像为双曲线，二次函数的图像为抛物线.因此，求解点的运动路径主要有几何法、解析法两种方法，而点的运动路径主要分成直线型（直线、射线、线段）、曲线型（圆或圆弧、双曲线、抛物线）两类.

本文一开始提到的问题，涉及的图形尽管是一个扇形，但包含的路径有直线和曲线两种.图形的翻滚牵涉到直线图形和曲线图形上点的变化，想要直接求解，难度较大.我们可以借助问题链的设计思维，通过一些有关联的中间问题的过渡来分步解决.换言之，将问题分成几个中间问题，再对各问层层深入，利用中间问题的解决提供部分结果与解题方法.其中，各个中间问题之间既相对独立，又彼此之间存在联系.因此，在分析与综合思维方法的指导下，我们尝试构建以下问题综合链，从不同的角度来解决图形的翻滚问题，启发学生的数学思维.

2.1 简单图形的翻滚问题

要解答一个困难的问题，可以试图先从简单的问题出发.在初中阶段，简单平面图形主要有多边形（包括三角形）与扇形（包括圆），从它们入手进行归类分析，可以帮助我们探索此类运动变化中的规律.

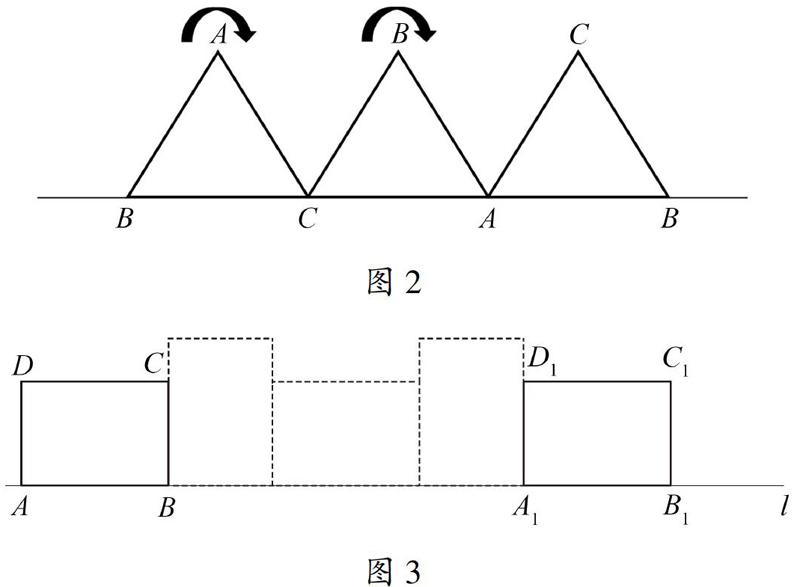
问题1.1 一块等边三角形的木板，边长为1，现将木板沿水平线从左向右翻滚（如图2），那么B点从开始至结束所走过的路径长度为______________.

问题1.2 矩形ABCD的边AB=8，AD=6，现将矩形ABCD放在直线l上且沿著l向右作无滑动地翻滚，当它翻滚至类似开始的位置A1B1C1D1时（如图3），则顶点A所经过的路线长是_____________.

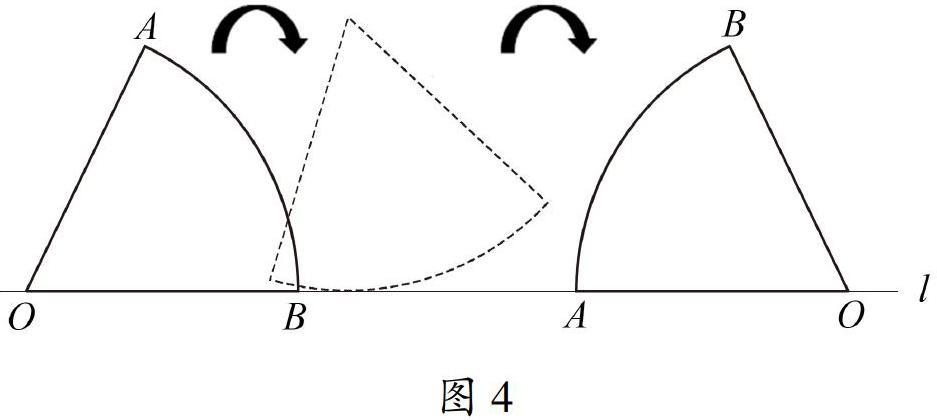
问题1.3 将半径1，圆心角为60°的扇形AOB，在直线l上向右作无滑动的翻滚至扇形A′O′B′处（如图4），则顶点O经过的路线长为_______________.

问题1.4 如图5，一个圆心角为270°，半径为2m的扇形工件，未搬动前如图所示，A，B两点触地放置，搬动时，先将扇形以B为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A，B两点再次触地时停止，则圆心O所经过的路线长是_______________m.

简单图形的翻滚问题为动态几何的基础问题，问题1.1至1.4的解决都只要找出所求点在运动过程中的旋转圆心、旋转时圆的半径以及圆心角，并利用扇形的弧长公式计算其路径长度即可.如果是圆弧在直线上滚动的话，圆心的路径是直线型.事实上，简单图形的翻滚问题是单动点路径问题，所形成的路径是直线型或曲线型（一般为圆或圆弧）.我们可以进一步思考，双动点路径问题，甚至是多动点路径问题该如何处理？因此，下面我们继续探讨不同路线类型的点的运动.

2.2 直线型运动路径

点的运动路径是直线型，一般有两种情况.一是动点到某直线的距离为定值.二是动点与起始时刻位置的点的连线与某条直线的夹角为定值.显然，第二种难度比第一种大，后者一般需要通过建立直角坐标系解决.

问题2.1 如图6，已知AB=10，P是线段AB上的动点，分别以AP，PB为边在线段AB的同侧作等边△ACP和△PDB，连接CD，设CD的中点为G，当点P从点A运动到点B时，则点G运动路径的长是___________________________.

问题2.2 如图7，在Rt△ABC中，∠C=90°，AC=10，BC=30，动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动，动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动，连接PQ，点P、Q分别从点B、C同时出发，当其中一点到达端点时，另一点也随之停止运动，在整个运动过程中，线段PQ的中点所经过的路程长为________________.

双动点直线型运动路径问题的解决从判断动点类型（主动点、从动点）开始，进而确定与主、从动点联系紧密的关键点.前面提到，求解点的运动路径主要有几何法、解析法两种方法.从几何方法入手，问题2.1既可以考虑补形（构造平行四边形CPDH），又可以考虑作垂线段（分别过点C、G、D作AB的垂线段）;而在问题2.2中，PQ中点在运动过程中到已知直线的距离并不为定值，考虑该动点与起始时刻位置的点的连线与某条直线的夹角为定值，因此通过作垂线段构造相似关系，进而得到与夹角相关的边长.从解析法入手，只要建立合适的直角坐标系，并表示相关点的坐标，当动点的横、纵坐标都可用同一个变量x（指数为1）表示时即可确定动点路径是直线型，最后求解线段的长度.

2.3 曲线型运动路径

在初中阶段，几何动点的曲线型运动路径一般为圆或圆弧.要解决此类问题，主要分为两种情况.一是动点到某点的距离为定值.其原理为圆的本质，即到定点的距离等于定长的点的集合为圆.二是动点和某两个定点所组成的夹角为固定值.其原理为圆周角定理的推论，相等的圆周角所对的弧也相等.

问题3.1 如图8，一根长为2米的木棒AB斜靠在墙角处，此时BC为1米，当A点下滑至A′处并且A′C=1米时，木棒AB的中点P运动的路径长为__________________米.

问题3.2 如图9，在Rt△ABC中，∠C=90°，AC=BC=4，点P在AC上运动，将纸片沿PB折叠，得到点C的对应点D（P在C点时，点C的对应点是本身），则折叠过程中对应点D的路径长是____________________.

问题3.3 如图10，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为__________________cm.

问题3.4 如图11，△ABC，△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M.当△EFG绕点D旋转时，线段BM长的最小值为____________________.

第一种情况的问题较为基础.比如，问题3.1利用直角三角形中斜边上的中线等于斜边的一半，且直角顶点固定、斜边长度固定，因此确定点P的路径是圆弧型;问题3.2则利用对称变换得到BD=BC，确定点D的路径为以点B为圆心、线段BD为半径的圆弧.第二种情况的突破口在于结合已有条件找到与所求动点相关的定角.比如，问题3.3利用内心的定义构造全等三角形，确定∠AIO为定角，进而明确点I的运动路径并计算其长度;问题3.4则利用等边三角形“三线合一”的性质构造相似三角形，确定∠AMC为直角，进而明确点M的运动轨迹并计算BM长的最小值.

3 若干反思

數学是思维的体操，数学思维中的矛盾一般表现出“问题性”，而问题是思维的聚焦点，可见问题与思维存在着直接联系.数学问题的解决需要教师对学生的探究进行恰当的引导，构建问题链是提升学生数学思维的一种重要方法.面对一个数学问题，通过对它进行分析、综合、引申、深化、收敛、推广得到新的问题，然后确定问题间的联系，最终能形成问题链.在问题链的学习过程中，问题的逐次推进是在核心数学思维指导下进行的.有形的问题链是一系列彼此关联又独立的问题，无形的问题链则是学生头脑中关联起来的数学思维.

事实上，数学知识的内部结构是一个纵横交错的命题链结构，也可用类似于问题链的结构来描述和解释[5].问题链的构建具有多向性或分枝性，不同主干问题具有交叉联系，其中所涉及的知识是纵横交错的，所涉及的方法是多样且相通的，因此实际教学时强调知识的多维度展开与方法的多样性[6-7].这其实也反映了数学思维的复杂性.比如，问题2与3的解决过程中都涉及几何的多个知识，可以用几何方法解决.与此同时，直线型路径问题也可通过建立直角坐标系利用解析法进行解决，几何与代数是相通互换的.唯一存在困难的是，圆或圆弧型路径的解析式在初中阶段尚未涉及，只能通过几何方法进行解决.

问题链作为组织教学的主要逻辑，在实施时应考虑以问题功能为依据为学生提供思考与表达的空间.这即是指，问题并不是完全由教师呈现在课堂上，有些问题更希望学生能在思维脉络引领下自主发现和提出[4].比如，文中的问题（中考题）是起点性问题，触发学习的产生，由教师提出.但之后的问题1及其子问题并不完全由教师一一呈现，而是学生的结合自己的学情自发提出从三角形到长方形，再到扇形，甚至菱形、平行四边形等图形的翻滚问题.最后，由教师提出提炼性问题，引导学生归纳简单图形翻滚问题的不变本质，形成这类问题的通性通法，并根据路径的不同类型增加动点引申出问题2与3.这样一来，学生通过有脉络的思考过程形成自己的理解与体悟，又通过互动交流促进思考过程的重新梳理与语言外化，更大程度地发挥自由性、主动性、积极性、创造性，这正是促进数学思维发展的最佳状态.

参考文献

[1]徐骏.盘点图形在直线上翻滚过程中和点相关的一类路径（位置）问题[J].中学数学杂志，2011（04）：57-59.

[2]马恒平.例谈动点路径长问题[J].中学数学杂志，2012（10）：42-44.

[3]Van Hiele P M. Structure and Insight： A Theory of Mathematics Education[M]. Orlando， FL： Academic Press. 1986.

[4]唐恒钧，张维忠，陈碧芬.基于深度理解的问题链教学[J].教育发展研究，2020，40（04）：53-57.

[5]黄光荣.问题链方法与数学思维[J].数学教育学报，2003（02）：35-37.

[6]龚含笑，唐恒钧.基于挑战性任务的数学问题链教学研究——基于“余弦定理”的教学探索[J].中学数学，2020（09）：13-15.

[7]龚含笑，唐恒钧.数学方法论指导下的数学问题链教学研究——基于“空间两点间的距离公式”教学探索[J].中学数学教学参考，2018（34）：19-21.作者简介 龚含笑（1995—），女，浙江慈溪人，教育硕士，宁波外国语学校数学教师，主要从事数学课程与教学研究.