圆柱形蓄冰桶内融冰换热参数优化设计

黄凯良,崔蓝予

(沈阳建筑大学市政与环境工程学院,辽宁 沈阳 110168)

冰蓄冷空调技术作为减缓电网负荷的有效措施,近年来得到了重大发展。冰蓄冷空调技术指的是利用夜间的低谷电使电动制冷机制冷,通过蓄冷介质的潜热和显热特性将冷量储存起来,在白天用电高峰期将储存的冷量释放出来,用于满足房间所需冷负荷,实现削峰填谷。该技术在提高电网负荷率的同时,也降低了空调的运行费用,使经济效益得到提高。目前我国的冰蓄冷空调技术还处于发展阶段,有着很好的发展前景和应用潜力。

冰蓄冷按制冰方式可分为静态制冰和动态制冰,盘管式蓄冰是静态制冰系统的一种应用形式。融冰释冷过程中,根据其融冰方式的不同,又可分为内融冰和外融冰两种形式,内融冰系统与外融冰相比具有可以完全冻结,蓄冰率高,占地面积小,以及无需控制冰层厚度,不用增加搅拌设备等优点[1-2]。具体的融冰过程涉及复杂的相变,因此必须对其进行深入的相变传热分析。ZHENG Zonghe等[3]对内融冰盘管蓄冰系统进行了模拟,建立了相应的数学模型,重点分析了管材、管径和热阻对整个结冰和融冰过程的影响。YANG Tianrun等[4]通过在Ansys中建立三维的CFD模型,研究了制冷剂不同入口温度下盘管蓄冷板的蓄冰过程。LPEZ-NAVARRO A等[5]研究了逆流螺旋盘管蓄冰罐的冻结过程,对冷水机组性能,结冰过程以及装置能耗进行了分析。ZHU Yingxin等[6]建立了针对于水平管蓄冰罐开发的偏心圆筒模型,研究了冰水密度差对融冰过程产生的影响。K.CHO等[7]研究了球形容器中石蜡在冻结和熔融过程中的热特性,相比于冻结过程,熔融过程中的入口温度、初始温度和雷诺数对平均传热系数的影响更大。在冷冻和熔融过程中,石蜡的平均传热系数比水的平均传热系数大40%。同时,在经济性方面,S.SEPEHR 等[8]对冰蓄能系统(ITES)系统的热经济性进行了优化,考虑资本成本,运行成本以及环境污染惩罚成本,得出ITES系统的平均用电量和二氧化碳排放量分别低于常规空调系统的9%和9.8%。H.E.ABDELRAHMAN等[9]对双同心螺旋盘管蓄冰系统的热性能进行了实验分析,结果表明大约90%的能量储存在59%～74%完全充电时间内。笔者针对盘管式内融冰蓄冰桶的融冰特性进行研究,采用单一变量原则,在保证其他参数保持不变的情况下,通过数值模拟对载冷剂的出口温度,水层半径以及释冷量进行讨论,分析以上参数对盘管式内融冰动态性能产生的影响。为内融冰式圆柱形蓄冰桶的换热参数优化提供依据。

1 蓄冰桶数学模型

在供冷过程中,冰的融化分为两个阶段,分别为冰未完全融化时的潜热释冷阶段和完全融化以后的显热释冷阶段。实际的换热过程会受到很多因素的影响,较为复杂,为简化模型计算,针对模型做出假设:①冷媒即载冷剂入口温度恒定;②忽略管道的轴向传热,认为传热仅发生在径向[10];③取冷过程中,忽略冰桶与环境热交换;④取冷过程中相变界面呈同心圆管状变化,冰块固定无上浮偏斜情况,整个过程是对称的;⑤忽略由冰水相变引起的体积变化[11];⑥潜热释冷阶段下桶内为冰水混合物,水温默认0 ℃。

1.1 蓄冰桶热平衡方程

蓄冰桶由内外结构组成,内装置直径为 0.6 m,高度为0.6 m,壁厚为1 mm;外装置直径为0.8 m,高度为0.6 m,壁厚为1 mm,外装置在侧面开0.10 m×0.10 m的进风口与出风口,外装置粘贴保温材料,保温材料外带有防止太阳辐射的材料,保温材料厚度0.11 m,蓄冰桶装置图如图1所示。在沈阳地区环境条件下,按照沈阳地区最热月室外气象参数,该装置制冰阶段可以达到的蓄冰半径为120 cm[12]。

图1 蓄冰桶装置图

笔者在蓄冰桶内部设有由内到外共3组换热盘管,每组10层,材料为铝塑复合焊接管,其导热系数为0.45 W/(m·K)。3组盘管对应半径分别为:r1=115 mm,r2=165 mm,r3=215 mm,盘管总长度为34.2 m。

融冰开始时,载冷剂进入换热盘管流经蓄冰桶内部,将能量通过盘管传递给冰层,使其由内到外开始融化。与此同时,载冷剂以比较低的温度流出,带走冰桶蓄存的冷量。

根据能量守恒定律,载冷剂在蓄冰盘管内获得的冷量等于冰层融化释放的冷量。

q=G·ρref·Cref(Ti-To)=Kl·L·ΔTm.

(1)

(2)

式中:q为单位时间换热量,kW;Kl为单位长度盘管传热系数,kW/(m·K);L为盘管长度,m;G为体积流量,m3/s;Cref为载冷剂比热,kJ/(kg·℃);ρref为载冷剂密度,kg/m3;Ti、To为载冷剂进出口温度,℃;Tn为融冰过程中盘管外圆环内的水温,近似于水的冰点,即Tw =0 ℃;ΔTm为对数平均温差。

1.2 蓄冰桶盘管传热方程

根据热阻网络法,求解单位长度总热阻R.

(3)

(4)

(5)

式中:αref为载冷剂对流换热系数,W/(m2·K);λtub为换热盘管导热系数,W/(m2·K);di为盘管内直径,m;do为盘管外直径,m。

1.2.1 载冷剂换热系数

采用的载冷剂为体积分数25%的乙二醇水溶液,乙二醇溶液具有热容较大,传热性能好,化学性能稳定等优点[11]。

换热管内载冷剂的换热系数αref与雷诺数Re有关:

①当Re>2 300时,制冷剂在盘管中处于紊流工况,按迪图斯—贝尔特[14]公式计算:

Nu=0.023Re0.8Pr0.4.

(6)

②当Re≤2 300且Re·Pr·di/L<10时,载冷剂在管内流动处于热充分发展区。定性温度为载冷剂进出口平均温度;定型尺寸为盘管内径。

(7)

(8)

式中:Nu为努谢尔特准则数;Pr为普朗特准则数。

1.2.2 融水环热阻及总换热量

融冰释冷时盘管与冰之间形成的同心水环,不仅存在导热热阻,还存在对流换热热阻,其具体的换热计算过程较为复杂。为简化计算,特引入当量导热热阻的概念,使用留斯勃提出的有效导热系数λeff进行计算,查找相关资料得到同心长圆柱内自然对流对导热影响的经验公式[15]为

(9)

(10)

因此可以求得:

(11)

式中:λw为水导热系数,W/(m2·K);λeff为有效导热系数,W/(m2·K);Ra为瑞利数;dw为水层直径,m。

1.3 载冷剂出口温度及水层半径

随着取冷的不断进行,冰层厚度一直处于变化之中。根据蓄冰桶的能量平衡方程,将融冰过程分为n个时间段,每个时间段内载冷剂带走的冷量总和等于冰层融化发生相变释放的冷量。

(12)

生成水环直径迭代关系式:

(13)

载冷剂出口温度关系式:

To=Ti·e-kl·L/G·ρref·Cref.

(14)

如果把蓄冰桶实际换热量与最大可能换热量之比定义为蓄冰桶效能ε。

(15)

实际放冷量为

Qs=ε·G·ρref·Cref(Ti-Tf)=

ε·G·ρref·Cref·Ti.

(16)

式中:Qs为冰层实际放冷量,kW;hice为冰的熔解热,334 kJ/kg;Tf为水的冰点,Tf=0 ℃。

1.4 模型求解

MATLAB软件具有强大的数值分析、矩阵运算、图形图像处理、信号处理和仿真功能。笔者通过将数学模型编写为程序以用于MATLAB求解,由于方程各参数之间相互耦合,故采用迭代法。在用MATLAB模拟分析时,选取时间步长Δτ=300 s,设换热盘管外径为20 mm,内径为16 mm,盘管总长34.2 m。乙二醇水溶液物理性质参数如表1所示,同时认为蓄冷介质0 ℃以上时为水,0 ℃及0 ℃以下为冰,其物性参数如表1、表2所示。

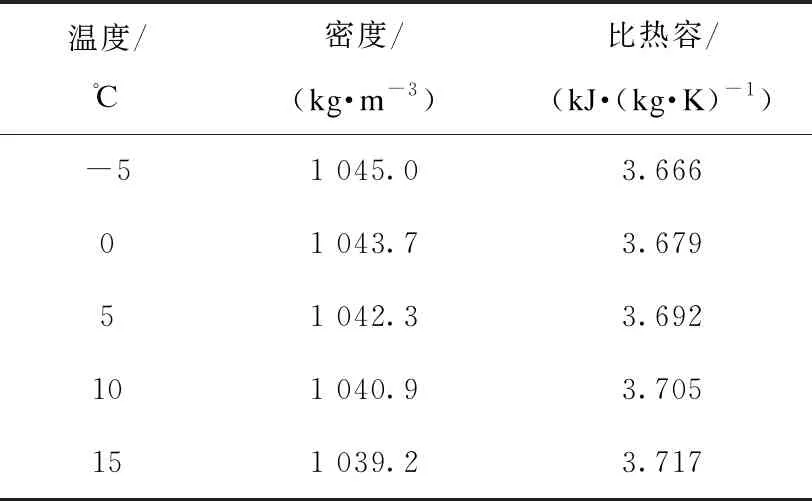
表1 乙二醇水溶液物理性质参数

表2 水的热物理性质参数表

为对照验证MATLAB求解的准确性,运用COMSOL Multiphysics分析冰桶传热特性。二者均可以对蓄冰桶融冰过程中换热管的热交换特性以及管外的融冰释冷动态特性进行分析,从而相互对照证明MATLAB求解的可靠性。在使用COMSOL模拟的过程中,为简化模型,将盘管整体视为长直圆柱形管路进行求解。图2为MATLAB求解流程图。

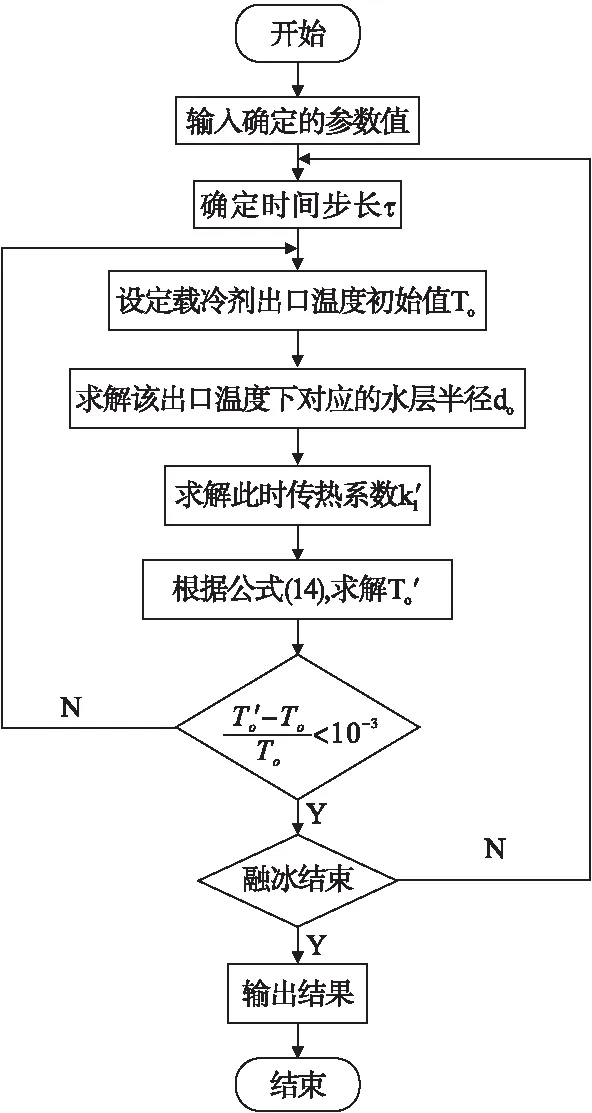
图2 迭代流程图

2 结果与分析

2.1 两种求解方式的比较

为了验证笔者通过MATLAB模拟的内融冰换热热性能的准确性,使用COMSOL Multiphysic(COMSOL Multiphysic 5.4)进行换热流体传热的模拟分析。COMSOL Multiphysic是一款可以描述和模拟各种物理现象的软件,具有强大的计算能力和耦合分析能力,可以通过其建立各种物理现象的数学模型并进行模拟计算[16-21]。笔者通过构建冰桶三维立体模型,采用与MATLAB相同模拟参数,图3为COMSOL蓄冰桶模拟图。

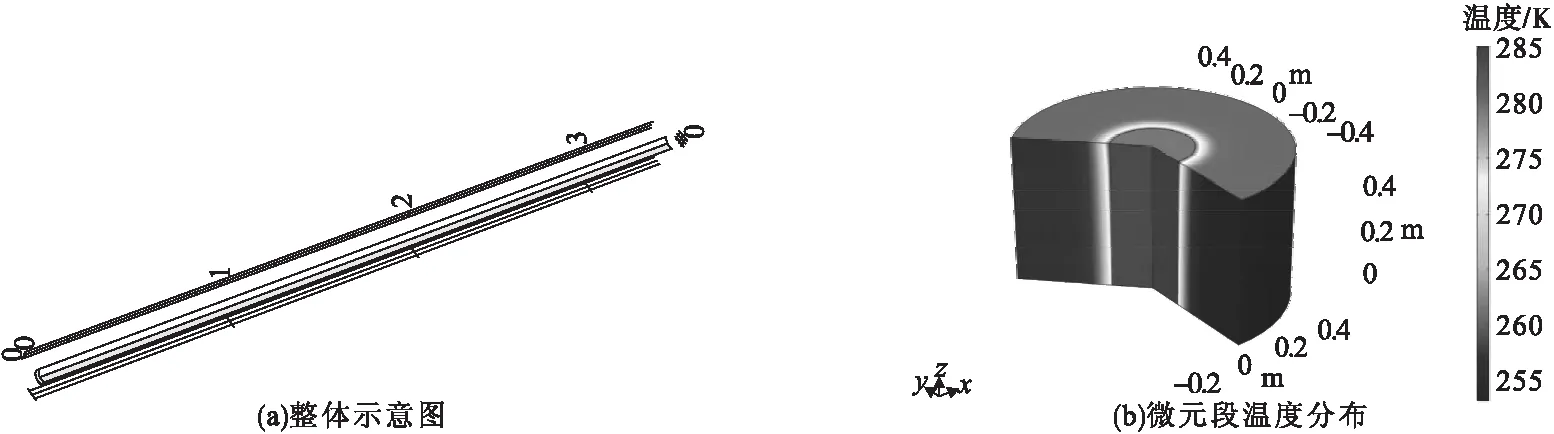
图3 COMSOL蓄冰桶模拟图

模拟过程中,采用载冷剂进口温度为10 ℃,流量0.3 L/s,分析出口温度和水层半径的变化情况,并与MATLAB模拟结果参照对比(见图4)。两者的模拟结果趋势基本一致,出口温度最大相对误差为3.37%,融冰半径最大相对误差为2.84%。

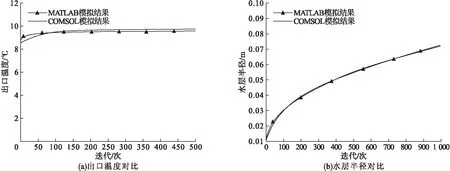
图4 COMSOL、MATLAB模拟结果对比

2.2 载冷剂进口温度对融冰产生的影响

为了研究载冷剂入口温度对融冰过程产生的影响,设载冷剂流量为0.2 L/s,载冷剂入口温度分别为8 ℃、10 ℃和12 ℃。图5为不同入口温度下3种融冰特性变化情况。

从图5(a)可以看出,载冷剂入口温度越高,相同时间内形成的水环半径越大。随着融冰的进行,水层半径增长速度逐渐减小,这是因为冰层融化后水层厚度增加导致传热热阻增加,换热速度减缓。图5(b)可以看出,较高的入口温度对应较高的出口温度。当载冷剂入口温度分别为8 ℃、10 ℃和12 ℃时,对应的出口温度分别保持在7.4 ℃、9.3 ℃和11.2 ℃。同时,载冷剂的出口温度随着融冰的进行而增长,出口温度逐渐趋于进口温度。这是因为水层厚度增加导致传热系数减小,换热量的减小,从而导致进出口温差减小。图5(c)表示入口温度越高,在相同融冰时间内释冷量越大。释冷量随着冰层的融化逐渐减小,这是由于换热热阻加大导致的。

图5 不同入口温度下3种融冰特性变化

2.3 载冷剂流量对融冰产生的影响

为了探究载冷剂流量对融冰特性产生的影响,设载冷剂进口温度恒定为10 ℃,流量分别为0.2 L/s、0.3 L/s和0.4 L/s。分析载冷剂入口流量对出口温度大小、水层半径和释冷量增长速率的影响。载冷剂流量加大会导致较高的出口温度和较大的释冷速率。这是因为较大的流量对应较高的流速,雷诺数Re和努谢尔特数Nu增大,所以传热速率随着流量的增大而加大。图6为不同流量下3种融冰特性变化情况。从图6(a)可以看出。当流量为0.2 L/s、0.3 L/s和0.4 L/s时,水环半径的增长速率均是初始增长速度较快,随后减缓,改变流量对融冰半径的影响不大。从图6(b)可以看出,流量分别是0.2 L/s、0.3 L/s和0.4 L/s时,载冷剂的出口温度最终保持在9.3 ℃、9.6 ℃和9.7 ℃。从图6(c)可以看出,在0.2 L/s、0.3 L/s和0.4 L/s的进口流量下,释冷量的变化趋势基本相同,流量的改变对释冷量的影响微乎其微。

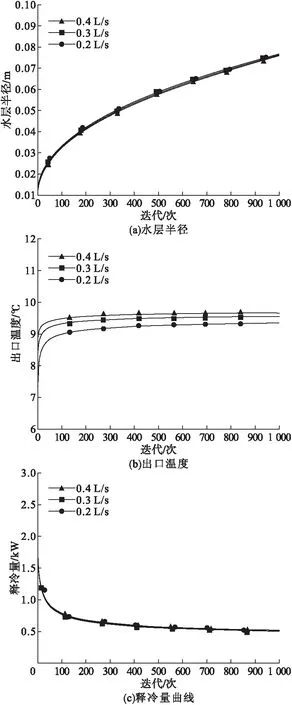
图6 不同流量下3种融冰特性变化

2.4 盘管外径与蓄冰桶外径之间比例对融冰产生的影响

假设蓄冰桶外径为0.6 m,改变盘管直径大小,分析两者之间比例参数对融冰产生的影响。分别设置盘管外径为24 mm、20 mm、16 mm、12 mm,两者之间比例分别为0.04、0.033、0.027、0.02。分析进口温度10 ℃,流量为0.3 L/s时,4种不同比例出口温度和融冰半径随时间的变化情况如图7所示。从图7(a)可以看出,4条曲线由上至下对应的盘管外径分别为12 mm、16 mm、20 mm和24 mm,比例分别对应为0.02、0.027、0.033和0.04。在换冷刚开始时,盘管外径相对于冰桶外径的比例越大,对应的载冷剂出口温度越低,进出口温差越大。但随着融冰进行,可以明显看出,不同外径比例下的载冷剂出口温度很快趋于一致。从图7(b)可以看出,与图7(a)相反,4条曲线由上至下对应的比例分别为0.04、0.033、0.027和0.02。以外径为24 mm的盘管为参照,即对应比例为0.04,则其他3种外径比例下的冰桶整体融冰时间分别延长45%,81%和136%。可见,盘管外径相对于冰桶外径的比例越小,相同时间内产生的水环半径越小,整体的融冰时间越长。

图7 不同外径比例下出口温度与水层半径变化

3 结 论

(1)采用MATLAB和COMSOL两种求解手段对载冷剂出口温度和融冰半径进行求解。出口温度相对误差为3.37%,融冰半径相对误差为2.84%,误差偏小可以证明MATLAB求解结果的准确性与可靠性。

(2)流量一定时,载冷剂的入口温度越高,对应的出口温度越高。冷释放速率越高,相同时间内融冰半径越大,释冷量越大。因此在一定范围内提高载冷剂入口温度可以增加换热效果。

(3)进口温度一定,载冷剂的流量越大,对应的出口温度越高,释冷速率越大,完全释冷的时间越短。载冷剂进口流量与入口温度相比,改变流量对水层半径的增长和释冷量影响不大。

(4)改变盘管与蓄冰桶之间的外径比例,融冰初始阶段下两者之间比例越大,对应的出口温度越低,载冷剂进出口温差越大,但随着融冰进行,不同比例下的出口温度逐渐趋于相同。与之相反,两者之间比例越小对应的水层半径越小,完全融冰时间越长。所以,如果不考虑初始阶段的出口温度,在流速允许的范围内,盘管与蓄冰桶之间的外径比例越小越有利于延长融冰时间,最大限度利用冰桶蓄冷量。