GOST 的差分故障攻击*

谢 敏, 李嘉琪, 田 峰

1. 西安电子科技大学综合业务网理论及关键技术国家重点实验室, 西安710071

2. 陕西省区块链与安全计算重点实验室, 西安710071

1 引言

GOST 是前苏联时期的标准分组密码,最开始用于军事级别保密、政府通讯和苏联最大两家银行的保密工作, 直到1994 才正式公布, 目前依然是俄罗斯联邦的加密标准. 早期对GOST 的分析没有取得特别好的成果,学者们普遍认为GOST 对差分、线性等传统分析方法有足够好的安全性. 2010 年, GOST 被提交至国际标准化组织成为全球工业加密标准, 对GOST 的相关研究再次活跃起来. 2011 年, Courtois 等人[1]首次提出了对32 轮GOST 的差分分析方法, 所需时间复杂度约为2226; 同年Isobe[2]结合反射攻击和中间相遇攻击对GOST 算法进行了分析, 数据复杂度和时间复杂度为232和2225; 2012 年, Dinur 和Shamir 等人[3]对Isobe 的攻击做了改进, 所需数据复杂度和时间复杂度为232和2224; 2013 年, Kim[4]受Isobe 中间相遇攻击的启发, 找到了GOST 算法中2128组弱密钥, 针对这些密钥的攻击时间复杂度可以降为2125.5, 此外, 他还首次提出了GOST 上的差分故障攻击方法, 选择在算法第31 轮右侧引入半字节随机故障, 平均64 次故障注入可恢复GOST 算法的主密钥. 2019 年, Lu[5]针对GOST 算法提出了一种新的线性攻击方法, 所用区分器攻击32 轮GOST 需要的数据复杂度和时间复杂度均为2173.8.

Poschmann 等人[6]在2010 年研究了GOST 算法的物理实现, 指出GOST 算法完全符合轻量级密码算法的设计准则, 非常适用于低能耗的RFID 标签, 而该类设备的安全性极易受到旁路攻击的威胁, 差分故障攻击[7]作为旁路攻击中使用最为广泛的攻击手段之一, 对主流轻量级算法Lblock 和GIFT 等均有出色的攻击效果[8,9], 所以在GOST 算法应用于轻量级设备前进行差分故障分析是十分必要的.

2 GOST 分组密码介绍

2.1 GOST 加密算法

GOST 算法的分组长度为64 比特, 密钥长度为256 比特, 明文经过32 轮迭代得到密文. 该算法采用了广义Feistel 结构, 其轮函数如下式:

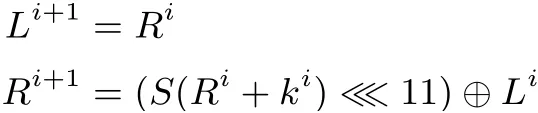
为方便描述, 我们将8 个S 盒分别记为S7,S6,··· ,S0, 如图1 所示.

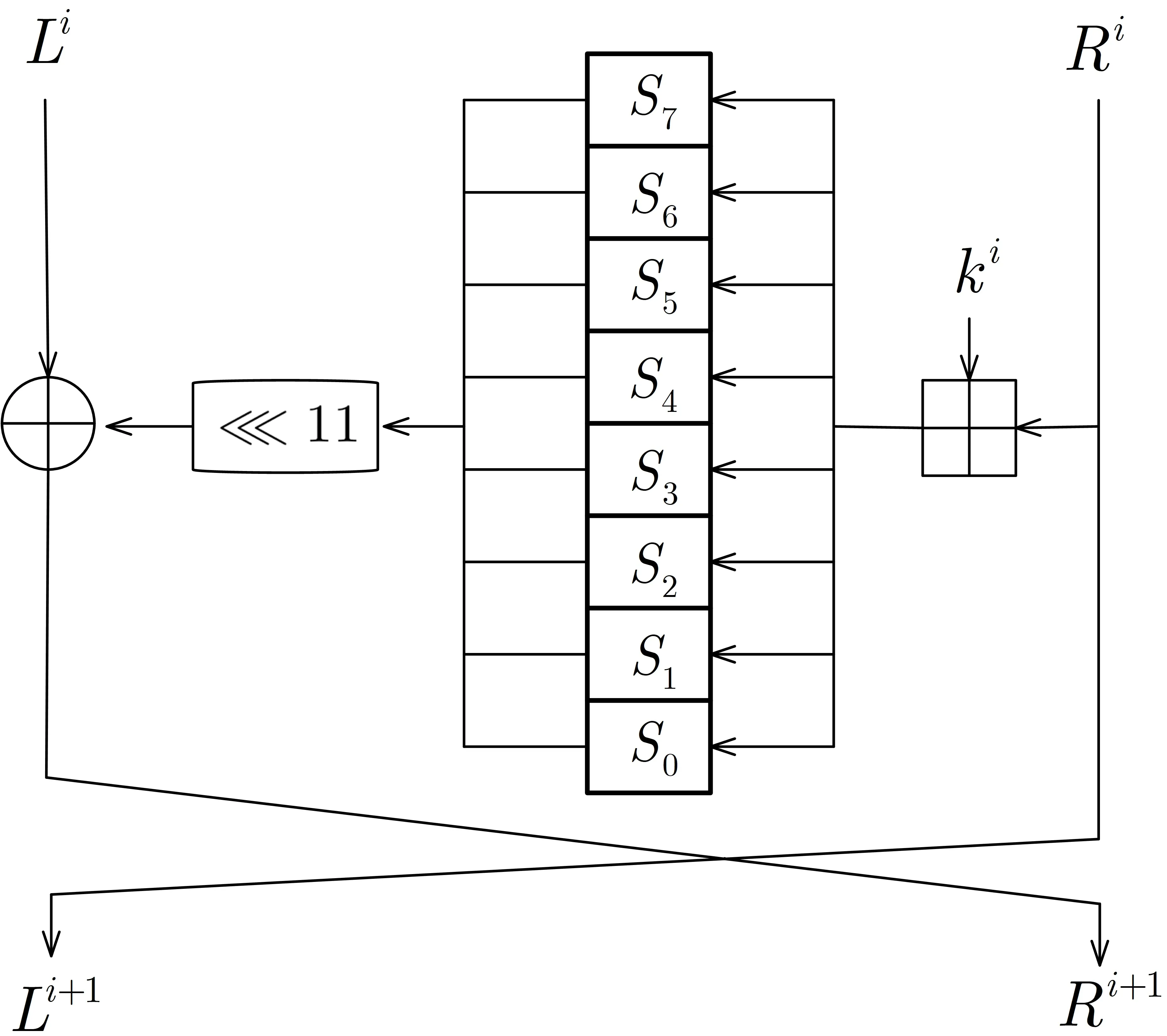
图1 GOST 单轮结构Figure 1 One round structure of GOST

对于GOST 算法, 其S 盒并不固定, 在不同的应用场景下会采用不同的S 盒, 常用于研究的S 盒为已公布的应用在俄联邦中央银行的S 盒, 如表1 所示.

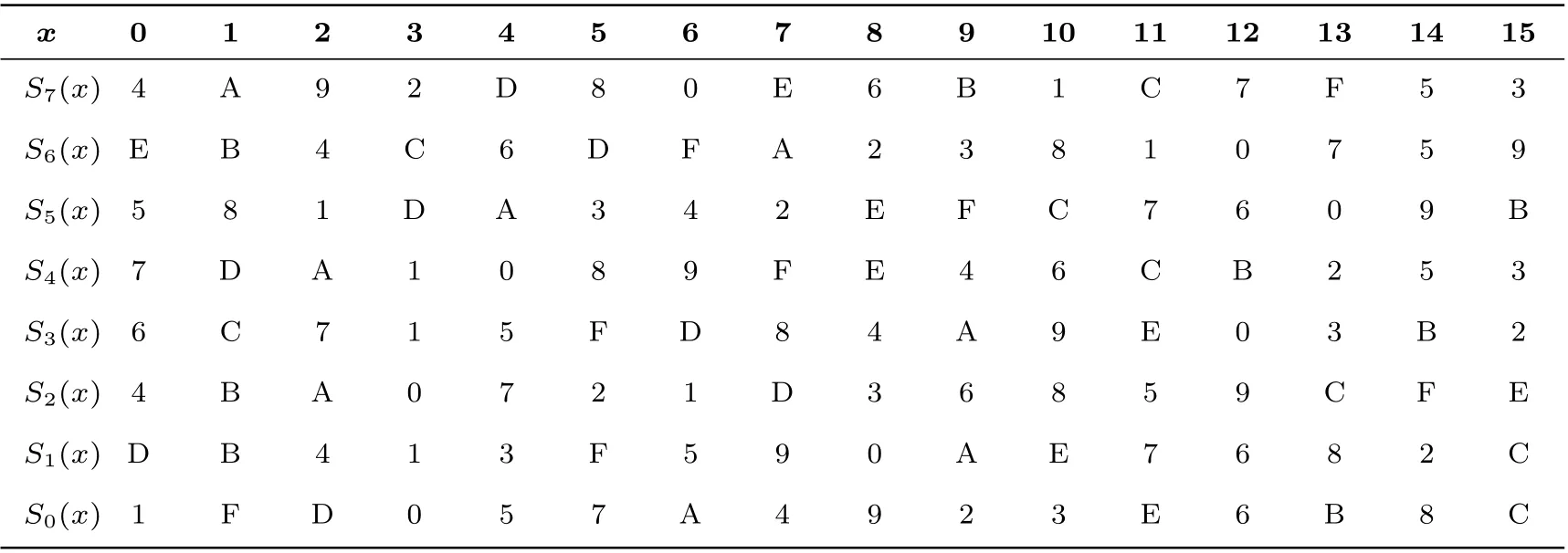
表1 GOST 的S 盒Table 1 S-box of GOST

2.2 GOST 的密钥扩展算法

GOST 算法的密钥扩展较为简单, 256 比特主密钥直接切分为8 个32 比特的子密钥, 分别记为K1,K2,··· ,K8, 前24 轮加密的轮密钥ki将按顺序循环使用这8 个子密钥, 最后8 轮则倒序使用.

3 GOST 的差分故障攻击

3.1 故障模型

本文用到的符号说明如下:

本文采用的故障模型包括以下两个基本假设:

(1) 攻击者拥有加密机的访问权限, 可以获得一定数量的明密文对(选择明文攻击, CPA).

(2) 攻击者可以在加密过程中的某一轮导入单字节随机故障以获取错误密文, 但是故障导入的具体位置和故障值是未知的.

3.2 攻击原理

对于第i轮右半段的输入Ri和S 盒的输入ini有ini=Ri+ki, 根据算法结构, 若Li+1已知, 则Ri可知, 此时一旦确定了S 盒的输入, 也就确定了轮密钥ki. 根据S 盒的差分分布特性, 可利用S 盒的输入输出差分对来获得其输入的信息.

为获得S 盒的输入差分, 对模加运算做如下等价转换: 对于加密过程的某一轮, 如第i轮, S 盒的32

为了获得S 盒的可能输入值, 我们研究了GOST 算法8 个S 盒的差分特性, 得到了每个S 盒在固定输入差分的情况下其输出差分与输入的对应关系, 这里仅列出S0的情况为例, 详见表2. 借助该对应关系,我们就可以从S 盒已知的输入输出差分获得其可能输入, 再通过故障的引入不断缩小其可能输入的范围,直到确定出S 盒输入的唯一值, 进而由关系ini=Ri+ki解出轮密钥, 最终利用密钥扩展算法, 将最后8轮轮密钥组合得到主密钥.

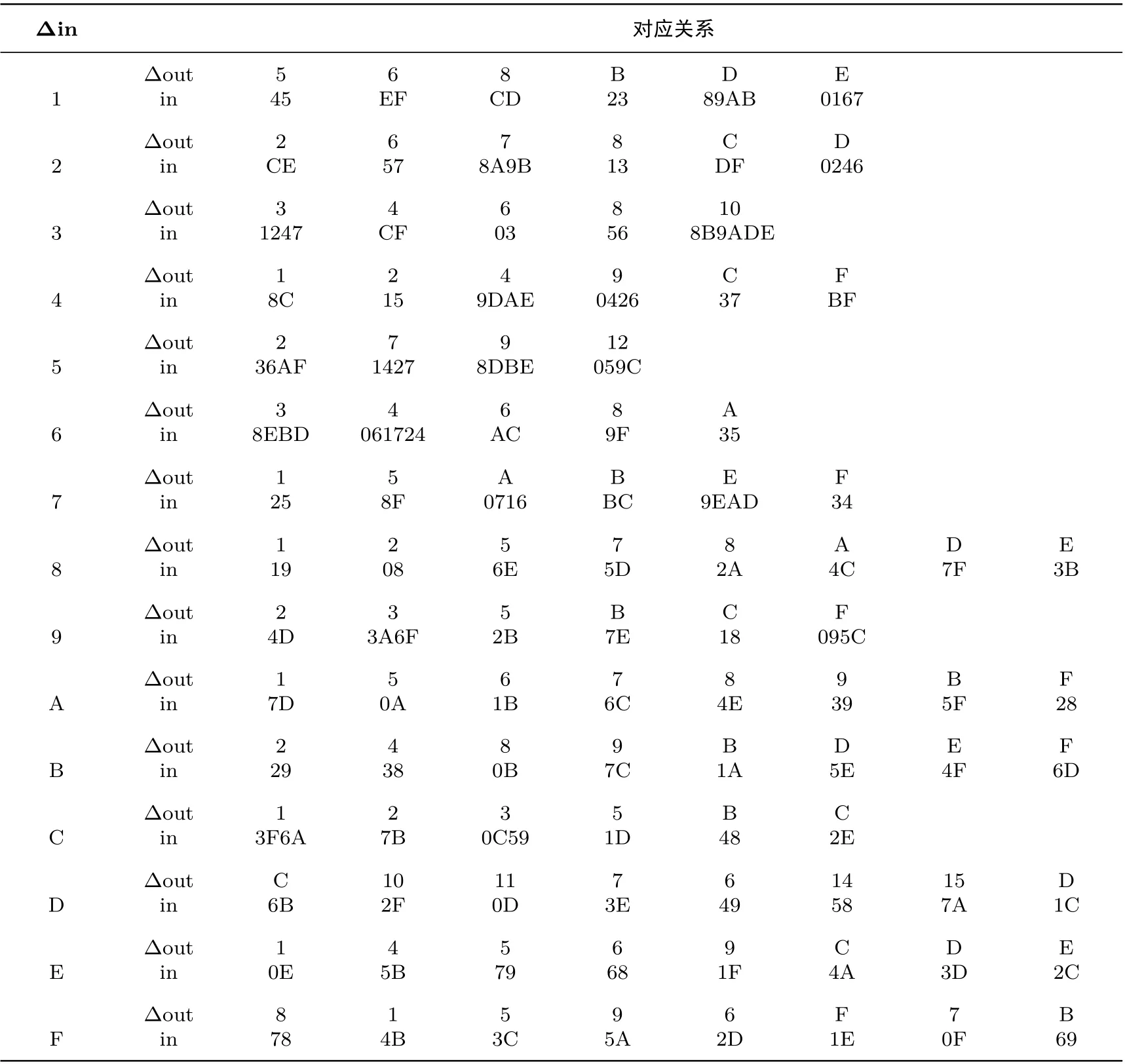
表2 S0 固定输入差分下输出差分与输入的对应关系Table 2 Corresponding relationship between output difference and input under fixed input difference of S0

3.3 GOST 差分故障攻击过程

3.3.1 模加运算转化后的差分扩散特性分析

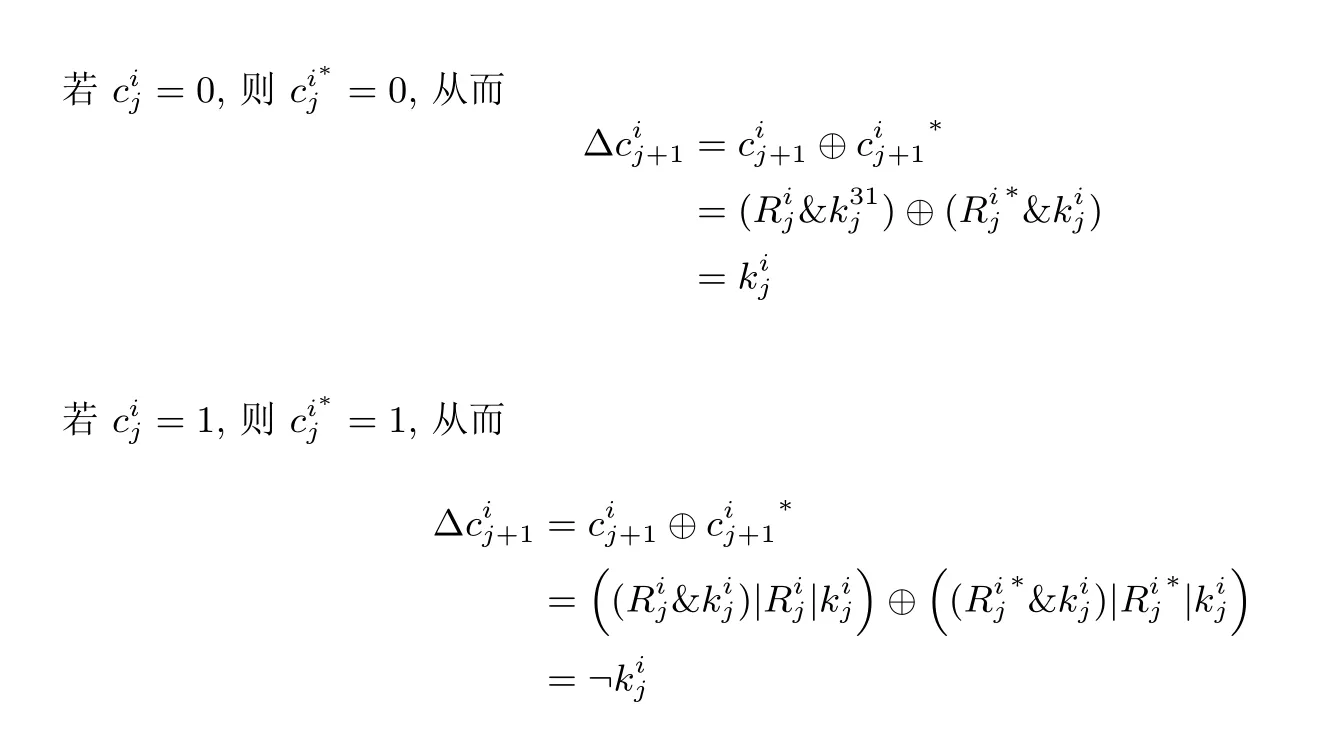
表3 ∆ = 1 时∆ 与, 关系表Table 3 Relationship among ∆, and when ∆ = 1

表3 ∆ = 1 时∆ 与, 关系表Table 3 Relationship among ∆, and when ∆ = 1

Ri j kij Rij|kij ∆ci j+1 0 0 0 0 0 1 1 0 1 1 1 1 1 1 1 0

3.3.2 基于半字节故障的分析

由3.2 节的攻击原理, 研究获取故障所在半字节对应S 盒的输入输出差分是攻击实现的关键, 在任何故障模型下, 都要做基于半字节故障的分析来获取S 盒的输入差分, 为此我们给出基于半字节故障的一般化分析如下:

表4 映射fTable 4 Mapping f

3.3.3 GOST 算法多轮扩散分析

3.3.2 节是基于半字节故障的一般化分析, 建立了活跃S 盒与密钥恢复之间的联系, 在已有分析的基础上, 活跃S 盒的数量将直接影响单次故障引入的恢复效率. 为此我们将故障时刻提前, 并采用扩散速度较快、引入难度较低的单字节随机故障, 利用GOST 的扩散层以及差分扩散特性实现快速的故障扩散, 经过4 轮可将单字节故障扩散到GOST 右侧输入的全部8 个半字节. 与之相比, Kim[4]对GOST 的差分故障攻击中采用了列举所有可能扩散路径的分析方法, 其故障模型很难从两轮扩展到多轮, 从而导致最终扩散产生的活跃S 盒数量较少, 大大限制了攻击的整体效果.

图2 给出了GOST 多轮差分扩散的示意图. 如图所示, 若在GOST 加密的第i轮右侧输入Ri处引入随机单字节故障, 经过左循环移11 位后, 将影响Ri+1的3 个半字节; 同理, 由于Ri+1和Li+1均有非零差分, 它们将影响Ri+2的5 个半字节, 从而再经过一轮的迭代,Ri处引入的随机单字节故障将影响Ri+3的全部8 个半字节.

图2 GOST 多轮差分扩散示意图Figure 2 Multi-round differential diffusion of GOST

3.3.4 GOST 算法完整攻击方案

1) 故障模型

由3.3.3 节的分析, 我们选择在第0 轮至第21 轮之间任意一轮右侧输入处引入单字节随机故障的模型, 引入难度较小, 且能够确保故障扩散后的影响覆盖最后8 轮右侧输入的全部64 个半字节, 该8 轮轮密钥组合即为GOST 算法256 比特主密钥.

2) 攻击步骤

由1) 的分析, 在第T(0≤T ≤21) 轮引入的单字节随机故障经过多轮扩散, 其影响将覆盖第24 到31 轮右侧输入的所有半字节, 这样对其中每个S 盒都能得到一组长为4 比特的输入输出差分对, 共计64组. 在第T轮右侧输入引入单字节随机故障M次, 可获得M组密文, 并由此计算出M组ΔR31和Δout31对, 密钥恢复步骤可总结为:

步骤1 恢复k31的第0 个半字节

步骤2 恢复k31的其他半字节

步骤3 恢复k30,k29,k28,k27,k26,k25,k24共7 轮的轮密钥

利用恢复后的k31向上解密一轮, 得到M组ΔR30和Δout30对, 然后用同样的方式恢复k30. 设恢复k30所需故障次数为N30.

同理, 我们可依次恢复其他6 轮的轮密钥k29,k28,k27,k26,k25,k24. 设恢复它们所需故障次数分别为N29,N28,··· ,N24.

令M= max{N30,N29,··· ,N24}, 由GOST 的密钥编排算法,M即为恢复主密钥所需故障次数.从以上攻击步骤可以看出, 每组密文对经过层层解密将参与到最后8 轮全部64 个半字节密钥的恢复中,恢复GOST 算法256 比特主密钥所需故障次数实际上为该64 个半字节密钥恢复所需故障次数的上界.

3.4 实验仿真结果和分析

通过计算机程序模拟3.3.4 节中的攻击方案, 设立恢复GOST 算法主密钥为一次完整实验, 其中每次实验的明文、密钥和故障具体位置均随机生成. 我们进行了一万次模拟实验来探寻该方法的攻击效果,图3 展示了GOST 算法单字节故障多轮攻击一万次模拟实验中恢复256 比特主密钥所需故障次数的分布情况, 结果表明12 次故障内成功恢复主密钥的实验占比达98%, 一万次实验成功恢复主密钥所需的平均故障次数为7.46, 相比现有的差分故障攻击结果有了很大的提升.

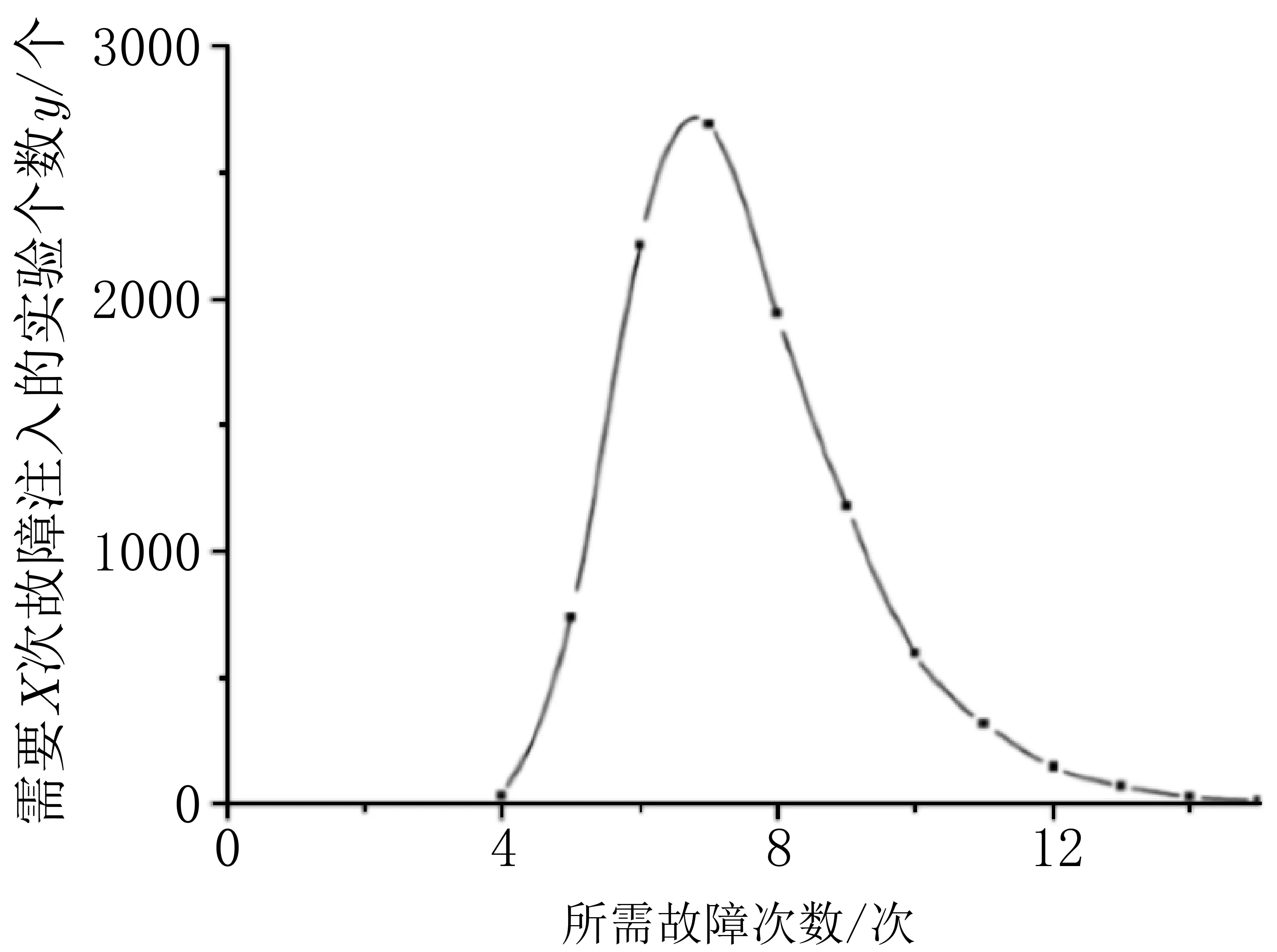
图3 GOST 一万次实验结果Figure 3 Result of 10 000 experiments on GOST

4 结束语

本文利用GOST 算法模加运算部件的特点, 采用差分故障对其进行了攻击. 通过在前22 轮任意一轮右侧输入处引入单字节随机故障, 较好地完成了GOST 的差分故障攻击. 实验结果表明, 完成GOST 的256 比特主密钥恢复平均所需故障注入次数为7.46, 一万次实验中有98% 的实验在12 次故障注入内即可完成主密钥恢复. 可见, 差分故障攻击对GOST 是十分有效的, 为了避免此类攻击, 需要对加密设备进行特别保护. 此外, 这种针对模加运算部件的攻击为同类型密码算法分析提供了新的思路, 也对模加运算相关算法的设计提供了新的参考.