借助数形结合思想解答物理难题

摘 要：物理作为高中教育体系中的一门重要学科，在新课程、新高考的评价体系下，随着知识难度与深度的提升，在解题训练环节，会遇到不少的难题，学生仅仅依靠简单的分析思考和计算很难应对，教师除讲授一些常规解题方法外，还需着重渗透数形结合思想，指导他们准确、高效的解答物理难题.笔者主要对如何借助数形结合思想解答高中物理难题进行分析与实践，并及时整理了一些实效性的教学对策.

关键词：数形结合思想;物理难题

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2021）22-0090-03

收稿日期：2021-05-05

作者简介：张金武（1971.7-），男，福建省连城人，本科，中学一级教师，从事高中物理教学研究.

“数”和“形”属于数学中两个最基本、最古老的研究对象，在一定条件下能够相互转化.数形结合思想还是一个十分常用的解题方式，其中在高中物理解题训练中，通常会出现部分难度系数较高的题目时，学生可借助数形结合思想来解答，不过关键还在于掌握扎实的物理基础知识，实现“数”和“形”的灵活转化，尽快找到切入点将解题过程简化，最终顺利求解.

一、变换物理难题图形，合理建立代数问题

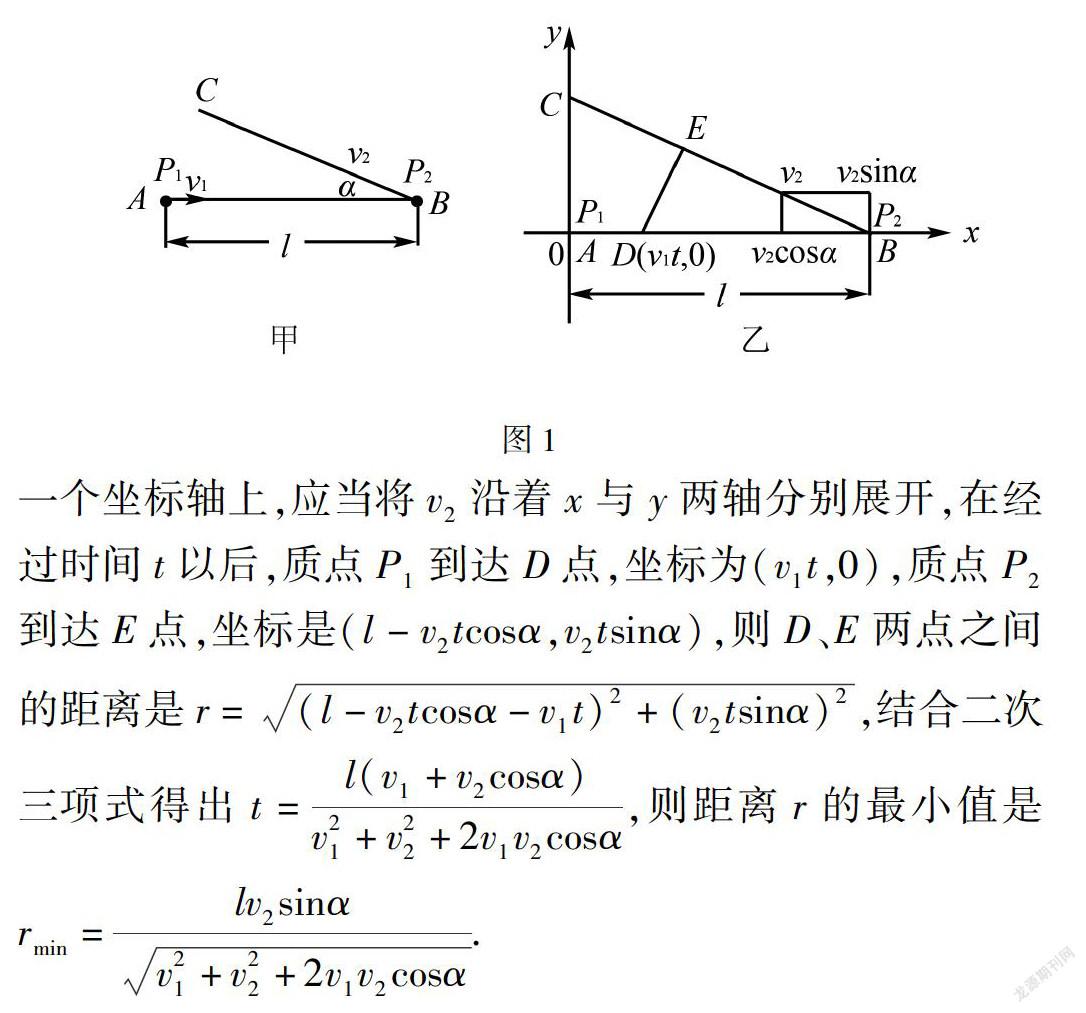
在高中物理解题教学过程中，仅仅提供一个现实中的物体图形，或者是描述某物体在运动状态下的一个示意图，这类题目看起来比较抽象，难度较大，学生一时之间很难很难找到突破口，极易陷入到困境当中，他们将会遇到解题瓶颈.解决这一类型的物理难题时，只依靠题目中的原图是无法求解的，高中物理教师应指引学生认真分析，把原图进行合理变换，得到描述物体运动过程中任一状态的图形，变成一个代数问题，帮助他们顺利解答难题.

处理这道题目时，学生应当它们竖直抛出后的运动情形在同一个平面直角坐标系中展示出来，如图4所示，让他们将这个代数问题顺利转变成图形问题，要想保证物体A与B相遇，应让两者具有一样的抛出位移，即为它们的图像在同一平面直角坐标系中应当具有交点存在.

解答过程如下：学生通过观察图形知道物体A第一次同物体B相遇的条件为物体B正好落在地面之上，即为Δt> tA-tB，而物体B抛出后的最迟状态为抛出的瞬间与物体A相遇，则Δt< tA（其中tA和tB分别表示A、B在空中的运动时间），综合分析得到：为保证物体A与B能够在空中相遇，Δt的取值范围应是2v0g<Δt<4v0g.

在高中物理解题教学中，针对难题的处理，教师应引导学生学会借助数形结合的优势分析和处理题目内容，将复杂化、抽象化的难题变得简单化、具体化，使其快速确定最佳解题方案与思路，不断增强物理解题和学习的信心，提高他们的解题水平以及物理核心素养.

参考文献：

[1]冯顺荣.数形结合思想在高中物理解題中的应用[J].高中数理化，2020（12）：38.

[2]严保华.数形结合思想在高中物理解题中的应用[J].数理化解题研究，2020（10）：61-62.

[3]赵为京.数形结合思想在高中物理解题中的巧妙应用[J].高中数理化，2020（06）：38.

[4]宋代强.高中物理解题中数形结合思想的应用探微[J].数理化解题研究，2019（19）：78-79.

[责任编辑：李 璟]