有效理答，让概念教学走向深入

檀秀春

课堂教学是师生之间、生生之间交往互动的过程，互动离不开对话，教师理答是师生交流互动中的重要环节。理答的本质是教师针对学生回答教学中的问题时产生的各种资源，积极地进行辨别、判断并加以恰当的、理性科学的回答。如果说有效提问能引发学生思考；那么有效的理答，学生能够明确问题的答案，反思自身的学习，体悟学习的进程，进而总结自己的收获。教师在课堂中恰如其分地把握好提问和理答，能够大大改善学习的进程，是有效教学的关键，两者缺一不可。同时，有效的理答，也是教师课堂素养的重要组成部分，直接体现了教师的课堂调控能力。

概念教学在小学数学教学中有着举足轻重的地位，数学概念以其语言精简、抽象、规范等特点与小学生心理特征、认识水平不相适应。为此，在概念教学中，教师更应重视课堂的理答，更好地促进学生对概念的掌握与理解。为此，在研究有效提问及预设的同时，应致力于研究如何让课堂理答充满智慧，让概念教学走向深入、高效。

一、追问式理答：打破沙锅问到底

追问式理答，就是在学生回答问题的基础上，教师进一步加以追问，追求问题的本源。教师适时的追问，可以增加探索问题的深度，避免学生流于问题的表面。同时，追问过程中，教师如能及时抓住孩子在回答过程中生成的一些资源，就能充分将其转化为学生学习探索数学知识、发展数学思维和体验数学思想方法的重要契机。

案例1：《百分数的意义》片断

师：课前我们已经让大家收集了一些百分数，现在请大家来说说你收集的百分数表示什么意思。

生1：我收集到的信息是：乐乐的投球命中率为41.3%。

师：这个41.3%表示什么意思？

生1：41.3%表示乐乐投了100个球，进了41.3个球。

教室里一片哗然。

教师示意大家安静，没有评价，继续将目光投向学生。

生2：怎么能有0.3个球，乐乐投要么是进41个，要么是进42个球。

生3：用近似值呀，乐乐投了100个球，大约进了42个球……

学生面面相觑，一时陷入困惑。

师：乐乐是不是只投了100个球？

生4：41.3%表示乐乐如果投了1000个球，进了413个球。

师：有道理吗？

孩子们点了点头，他们似乎觉得解决了0.3个球的问题。

师：刚才刘同学用“如果”这个词，用得非常好。大家想一想乐乐是不是刚刚好投了100个或1000个球？

生：肯定不是！

师：那么命中率41.3%这个数是怎么得到的？

片刻的思考后，学生豁然开朗，纷纷举起了手。

生5：41.3%这个数应该是表示乐乐投中球的个数除以投球的总数得到的结果，并不表示具体的投球个数，所以不能说投中了41.3个球……

“乐乐投球的命中率”是课堂上学生回答问题时生成的随机资源，教师通过第一次的提问，在学生应对的基础上层层深入追问，逐步引导学生弄清百分数概念的本质。教师通过理答，在学生学习的关键处，在思维的疑难处，在学习的最近发展区，进行了适当的点拨、合理的引领，从而使理答与提问有机地结合，形成一个整体，促进学生对概念的理解与掌握。

二、反证式理答：以子之矛攻子之盾

由于受小学生年龄特征、认知能力等因素制约，教材在揭示数学概念时，往往采用描述式。一些概念无法用严谨的语言来描述，学生理解起来有一定的难度，特别是一些是似而非的概念辨析，有时师生三言两语不一定就能讲得通。这时，教师可以应用反证理答加以说明解决。“以子之矛攻子之盾”“举一千个正例不如一个反例”，教师可以通过对概念、法则、定理、结论的反面情况进行研究论证，以求得问题的解决。

案例2：《商不变的性质》片断

教师出示竖式（如图1所示）：乐乐这样计算正确吗？为什么？

生1：正确，根据商不变的性质可知。

生2：正确，被除数和除数都同时除以100，商不变。

师：这一道题与我们前面学习的有没有什么不一样？

生3：好像前面学习的都没有余数，这个有余数……

教师没有评价，继续让他们讨论、辨析，他们说不出个所以然。

生4：老师，我们觉得是不对的，但又说不上来原因。

师：当我们正面没办法解决问题的时候，有时可以尝试从反面来思考、解决问题。我们可以假设这道题计算是正确的，那么根据乘除法的关系，可以怎样检验商是不是正确的？

生1：用“商×除数+余数=被除数”的方法来验证。

生2：如果16700÷200=83……1正确的话，那么200×83+1应该等于16700。

生3：200×83+1=16601≠16700，所以原来计算的结果是错误的。

师（继续追问）：那你们能说说正确的结果是多少吗？

生：正确结果应是16700÷200=83……100

本案例中，教师通过追问的方式，引导学生进行假设、反证，让学生排除思维定势的干扰，强化思维的批判性，进一步拓展学生思维的广阔性、敏捷性。

三、反問式理答：柳暗花明又一村

小学生以具体形象思维为主，逐步向抽象逻辑思维过渡，他们思考问题不会达到深刻、全面。他们对一些概念的理解，经常停留在字面上。教师面对学生这样的回答，应不予诊断性理答，而是沿着学生的思路进行假设、举例，让学生在自悟中加深对概念本质的理解。

案例3：《平行线》片断

师：什么样的两条直线是平行线呢？

生：永不相交的两条直线叫作平行线。

师：是不是两条直线只要不相交就一定是平行关系呢？（出示图2长方体框架模型）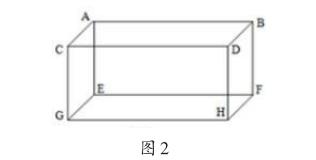

师：AB边和CD边会相交吗？

生：AB边和CD边不相交，它们是平行关系。

师：AB边和DH边会相交吗？

生：AB边和DH边不相交。

师：那它们也是平行关系吗？

生1：AB是横的，DH是竖的。

生2：因为它们的方向不一样，所以不是平行的关系。

生3：AB是在上面，DH是在前面，它们不在同一个面。

师：是不是不在同一个面的就一定不会平行？

生：不一定，AB和GH不在同一个面，但却是互相平行的。

师：非常好，AB和GH不在同一个面。（教师将一张长方形纸片放进框里）。

生：AB与GH不在同一个面，但现在都在长方形纸片上，可以看作是同一个面了。

师：像这种情况，我们可以说，AB和GH是在同一个平面内。那么，AB和DH有没有在同一个平面内？

……

该案例中，教师根据学生已有认知点，在学生的疑惑处适时反问，促进学生深入思考，逐渐明晰概念。

四、求同式理答：求同去异达共识

由于学生个体的差异，面对同一问题时，他们答案不一，有些是错误的。如果这些答案中有些信息与教师的预设内容又有共同点，教师对错误的信息不必急着否定。求同式理答，就是教师要引导学生去对信息进行筛选，分析其共同点，达到解决教学重难点的目的。在这个过程中，教师的理答就显得非常重要了。

案例4：《整数乘法运算定律推广到小数》片断

教师创设购物的情境，让学生求一共要花多少钱。先分步列式，最后再根据分步算式要求学生列出综合算式（教师板书后如图3所示）。

师：两个算式表示两种不同的解题思路，可以用等号连接，这种情况类似于咱们学过的哪些知识点？

生1：乘法结合律

生2：乘法分配律

师：其他同学的意见呢？

（学生大部分都赞同这两位同学）

师：看来意见比较统一，那么正确答案是什么呢？先想一想，乘法分配律和乘法结合律都属于哪个知识点呢？

生：运算定律。

师：对，我们就是运用了运算定律。至于具体哪个运算定律，大家有异议，看来是知识被遗忘了。我们一起来复习一下运算定律。

理答的本质是一种师生对话，既是一种教学行为，也是一种教学评价。理答形式可以是语言方式，还可以是动作、表情等肢体方式。上面所阐述的方式只是概念教學中一些常用的理答方式。有效的理答与有效的提问是相辅相成的。教师的有效理答，体现了教师个体的教学技巧与素质，直接影响着对课堂的调控程度，决定着课堂教学的效率，只有讲究策略的理答才能提高我们的课堂效率。