基于AMESim的电动车辆线控液压转向控制策略研究与试验分析*

2021-09-13常江雪鲁植雄

中国农机化学报 2021年8期

常江雪，鲁植雄

(1.江苏经贸职业技术学院智能工程技术学院，南京市，211168；2.南京农业大学工学院，南京市，210031)

0 引言

随着物联网技术、5G信号传输技术的发展，消费者对智能汽车、自动驾驶的需求逐渐增强，电动车辆自动驾驶技术也已成为了研究的热点。新能源汽车产业发展规划明确到2025年，新能源汽车新车销售量占比达20%左右[1-2]，可以说，电动汽车或电动车辆将是关键发展方向。自动转向技术或线控转向技术是电动车辆自动驾驶技术的关键技术环节，该技术也将是智能车辆的关键技术配置。如今，机械液压技术较为成熟，关键还是控制系统及控制策略的可靠性、精准性、安全性，因此，有必要充分研究电动车辆线控转向控制策略，把握控制系统的可靠性、安全性等的量化指标，助力电动车辆转向控制技术发展。

转向控制方式主要有机械式、液压助力式、电控液压助力式、电动助力式、线控转向式五种形式[3]。综合来看，线控转向系统的整体结构可以分为三类，分别是前轴转向、前后轴转向、四轮独立控制转向，依据转向执行机构的不同，前轮线控转向系统又可分为线控电动转向系统[4-5]、线控液压转向系统[6]。控制策略是控制性能的核心。综合来看，应用于线控转向系统中的控制算法主要有PID控制、优化PID控制、滑模控制、模糊控制等[7-8]。宋效文[9]基于滑模控制建立了评判标准，对比PID控制与滑模控制从而得出在滑模控制下前轮转角更具有稳定性。刘秋杨[10]基于粒子群优化算法对分数阶PID进行了整定参数优化，鲁棒性和控制精准度较好。王玉源[11]针对优化LADRC控制器参数的DE算法步骤进行参数自寻优设计，有较好的加载电机电流环控制性能。何浩然[12]针对低速时的比例控制策略与高速时的模糊控制策略进行仿真试验验证，表明控制策略均有较好的控制性能，较为稳定安全。

路感的加载是线控转向系统的关键技术，通常路感的加载主要通过获取速度、侧向加速度、方向盘转动速度及扭矩、轮胎侧向力等信息，综合相位补偿、阻尼补偿、惯量补偿和摩擦补偿等计算路感电机控制信号，精准控制电机输出至减速机构并反馈到方向盘，实现路感扭矩的加载[13-14]。何浩然[12]通过模拟传统汽车方向盘获得路感的方式进行路感模拟，并在控制器内部设计路感补偿，使汽车获得极佳的路感。Ait-oufroukh N等[15]建立了驾驶员方向盘力反馈动力学模型，用液压转向执行机构转向阻力的动力学响应特性与转向机构的传动比来设计路感反馈。谢有浩等[16]通过电机加载，纳入转向阻力矩、转向摩擦力矩、转向阻尼力矩以及限位力矩。

为进一步研究电动车辆线控液压转向系统的控制算法，优化线控转向性能，本文将建立电动车辆线控液压转向系统数学模型，基于AMESim软件进行动力学仿真分析，并进行台架试验，分析系统响应性、抗干扰性能，优化控制算法。

1 线控液压转向控制系统设计

1.1 系统整体结构及工作原理

系统主要由方向盘及路感系统、控制系统、液压系统、转向机构等组成，系统机构如图1所示，工作原理如图2所示。工作时，驾驶员控制方向盘转动，控制系统通过转角传感器获取方向盘转动幅度信号，控制系统根据控制算法输出控制信号至液压系统，油缸随之执行伸缩运动，进而推动转向机构，最终传输至轮胎，轮胎随之转动，实现方向盘转动指令的执行。

图1 电动车辆线控液压转系统结构组成Fig.1 Structure composition of electric vehicle hydraulic drive by wire system

图2 电动车辆线控液压转系统工作原理Fig.2 Working principle of electric vehicle hydraulic drive by wire system

该过程中存在两个闭环控制，一个是轮胎转角与方向盘转角的闭环控制，工作时，控制系统会实时读取轮胎转角信号并与方向盘转角进行偏差计算，经计算输出控制信号，不断消减偏差，实现角度的闭环控制。另一个是路感模拟机构中加载电机加载扭矩与实际路感的闭环控制，路感控制器读取加载电机加载扭矩与实际路感信息，并计算二者偏差，反馈至控制器，进而调整电机控制指令，调整加载扭矩，逐渐消减偏差至最低。

本系统主要有三个特点。一是增加了路感模拟机构，该机构采用电机加载的模式，结构简单，易操控。二是采用前轮线控转向，前轮转向技术成熟，且双轴线控转向或四轮线控转向机构较为复杂，成本较高，适用于专用电动汽车，常规的电动乘用车、商用车、农业机械等更适用前轮转向。三是采用液压系统执行转向操控。液压转向系统较为成熟，抗冲击性好，较为稳定。

1.2 液压系统设计

液压系统需要实现油缸方向、压力、流量的精准控制，且可靠性要高，同时考虑到线控转向系统精简结构、降低重量等设计目标，因此本系统在保证系统功能、性能的基础上，尽量减少液压系统部件的增加。本系统控制阀选用了控制精度高、可靠性高的电液比例换向阀，同时为了保证系统在紧急情况下安全性，系统增设了溢流阀。总体来看，系统结构简捷，成本适宜，抗冲击性好，较为稳定可靠。

液压系统如图3所示。系统主要由溢流阀、电液比例阀、双作用油缸、油泵、单向阀、减压阀、油箱、油滤、变量泵等组成。该系统主要有三个特点：一是采用双作用油缸与电液比例换向阀结合实现左右转向，直线行驶或非转向时，油缸行程处于中间位置，转向时电液比例换向阀切换至左侧或右侧，实现油缸换向；二是基于变量泵的闭心式系统，中立时，油泵输出的液压油不再经过换向阀，通过变量泵实现流量的控制同时保持一定的压力，待转向时可以快速建立工作压力，提高响应速度；三是增加了安全保护阀，主要是进油路的溢流阀、单向阀，溢流阀用来控制进油口的压力，单向阀防止负载的突然增加破坏油泵。其次，回油路设置了减压阀，可防止负载过大或回油压力过大损坏油箱。

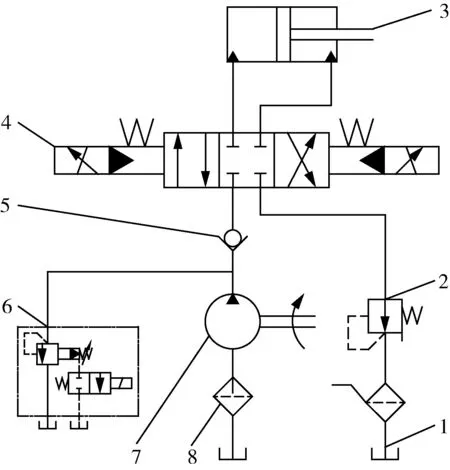
图3 电动车辆线控液压转向系统的液压系统设计Fig.3 Design of hydraulic system for electric vehicle material by wire hydraulic steering system1.油箱 2.减压阀 3.双作用油缸 4.电液比例阀 5.单向阀 6.溢流阀 7.油泵 8.油滤

1.3 路感加载系统设计

综合考虑电机加载、阻尼油缸加载、励磁电机加载等方式，本系统选用较为可靠稳定的电机加载方法，系统结构如图1所示。加载系统的主要执行部件为加载电机及减速机构，工作的指令来源于系统控制器，工作时，控制器实时采集整车行驶速度、方向盘转动速度、转动扭矩、液压缸工作压力等信号，同时纳入相位、摩擦等补偿系数，最大化接近实际路感。具体详见路感系统数学建模部分介绍。

2 基于AMESim的数学模型建立

2.1 整体模型设计

数学模型是量化分析的关键。传统建模方法，主要是根据系统工作原理及外部影响因素等情况列出系统数学关系式，并进行频域时域的稳定性分析，优化控制参数[10]。对于该系统来说，其包含液压系统、机械系统、电机控制系统，较为复杂，且存在两个闭环控制，建立完整的数学模型较为复杂，且会有较多的假设、设定，影响了仿真的效率。事实上，本系统的关键还在于液压系统，对于液压系统来说，影响系统的因素较多，为此，本文选用了AMESim进行建模仿真，其拥有较准确的液压模块，同时可纳入其他系统的数学模型以及加入PID控制器[17-19]。仿真模型如图4所示，其主要有方向盘及路感加载模块、液压系统、转向执行机构及反馈模块、PID控制器四个部分。

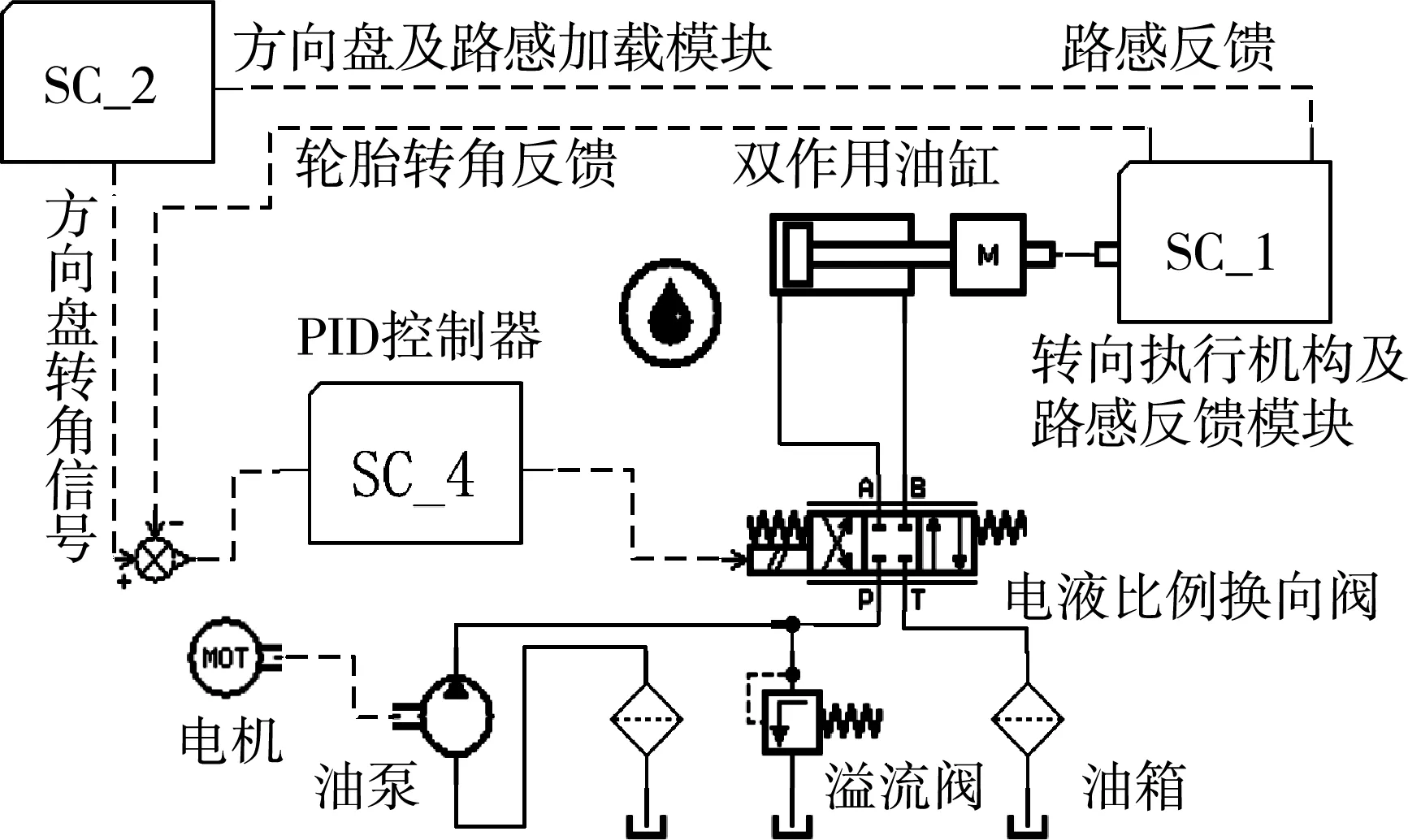
图4 电动车辆线控液压转向系统仿真模型Fig.4 Simulation model of hydraulic steer by wire system for electric vehicle

2.2 执行机构动力学数学模型

根据轮胎行驶时的动力学理论，将轮胎转向时的受力分析如图5所示，转向时轮胎主要受力有支撑反力Fd，前轴压力Ff，转向回正力Fh，地面摩擦力Fm，所受转向相关的扭矩主要有摩擦扭矩Tm，转向加速度扭矩Ta，回转扭矩Th，以及转向拉杆的转向扭矩Tz[20]，如图5所示。

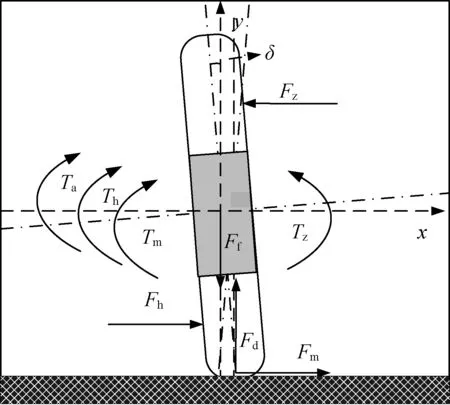
图5 轮胎受力分析Fig.5 Force analysis of tire

根据上述受力及动力学分析，结合AMESim的自带仿真模块，设计执行机构动力学数学模型如图6所示。

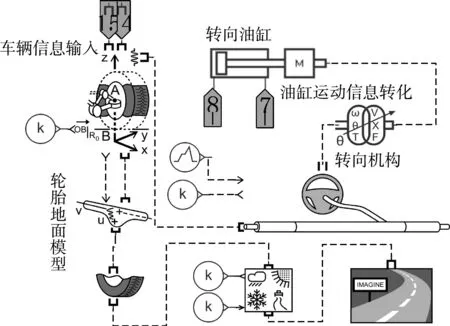
图6 转向执行机构仿真模型Fig.6 Simulation model of steering actuator

2.3 传动比数学模型

传统转向系统工作时，方向盘转到一个角度，车轮就会随之等比例转动，该比例由其机械或机械液压传动系统决定，扣除轮胎气压、液压系统温度影响下的液压油密度等因素影响，趋于固定。但是在线控转向系统中，传动比可由电控系统调整，可跟根据行驶速度、转向阻力等职能调整[21-22]。为提高车辆操纵的稳定性，于蕾艳[23]计算出变传动比公式，本文参照该模型。

(1)

式中：iSBW——理想传动比；

k1——前轮的侧倾刚度；

k2——后轮的侧倾刚度；

a——前轮的轴距；

b——后轮的轴距；

v——车速；

m——整车质量；

l——整车长度；

i——传动比。

经过参数的核算，本文将其换算成与速度变化的线性函数。

2.4 路感数学模型

AMESim内置电机模型，因此路感的建立关键在于确定路感的影响因素，获取路感加载扭矩的数学模型。基于学者的研究基础，可以发现，路感扭矩的源于轮胎行驶中的受力情况，以及考虑到行驶安全等因素的扭矩补偿，为此得出路感加载扭矩数学模型如下。

Tf=Td+Tm+Ta+Th+Tv

(2)

式中：Tf——路感加载扭矩；

Td——基础扭矩；

Tm——摩擦补偿扭矩；

Ta——转向角加速度补偿扭矩；

Th——回转补偿扭矩；

Tv——行驶速度补偿扭矩。

Td=Kdm

(3)

式中：Kd——恒定扭矩系数；

m——整车质量。

Td是基础扭矩，也就是在无反馈无补偿的情况下的加载扭矩，与整车质量相关，解决无其他补偿的情况下仍具有一定的转向阻力，等同于传统传动机构的传动阻力。

Tm=μMf

(4)

式中：μ——摩擦补偿扭矩系数；

Mf——前轴质量。

补偿的是转向时轮胎与地面之间的摩擦阻力带来的扭矩，与前轴质量与摩擦系数相关。

Ta=Mfr2α

(5)

式中：r——转向力矩半径；

α——转向角加速度。

该扭矩补偿是对应转向时加速产生的反馈扭矩。

Th=KhMfδ

(6)

式中：Kh——补偿回转扭矩系数；

δ——外倾角。

主要是补偿转向时的回转扭矩，因为前轮有外倾角及侧倾角，转向时会有回转力矩。

Tv=KvV

(7)

式中：Kv——补偿速度扭矩系数；

V——行驶速度。

Tv主要是与速度相关，速度越快，转向扭矩越大。

基于上述模型建立了AMESim线控液压转向系统路感模拟仿真模块如图7所示。

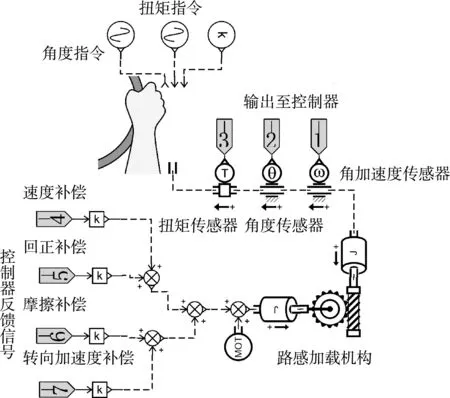
图7 路感加载仿真模块Fig.7 Road sense loading module

3 控制器设计及控制策略仿真分析

3.1 PID控制控制器设计

PID控制算法较为稳定可靠，但是在一些非线性多参数系统当中，固定的PID参数不能有效的应对多种工作状态[24]，一些学者设计模糊PID控制器、或自适应PID控制器，等有效的解决了适用性问题。为了优化PID在不同路况及行驶模式下的适用性，本系统设计了自适应调整比例P参数的优化PID控制器。综合分析，本系统比例P参数的自适应调整主要考虑到高速状态下安全性以及大转向角度的快速反应，因此，控制器增加了车速调整参数K1及转向幅度调整参数K2，用来调整不同车速下及转向幅度下的PID控制器响应时间[25-26]，控制器工作原理如图8所示。

图8 液压线控转向自适应PID控制器Fig.8 Adaptive PID controller for hydraulic steer by wire

3.2 控制系统性能响应分析

阶跃信号响应。设定方向盘全行程转向角度1 000°，左右各500°，也就是各方向分别近一圈半，对应前轮最大转向角为40°，仿真试验时，为方便查看响应情况，将方向盘转向角度等效成轮胎转向角度，也就是左右转向范围0°～500°等效成0°～40°。分别设定左转5°、35°右转5°、35°，设置成阶跃信号，观察系统响应情况。通过多次反馈调整，响应情况如图9所示，右转5°响应时间0.2 s，右转35°时间为0.9 s，左转5°时响应时间0.3 s，左转35°响应1.3 s，系统响应无超调，左转时由于转向机构的影响，阻力稍大，影响了响应时间。

正弦信号响应。正弦信号，也就是稳定左转至最大角度，然后右转至最大角度，最后回正至零点，查看系统跟踪情况，分别设定两个频率，周期分别是5 s与10 s，如图10、图11所示，5 s周期下，响应误差略大，但是基本在3°以内，10 s周期跟踪较好，基本在2°以内，无明显超调，较为稳定。

图10 5 s周期的正弦信号响应Fig.10 A sinusoidal signal with a period of 5 seconds

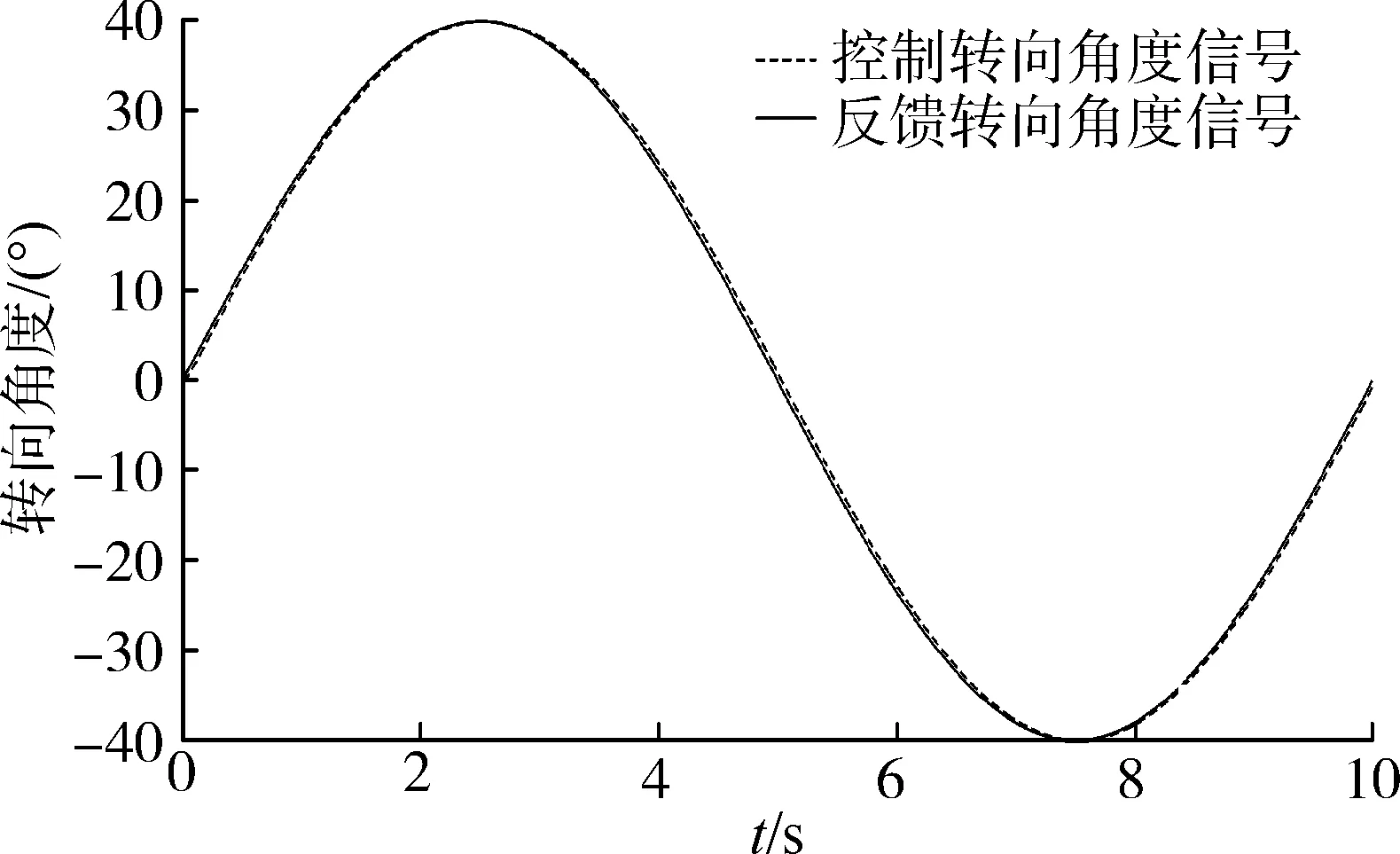
图11 10 s周期的正弦信号Fig.11 A sinusoidal signal with a period of 10 seconds

3.3 控制系统抗干扰能力分析

在正弦响应情况下，设定一组干扰信号，也就是增加转动阻力，查看系统抗干扰能力。10 s正弦控制信号周期内，分别设定4个干扰信号，分别在2 s、5 s、8 s增加干扰阻力200 N·m、400 N·m、800 N·m，响应情况如图12所示，扭矩干扰下，跟踪偏差在3°以内。可以发现，在干扰起始阶段电磁阀快速响应，油缸压力快速建立，能够稳定过渡。

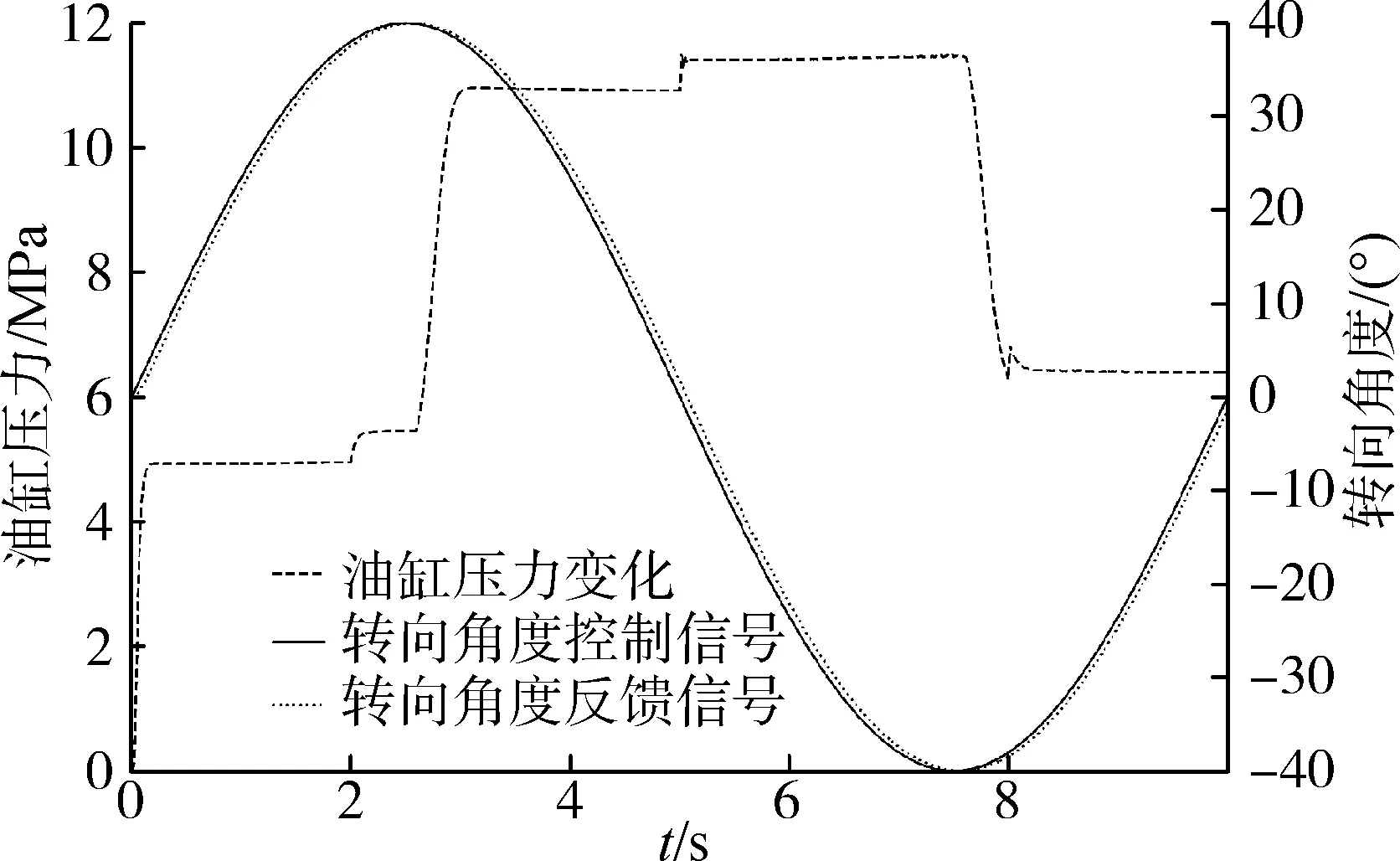
图12 抗干扰能力响应Fig.12 Response of anti-jamming

4 试验验证

4.1 试验台架及数据采集程序

基于上述设计及仿真分析情况，课题组设计了试验台架，如图13所示。

图13 电动车辆线控液压转向系统试验台架Fig.13 Test bench for electric vehicle steer by wire hydraulic steering system

试验台架主要是有底盘、方向盘及路感模拟机构、液压执行机构、转向梯形机构、轮胎以及相应的传感器等，基于上述仿真分析，课题组就液压系统、转向系统、加载系统等硬件进行了反馈调整。同时，基于LABView虚拟系统设计了一套数据采集程序，可适时采集方向盘转角、轮胎转角、油缸液压压力、液压温度等信号。试验时，根据各试验要求分别向转向电机输入控制信号，控制转向机构转向，此时，采集系统实时采集转向机构执行信号及轮胎转向信号，在此基础上，课题组就控制信号与反馈信号进行偏差计算，进而分析系统控制性能。

4.2 响应性验证

通过控制电机输出周期为10 s正弦信号，控制方向盘转动，分别通过转角传感器采集方向盘转角信号，通过主销上安装的编码器采集轮胎转角信号，响应情况如图14所示，图中将方向盘转角进行了等效计算，方便与轮胎转角对比。可以发现，正弦响应性较好，跟踪偏差在3.2°以内。

图14 响应性验证试验Fig.14 Response verification test

4.3 稳定性验证

为了考察系统的稳定性，系统设置了转向角快速变化的跟随试验。在10 s的运行周期内，分别在0 s、4 s、8 s快速转动方向盘，其中在0 s处转向角由0°在2 s 内转至右方向20°，在4 s处由右转20°在2 s内转至左转30°，转向幅度50°，8 s时由左转30°转至右转30°，幅度达60°，如图15所示。试验表明，转向角快速变化下，跟随偏差在4°以内，系统快速响应情况基本良好，稳定性较好。