扫描信号激振下振动器-大地耦合动刚度和动阻尼研究

2021-09-13徐光明黄志强

工程设计学报 2021年4期

李刚，徐光明，黄志强，亓文，郝磊

（1.西南石油大学机电工程学院，四川成都610500；2.中国石油集团东方地球物理勘探有限责任公司，河北涿州072750）

油气勘探与开发在很大程度上依赖于勘探技术和装备，勘探技术和装备的水平决定了找油找气的能力和准确度。可控震源具有高效、环保、安全等优点，被誉为油气勘探领域的工程利器，已应用于石油天然气的勘探［1-3］。

振动器是可控震源的核心部件，直接决定了可控震源所激发信号的质量。目前广泛采用的振动器的激振模型是20世纪80年代Sallas提出的加权和模型［4］。近年来，很多学者通过分析和测试指出，由于没有考虑频率变化对振动器平板与大地之间相互作用的影响，加权和模型只在较窄的频宽下适用，随着激振信号频率的提高，采用加权和模型计算出的振动出力与实际出力的误差越来越大［5-7］，已经难以满足勘探要求。因此，迫切需要建立适用于扫频激振的振动器-大地耦合模型，而其核心问题是准确描述在扫频激振下振动器平板与大地之间的相互作用。对此，国内外学者展开了诸多研究。

Wei［8-9］建立了包含电控系统、液压系统和机械系统的可控震源仿真模型，并将仿真分析结果与现场测试结果作了对比研究，认为振动器平板与大地之间的相互作用因地表环境的不同而不同。Tinkle 等［10］检测了井下检波器的数据后指出，不能用简单的模型描述振动器平板与大地之间的相互作用关系。Dean等［11］采用薄膜式压力传感器和井下检波器对振动器和大地的振动响应作了测试，认为振动器平板与大地之间的相互作用远比想象的复杂。Noorlandt等［12］分析了振动器平板与大地之间的接触状况，认为该接触状况对振动器的动态响应影响很大，提出采用多组自由弹簧来描述平板与大地之间的接触。2018年，Wei等［13］通过现场测试分析了振动器在软地、沙地和硬地的激振效果，结果表明振动器在不同地表上的激振效果不同。

随着可控震源研究及应用的深入，研究人员认识到振动器-大地耦合振动对振动器的输出信号起着至关重要的作用，随即开始探索振动器-大地的耦合作用。刘洪斌等［14］开展了可控震源的动态分析，指出将大地模型简化为简单的加权和弹性阻尼系统有较大的误差。庄娟等［15］建立了电磁可控震源-大地耦合模型，用土介质的弹性系数和阻尼系数描述振动器平板与大地之间的作用关系，分析了耦合系统的幅频特性。其研究发现：随着平板质量的减小，平板振动幅度增大，土介质的受力幅度也增大；在相同的激振条件下，地表不同，则大地的受力不同。徐爱军等［16］提出采用质量-弹簧-阻尼器受迫振动来描述可控震源平板-大地振动系统，分析表明，平板振动向大地的传输非常复杂，振动系统有可能会出现谐振。黄志强等［17］通过有限元仿真，分析了振动器平板-大地的接触性质与能量传递的关系，结果表明，在不同的接触性质和激振频率下平板向大地传递的能量不同。2018年，马磊等［18］通过试验分析了振动器的振动响应与激振频率的关系，表明振动器的输入与输出信号存在明显的相位差且其随频率的提高而增大。

鉴于加权和模型存在计算误差大等不足，研究人员提出应该建立新的模型来描述振动器平板与大地之间复杂的作用关系，且已经认识到激振频率和地表属性会对振动器-大地耦合振动产生影响，但尚未具体分析在不同扫描频率下平板与大地之间的相互作用。为此，本文基于弹性半空间理论，构建振动器-大地耦合振动模型，研究在不同扫描频率下振动器-大地耦合动刚度和动阻尼，分析它们的影响参数和影响规律，以进一步掌握平板与大地之间相互作用的机理，为实现振动器的高精度激振提供理论指导。

1 振动器-大地耦合振动模型的构建

1.1 扫描信号

可控震源如图1所示，振动器的结构如图2所示。

图1 可控震源Fig.1 Seismic vibrator

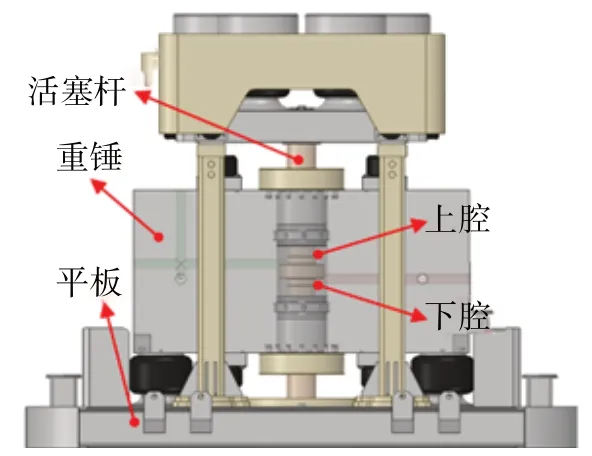
图2 振动器的结构Fig.2 Structure of vibrator

在振动器的重锤和活塞之间存在相互隔离的上腔和下腔。当振动器激振时，高压液压油交替进入上腔和下腔，推动重锤上下运动，同时重锤的反作用力作用在活塞杆端面上，通过与活塞杆固连的平板传递给大地，从而产生地震信号。推动重锤运动的液压力也称为扫描信号。扫描信号的瞬时幅值和频率都是时间的函数。扫描信号瞬时幅值Q（t）的表达式为：

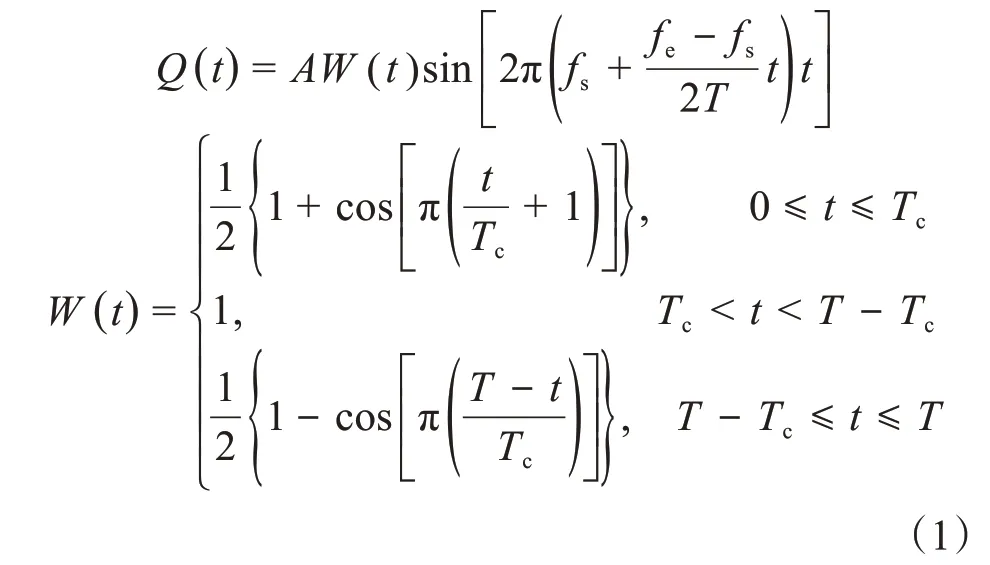
式中：A为液压力的额定幅值；W（t）为余弦窗口函数；fs为扫描起始频率；fe为扫描终止频率；t为扫描时间，0 ≤t≤T，T为扫描持续时间；Tc为窗口长度。

当A=250 000 N，fs=5 Hz，fe=105 Hz，Tc=0.5 s，T=10 s时，扫描信号如图3所示。

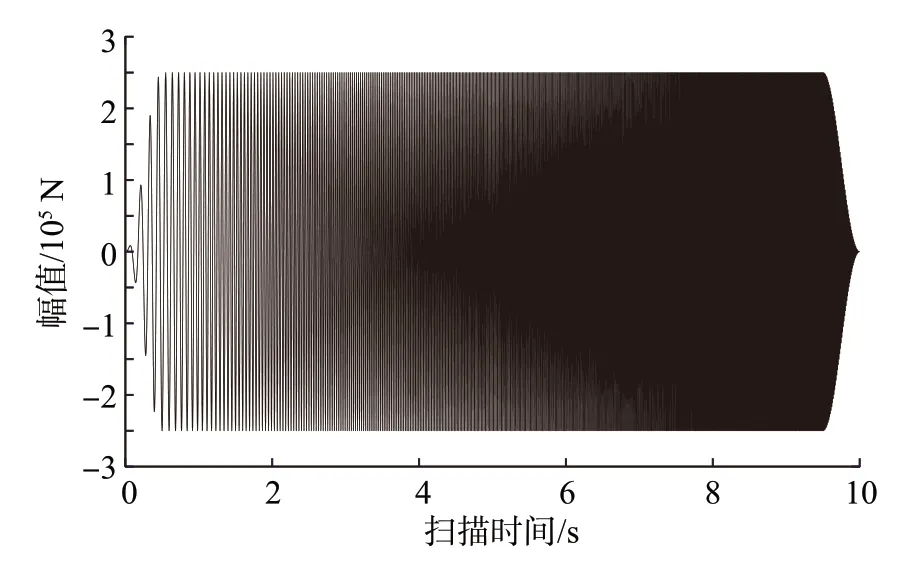
图3 扫描信号Fig.3 Sweep signal

1.2 振动器-大地耦合振动模型

扫描信号的频率不是固定的，而是随着时间呈线性变化，这就大大增大了激振的复杂性，也是加权和模型不能准确描述振动器-大地耦合振动的根本原因。为准确描述平板与大地之间的相互作用关系，须突破传统思维，引入新的、可靠的理论，而广泛应用于动力基础研究的弹性半空间理论为解决这一问题提供了思路。

弹性半空间理论广泛应用于土木工程研究。其基本假设是大地为弹性、均匀、各向同性的半无限空间体，用弹性模量和密度等参数来描述大地的力学性质，分析动力基础在大地上的振动［19-20］。动力基础在大地上的振动与平板在大地上振动的基本原理是一致的，这为分析平板与大地之间的相互作用提供了理论依据。

根据弹性半空间理论建立的振动器-大地耦合振动模型如图4所示，振动器平板与大地之间的作用如图5所示。其中：mr和mb分别为重锤和平板的质量；wr和wb分别为重锤和平板的位移；Ko和Co分别为液压刚度和液压阻尼；Kz和Cz分别为平板与大地之间的动刚度和动阻尼；Q0ei（ωt+φ）为作用在平板上的外力；P0eiωt为平板作用在大地上的力，R0eiωt为P0eiωt的反作用力；ω为平板的角频率；φ为初相位。

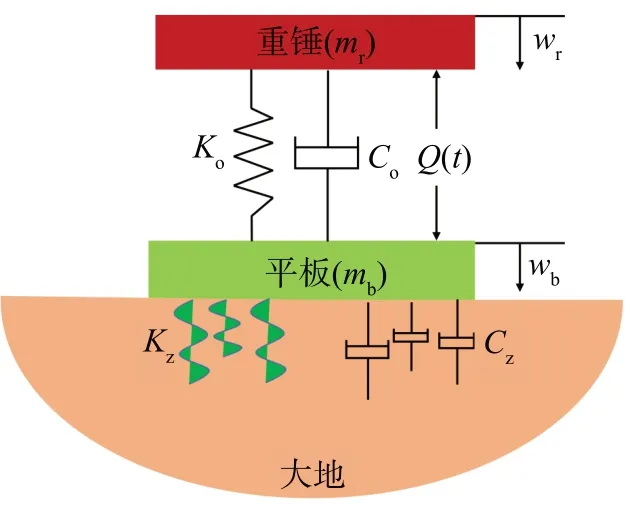
图4 振动器-大地耦合振动模型Fig.4 Vibrator-ground coupling vibration model

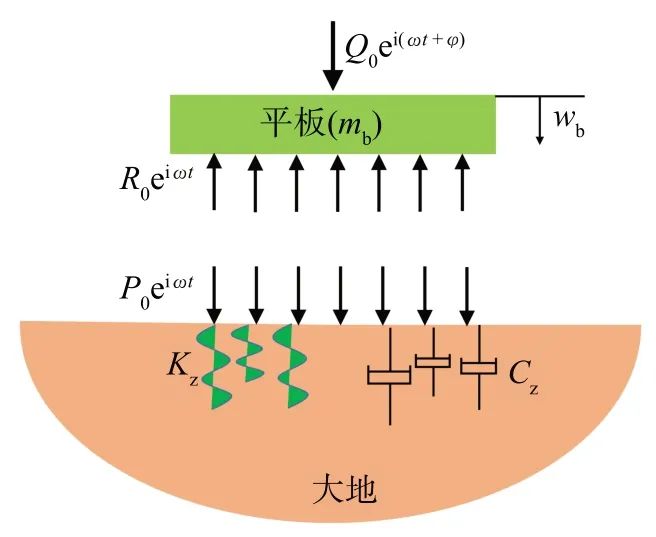
图5 振动器平板与大地之间的作用示意Fig.5 Schematic of interaction between vibrator plate and ground

由图5可得平板的动力学方程为：

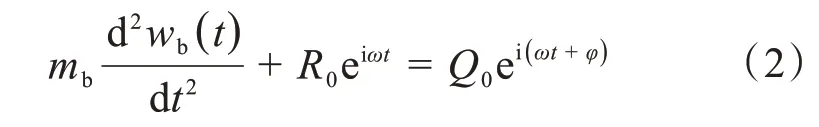
设平板上任意一点到平板中心的距离为r，则该点的垂直位移wb（r，0）的汉克尔变换wb（p，0）为［21］：

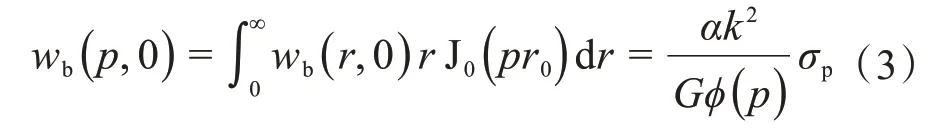
式中：p为第一类贝塞尔函数作无穷级数展开的级数；J0（pr0）为零阶第一类贝塞尔函数，其中r0为平板等效半径，为平板底面积；a和k均为与频率相关的因变量系数，分别体现了纵波波速和横波波速在频率变化时对位移的贡献，，其中vp和vs分别为纵波波速和横波波速；G为土壤剪切模量；ϕ(p)为瑞利方程；σp为平板作用在大地表面的压强，其表达式为：

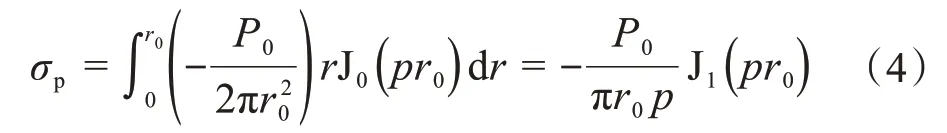
通过汉克尔变换，实现了垂直位移的积分变换，将其变为可积，并引入了频率这一关键变量。

由汉克尔反演求平板的垂直位移，可得：

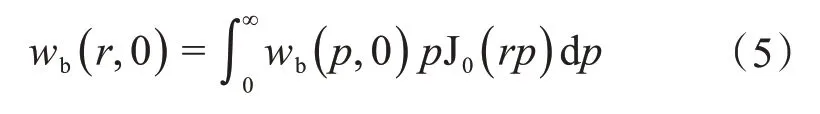
将式（3）和式（4）代入式（5），可得：

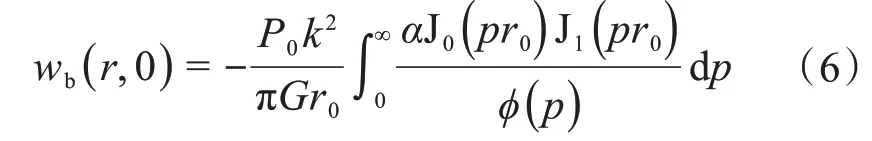
假设平板与大地耦合良好，平板的位移可以等效为平板中心点的位移，则平板的位移为：

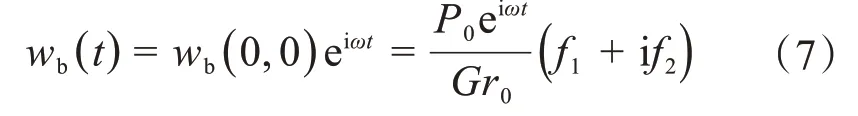
式中：f1和f2均为无量纲频率a0的函数［22］，表示位移与频率之间的关系，其中为土壤密度。

对于弹性材料，其剪切模量G与弹性模量E的关系为：，其中μ为泊松比。

f1和f2可分别表示为：

则P0eiωt和R0eiωt可分别表示为：

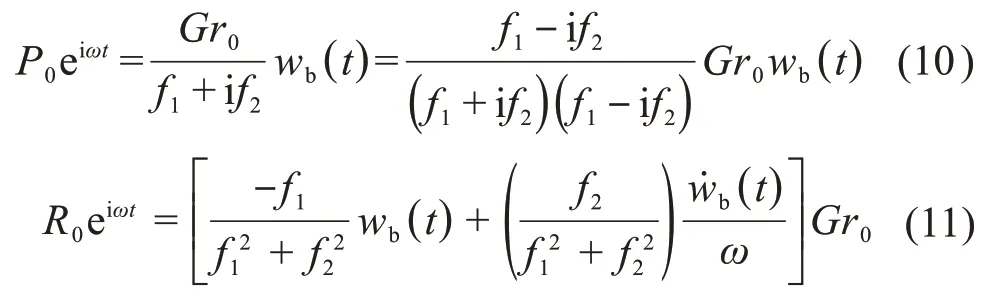
所以，式（2）可改写为：

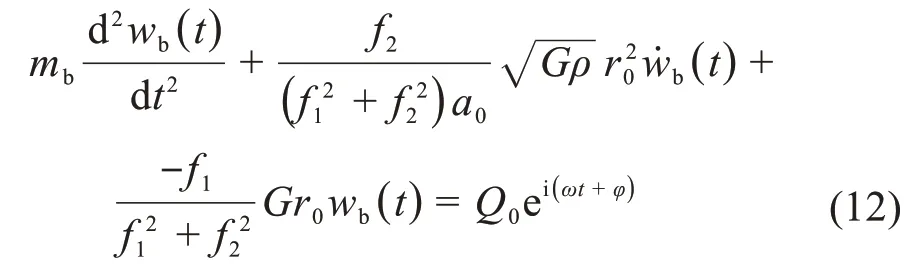
平板与大地之间的动刚度Kz和动阻尼Cz可以表示为：

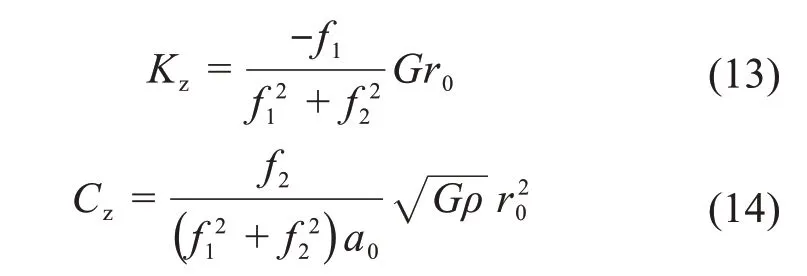
最后，可得重锤和平板的动力学方程分别为：

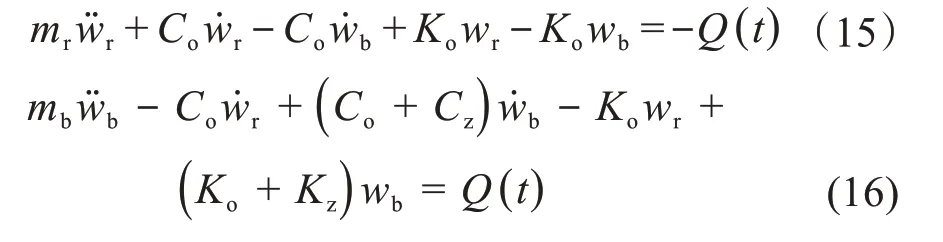
2 试验验证

2.1 试验方案

为了验证所构建的耦合模型的准确性，进行重锤加速度响应测试。通过单频扫描和线性扫描激振，对比分析在单频扫描和线性扫描下重锤的加速度响应。试验所用的仪器主要包括1 台可控震源、1 套Force-III振动控制系统、1套重锤加速度传感器和数据采集器等。重锤加速度传感器如图6中方框所示。重锤加速度响应测试中的扫描参数如表1所示。

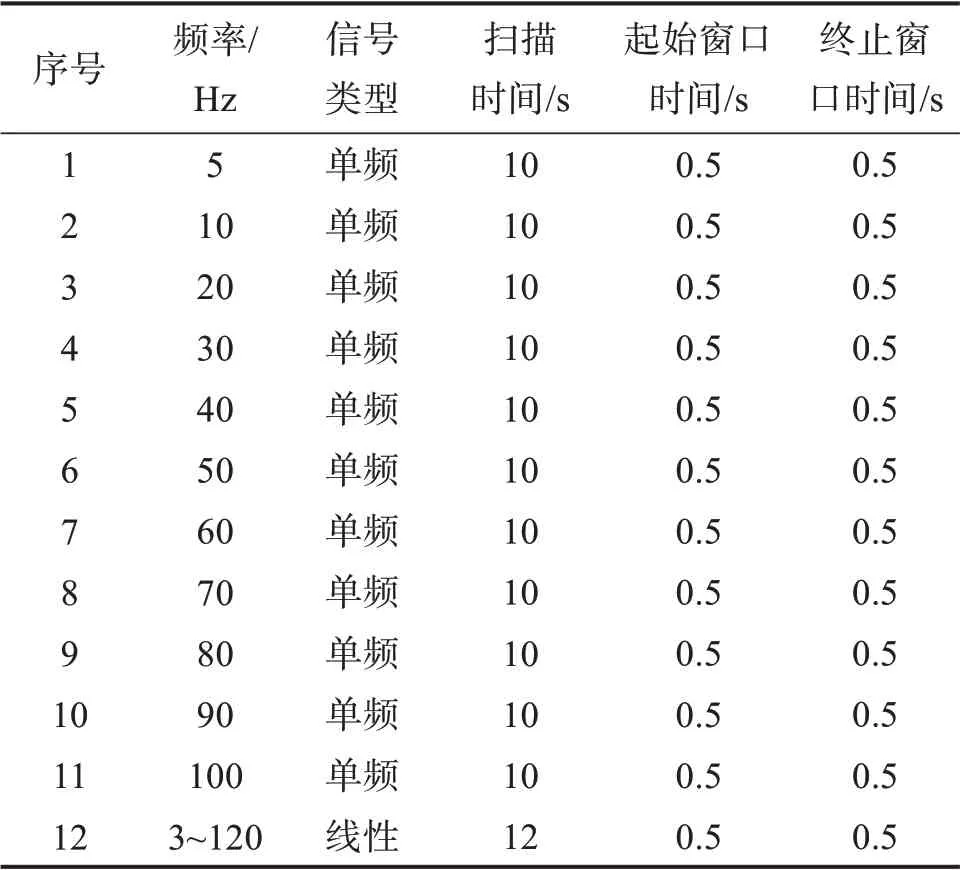
表1 重锤加速度响应测试中的扫描参数Table 1 Sweep parameters for test of acceleration response of heavy hammer

图6 重锤加速度传感器Fig.6 Acceleration sensor of heavy hammer

重锤和平板的结构参数和土体参数如表2所示。将参数代入式（15），可以求得重锤加速度。通过对比重锤加速度的计算值和测试值，来验证仿真模型的准确性。

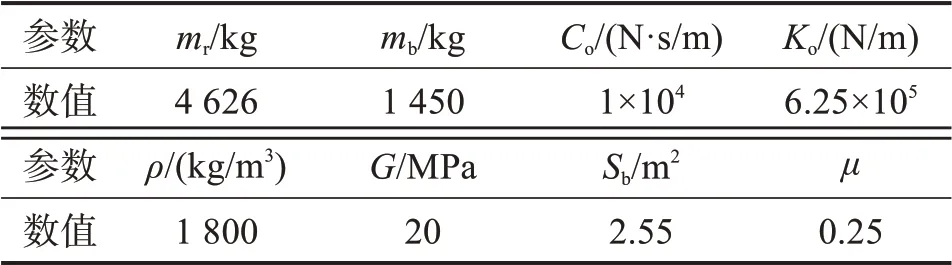
表2 重锤和平板的结构参数和土体参数Table 2 Structural parameters of heavy hammer and plate and soil parameters

2.2 试验结果

重锤加速度计算值与测试值的对比如图7所示。为便于对比，对线性扫描信号激振下的重锤加速度进行频域分析。

由图7（a）可知，在单频扫描信号激振下，重锤加速度的计算值与测试值基本一致，两者的最大误差为8.66%，表明构建的耦合模型能较好地描述重锤在单频信号激振下的响应运动。因在计算时没有考虑重锤偏心运动的影响和液压系统的干扰，加速度响应很规律且没有噪声和畸变，而测试中在各起始阶段加速度均有明显的畸变，加速度出现了独立的突变峰值。由图7（b）可知，在线性信号激振下，重锤加速度的计算值与测试值的变化趋势是一致的，都呈先增大后减小再逐渐增大。在10 Hz附近，加速度都达到了第1个增大阶段的最大值，且测试值的峰值略大于计算值的峰值；在随后的减小阶段，计算值稳定地减小，而测试值出现了不规律的波动，这可能是液压系统的噪声和干扰导致的；在第2个增大阶段，计算值与测试值增大的趋势和幅值均吻合较好，仅测试值有小幅波动。以上结果表明耦合模型对在线性信号激振下的振动响应也有较好的适应性和准确度，可以用来描述扫描信号激振下振动器-大地的耦合作用。

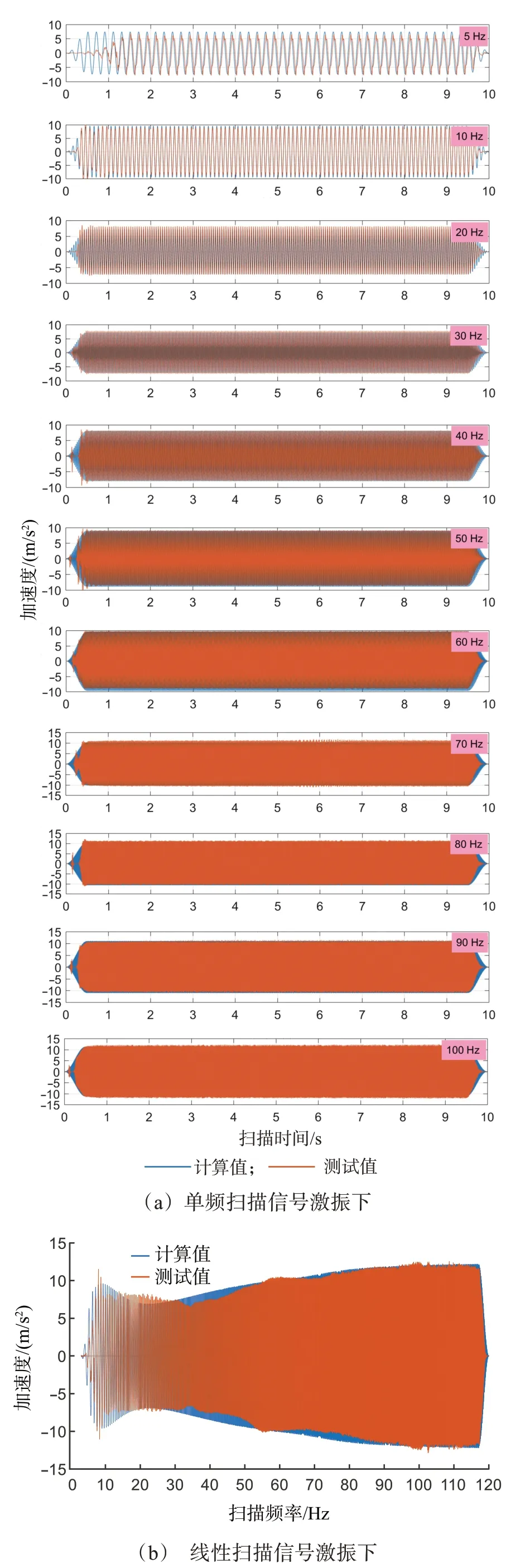
图7 重锤加速度计算值与测试值的对比Fig.7 Comparison between calculated and measured accel‐eration of heavy hammer

3 耦合参数对动刚度和动阻尼的影响

根据式（13）、式（14）和表1，可以算得动刚度和动阻尼随扫描频率的变化曲线，如图8所示。随着频率从3 Hz提高到120 Hz，动刚度从2.903×108N/m加速下降到1.812×108N/m，动阻尼也随着频率的提高而减小，但减小的幅度相对较小，仅从7.460×105N·s/m减小到7.221×105N·s/m。这表明，平板与地面之间的相互作用随着频率的提高而减弱。一方面，平板作用在地面上的力将会减小，另一方面，地面对平板的限制将减弱。当平板与大地之间的相互作用减弱时，振动器产生的下传信号的强度和信噪比必然会降低，从而影响高频信号的勘探效果。而从目前的勘探需求来看，高频成分是进行地震反演所必不可少的，因此必须加强振动器与大地之间的相互作用。因此，掌握影响动刚度和动阻尼的耦合参数具有重要意义。

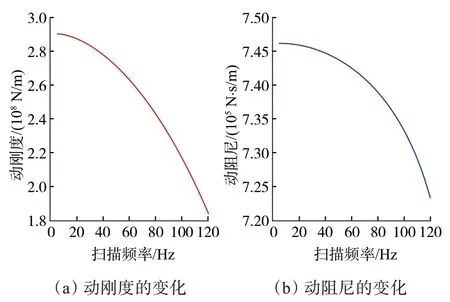
图8 动刚度和动阻尼随扫描频率的变化曲线Fig.8 Variation curve of dynamic stiffness and dynamic damping with sweep frequency

3.1 耦合参数分析

由图4可知，耦合参数主要包括扫描频率、大地弹性模量、土壤密度、平板底面积、液压油刚度、液压油阻尼、扫描信号的额定幅值、平板质量和重锤质量。其中：液压油的刚度和阻尼由液压油本身决定，其值基本不变，不纳入考虑；扫描信号的额定幅值可人为设定，且其对加速度的影响较为单一，即额定幅值越大加速度越大，且在现场作业时一般将它设置为固定值，故也不纳入考虑。由式（13）和式（14）可知，影响动刚度和动阻尼的耦合参数有扫描频率、大地弹性模量、土壤密度和平板底面积。为了便于纵向对比各参数的影响能力，对各参数进行等比例取值，即以表2中的参数值为基数，分别取其0.50，0.75，1.00，1.25，1.50的倍值进行分析。扫描频率范围为3～120 Hz。

3.2 大地弹性模量的影响

大地弹性模量对动刚度和动阻尼的影响如图9所示。由图9（a）可知：随着扫描频率的提高，动刚度逐渐减小；大地弹性模量与动刚度也基本成正线性关系，随着大地弹性模量等比例减小，动刚度等间隔减小。大地弹性模量每增加0.25 倍，动刚度的增加量约为0.73×108N/m。由图9（b）可知：随着扫描频率的提高，动阻尼逐渐减小；大地弹性模量与动阻尼也成正相关关系，但是随着大地弹性模量等比例增加，动阻尼的增幅越来越小。从土壤软硬度来看，较硬（弹性模量较大）的土壤与平板之间的相互作用更强，更有利于力的传递。

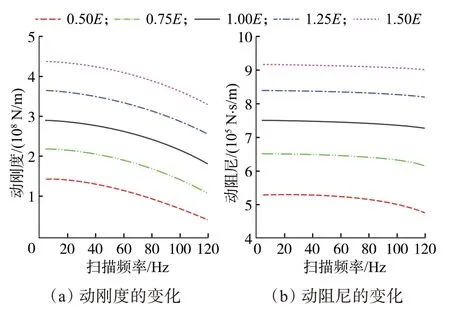
图9 大地弹性模量对动刚度和动阻尼的影响Fig.9 Effect of soil elastic modulus on dynamic stiffness and dynamic damping

3.3 土壤密度的影响

土壤密度对动刚度和动阻尼的影响如图10所示。由图可知，土壤密度对动刚度的影响与对动阻尼的影响截然不同。在3～10 Hz的低频阶段，5条动刚度随扫描频率的变化曲线基本重合，土壤密度对动刚度的影响很小。随着频率提高，动刚度减小；土壤密度越大，动刚度越小。

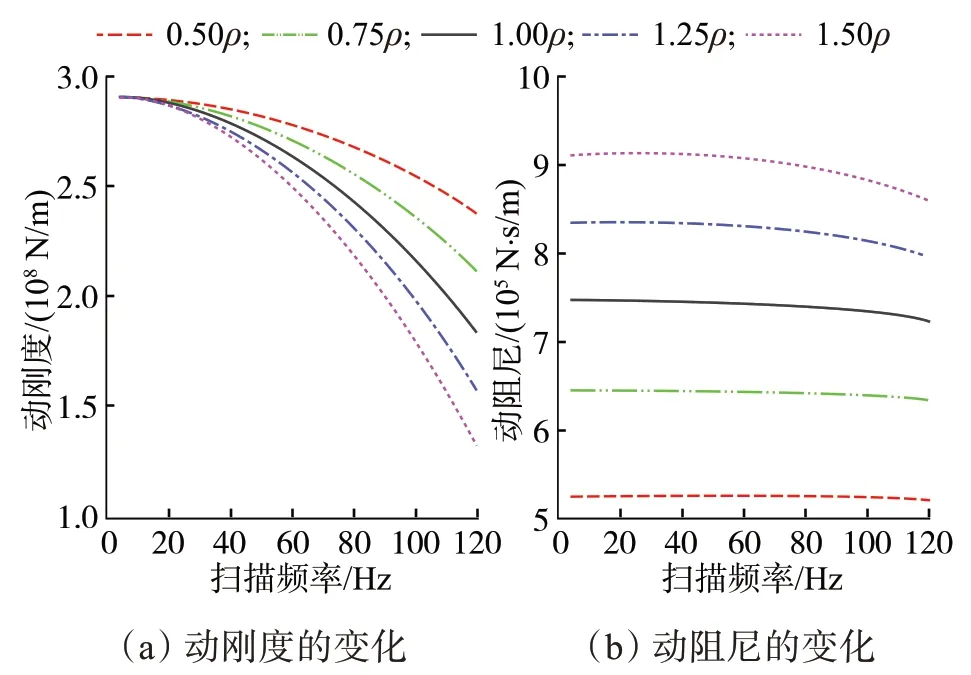
图10 土壤密度对动刚度和动阻尼的影响Fig.10 Effect of soil density on dynamic stiffness and dy‐namic damping

土壤密度越小，越有利于振动出力。土壤密度与动阻尼的关系同大地弹性模量与动阻尼的关系类似，两者也成正相关关系，且随着土壤密度等比例减小，动阻尼减小的幅度增大。动阻尼较大意味着对能量的耗散能力较强，即土壤会消耗较多的下传能量。

3.4 平板底面积的影响

平板作为可控震源与大地耦合的媒介，其底面积决定了可控震源与大地之间作用的范围，对动刚度和动阻尼都有很大的影响。平板底面积对动刚度和动阻尼的影响如图11所示。由图11（a）可知：随着频率提高，动刚度减小，表明平板与大地之间的相互作用会减弱；当频率小于100 Hz时，平板底面积与动刚度基本成正相关，随着频率提高，加大平板底面积对增大动刚度的作用越来越小；当频率大于100 Hz后，较小的平板底面积所对应的动刚度反而更大一些。这表明不能一味依靠加大平板底面积来加强平板与大地之间的相互作用，当频率上升到一定值后，其相互作用反而会减弱。由图11（b）可知：在任一扫描频率下，平板底面积与动阻尼基本成线性关系；平板底面积越大，动阻尼越大，对系统的能量耗散能力则越强。

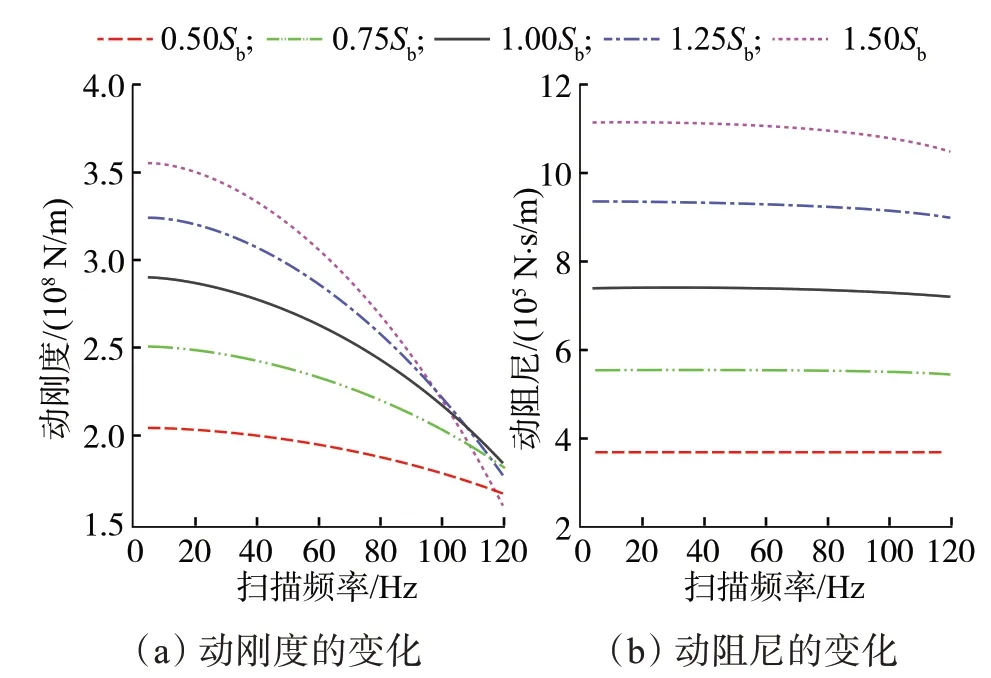
图11 平板底面积对动刚度和动阻尼的影响Fig.11 Effect of plate bottom area on dynamic stiffness and dynamic damping

由上述分析可知：大地弹性模量对动刚度和动阻尼的影响最大，在扫描频宽内大地弹性模量与动刚度和动阻尼均基本成线性关系；随着土壤密度和平板底面积等比例增大，其对动刚度的影响随着扫描频率的提高呈现渐变的趋势，土壤密度对动刚度的影响逐渐增大，而平板底面积对动刚度的影响逐渐减小；土壤密度和平板底面积的等比例增大对动阻尼的影响基本一致，其值越大，动阻尼越大，且近似成等比例关系。