基于FUNWAVE-TVD模型的岸礁次重力波数值模拟

2021-09-13冯卫兵华伟豪

河海大学学报（自然科学版） 2021年4期

冯卫兵，华伟豪,2，张俞,2

(1.河海大学港口海岸与近海工程学院，江苏南京 210098； 2.河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098)

岸礁海岸是一种典型的珊瑚礁海岸，主要分布于南北回归线之间的热带海洋，在我国的海南岛和雷州半岛沿海分布广泛。岸礁地形主要由陡峭的礁前斜坡、水深较浅且相对平坦的礁坪及礁后斜坡组成，礁前斜坡与礁坪连接处为礁缘，发育成熟的礁坪宽度通常几百米至几千米不等。波浪是影响和塑造岸礁海岸最重要的海洋动力因素之一[1]，当深海波浪传至礁前斜坡时，由于该区域内水深急剧变化，波浪经浅水变形在礁缘附近破碎并损耗大量能量，破碎后波浪继续沿礁坪向岸传播，此过程中受礁坪底摩阻的影响波能进一步耗散，最终到达岸线处的高频短波能量很小，此处波浪动力一般由频率较低的次重力波主导[2]。次重力波频率位于0.004～0.04 Hz之间，其生成机制主要包括两种：(a)Longuet-Higgins等[3]提出的约束波机制，即由波浪差频作用形成的伴随波群传播的二阶次谐波，其幅值在向岸入射过程中随水深减小幅值逐渐增长，并在短波破碎后从波群释放成为自由长波[4]；(b)Symonds等[5]提出的破碎点移动机制，入射波高的变化导致破碎点在垂岸方向振荡，随时间变化的辐射应力梯度在破碎带内生成向岸与离岸的自由长波。次重力波是岸礁海岸的形成、发育和演变的主要动力之一，因此研究岸礁海岸的次重力波的生成与传播规律具有非常重要的意义。

早期对于岸礁海岸的波浪研究以现场观测和物理模型试验为主，随着计算机技术的发展，数值模拟成为研究该问题的主要方法之一。van Dongeren等[6]采用基于非线性浅水方程的Xbeach模型分析了带有潟湖的Ningaloo岸礁上的次重力波运动；Ma等[7]采用基于N-S方程的非静压模型NHWAVE研究了次重力波波高及能量在岸礁地形的沿程变化；Pelez-Zapata等[8]采用非静压模型SWASH研究了短波与次重力波在礁后斜坡的爬高。由于Boussinesq模型兼顾了计算效率与精度，可模拟波浪的非线性与色散性，因此近年来被广泛应用于珊瑚礁地形的波浪数值模拟中，如Nwogu等[9]采用任意水深层Boussinesq模型捕捉到了礁坪末端低频波的一阶共振放大现象；Su等[10]将激波捕捉法应用于完全非线性的Boussinesq模型FUNWAVE-TVD,研究了岸礁底摩阻与礁坪水位等对次重力波的影响，随后诸裕良等[11]应用该模型模拟了不规则波在岸礁上的传播过程，分析了礁坪宽度、礁后斜坡坡度对礁坪传递波高和爬高的影响；Ning等[12]进一步总结了水位与地形等条件对次重力波爬高的影响；Yao等[13]利用高阶非线性Boussinesq模型结合现场观测资料研究了实际尺度下岸礁地形的次重力波的生成并分析了其在礁坪上的激发模态。

从已有研究来看，以往利用Boussinesq模型对岸礁地形次重力波的数值模拟研究多涉及波高与波浪爬高，对非线性能量传递过程涉及较少；考虑到次重力波存在多种生成机制及其较高的反射系数，采用相关性分析区分各重力波分量在时域上的传播过程对研究岸礁地形的次重力波运动尤为重要。本文在岸礁地形不规则波物理模型试验数据验证的基础上，采用FUNWAVE-TVD模型3.4版本分析了次重力波在岸礁地形的生成、传播及相关的能量演变过程。

1 数值模型简介

FUNWAVE-TVD模型是特拉华大学开发的完全非线性的Boussinesq数值模型，该模型基于由Chen[14]建立的控制方程：

ηt+∇·M=0

(1)

uα,t+(uα·∇)uα+g∇h+V1+V2+V3+Rf+Rs=0

(2)

数值模型控制方程采用有限体积法和有限差分法进行离散，对色散项使用有限差分法处理，其他项使用有限体积法求解；时间积分采用较为稳定的Runge-Kutta法确定自适应时间步长，利用CFL准则保证计算收敛；计算过程结合HLL近似黎曼求解器计算数值通量、高阶MUSCL-TVD法求解界面通量。

FUNWAVE-TVD模型在模拟波浪破碎过程中可采用激波捕捉法将波高水深比作为判断波浪破碎的阈值，通过关闭色散项将方程退化为非线性浅水方程模拟波浪破碎过程，但其模拟结果可能造成对礁坪上次重力波频段波能的显著低估[10,12]。本文采用改进后的在控制方程中添加人工涡旋黏性项的方法[15]模拟波浪破碎时能量的耗散，人工黏性项Rbx表达式为

(3)

其中ν=Bδb2(h+η)ηtP=(h+η)u

式中：ν——黏性系数；P——水平动量流；δb——混合长度系数，δb=1.2；u——水质点水平速度；B——黏性项启动系数，根据自由波面对时间的偏导数ηt控制该项开启或关闭，表达式为

(4)

式中：Cbrk——破碎参数；ηt，I——破碎起始阈值，当ηt≥ηt，I时，波浪破碎开始；ηt，F——破碎终止阈值，当ηt<ηt，F时黏性项为0，破碎终止。

FUNWAVE-TVD模型可对固边界、动边界和吸收边界进行模拟。模型固边界时令固壁处法向速度、波面法向梯度及切向速度法向梯度都为0；动边界采用干湿网格法进行处理；吸收边界通过设置海绵层实现，海绵层采用Larsen等[16]直接衰减型与摩阻型的组合，前者令海绵层内变量φ(即u,η)在每个时间步长直接发生衰减：

φ=φ/Cs

(5)

式中：Cs——衰减系数；n——网格数；αs、γs——参数，用于控制衰减系数随网格的变化率。摩阻型海绵层直接采用模型中的底摩阻项加以处理，数值模型中通过在动量方程中添加底摩阻项的方法模拟底摩阻的影响：

Rf=-Cduα|uα|

(6)

式中：Cd——底摩阻系数。

2 模型验证

2.1 物理模型试验简介

为了验证FUNWAVE-TVD模型对岸礁地形波浪传播数值模拟的适应性，采用Demirbilek等[17]在密歇根大学进行的风浪水槽物理模型试验数据验证模型。该试验在长35 m、宽0.7 m、深1.6 m的水槽中进行，如图1所示，x为距礁缘水平距离，地形剖面由复合坡度的礁前斜坡、4.8 m宽的礁坪和1∶12的礁后斜坡组成，礁坪对应z=0 m高程，礁坪与槽底的垂直距离为0.5 m，岸礁模型表面为相对光滑的PVC材质。造波机距礁前斜坡坡脚15.5 m，入射波基于随机相位的JONSWAP谱生成，谱峰增强因子为3.3。自造波机向岸沿程8个测点(G1～G8)处布置的波高仪用于记录波面时间序列，测点距礁缘水平距离分别为-5.91 m、-5.72 m、-5.39 m、-1.12 m、-0.58 m、0 m、2.17 m和4.34 m位置，采样频率均为20 Hz。

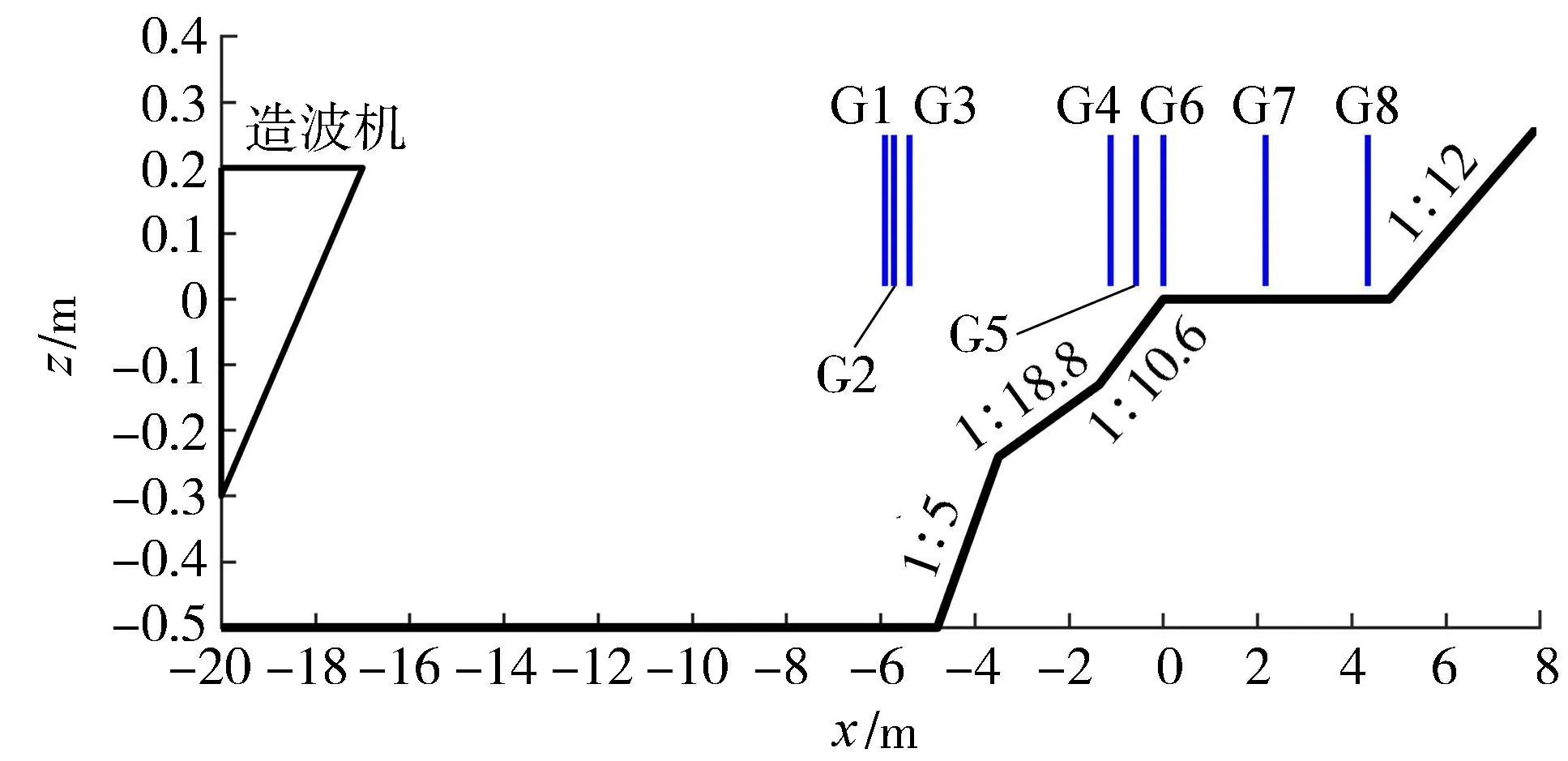
图1 物理模型试验设置Fig.1 Experiment setup of physical model

2.2 参数设置

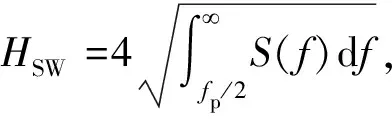
表1 入射波工况

(7)

式中：N——测点数；xm——试验值；xp——模拟值。I越接近1说明模型精度越高。

2.3 参数敏感性分析

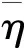
取破碎参数Cbrk=0.40、0.55、0.70分别进行数值模拟计算，结果如图2所示。3种工况下短波有效波高的模拟值与试验值吻合均较为良好，谱峰周期较小时短波传至礁前斜坡时已开始耗散且无显著的浅化成长。次重力波有效波高在礁前斜坡有所增长，在礁坪上呈波动状，并随入射波谱峰周期增大而增大。模型对礁前常水深处次重力波波高有所高估，但礁坪上模拟值与试验值吻合较好，模型较合理地模拟了次重力波波高的沿程变化。Test45中，时均水位的模拟值与试验值吻合较好，其余两种工况下模拟值较试验值偏大。破碎参数取不同值时，礁坪上次重力波有效波高有所变化，但对模拟结果总体影响较小。

图2 不同破碎参数条件下参数试验值与模拟值空间分布对比Fig.2 Spatial distribution comparison of measured and predicted results with different breaking parameters

取底摩阻系数Cd=0.001、0.005、0.010、0.015分别进行数值模拟计算，结果如图3所示。底摩阻系数对短波影响较小，礁坪上短波有效波高随底摩阻系数增大有轻微下降；次重力波有效波高对底摩阻系数变化敏感，随底摩阻系数增大而减小，由于礁前常水深处部分次重力波能量来自礁后斜坡反射的次重力波，因此此处波高也受底摩阻系数影响较大；时均水位对底摩阻系数变化基本不敏感。总体而言，底摩阻系数取0.005或0.010时岸礁上次重力波有效波高模拟值与试验值吻合更好。

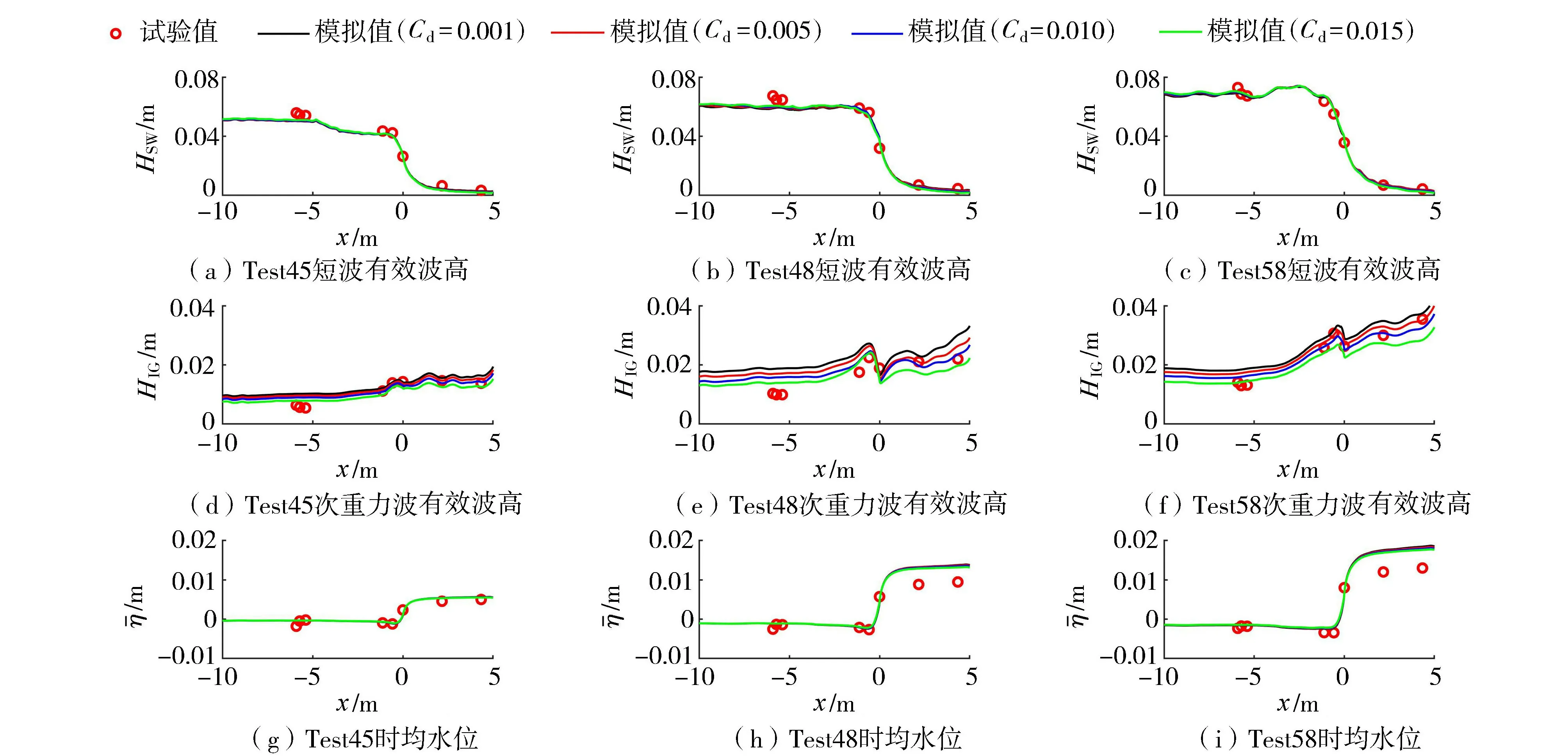
图3 不同底摩阻系数条件下参数试验值与模拟值空间分布对比Fig.3 Spatial distribution comparison of measured and predicted results with different friction coefficients

表2为破碎参数与底摩阻系数取不同值时由式(7)计算的短波、次重力波有效波高和时均水位的模拟精度，模型对于短波有效波高的模拟精度均可达到0.9以上，次重力波有效波高与时均水位模拟精度受入射波要素影响较大且后者对破碎参数与底摩阻系数变化基本不敏感。结合图2、3分析认为Cbrk=0.55、Cd=0.010时，数值模拟结果更为理想，3组试验次重力波有效波高模拟精度分别为0.83、0.74和0.91。

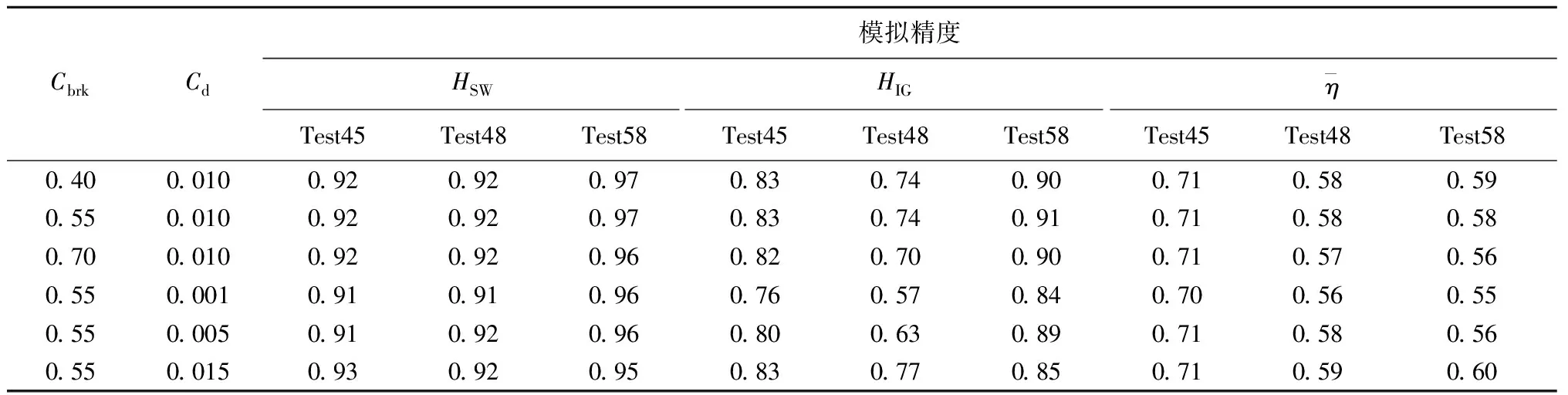
表2 不同参数下数值模型的模拟精度

3 次重力波的传播过程与波能演变

采用前面验证后的数值模型，仍基于Demirbilek等[17]的试验(未专门指明时均以Test48为例)对次重力波的生成与传播及相关的波能演变进行分析。

3.1 次重力波的生成与传播

次重力波在近岸的两种生成机制均与短波波群有密切的关系，可通过互相关分析的方法研究次重力波运动规律[4]。以两组时域信号X(t)与Y(t)为例，归一化后的互相关系数为

(8)

式中：τ——信号在时域上的延迟；σX、σY——X(t)、Y(t)的标准差；〈〉——时间平均。相关系数RXY(τ)代表两组时域信号在不同时间延迟上的相关程度，取值在-1～1之间，绝对值越大，两组信号相关性越强。对短波包络与次重力波波面时间序列进行互相关分析，并通过二者相关性在时域与空间域的分布可推知短波作用下次重力波的生成与传播过程。次重力波波面时间序列可直接由低通滤波得到，短波包络A(t)为

A(t)=|ηhf(t)+Hil{ηhf(t)}|lf

(9)

式中：Hil——希尔伯特变换算子；下标hf、lf分别表示高通滤波(f>0.5fp)与低通滤波(f<0.5fp)。

对Test48的模拟结果进行互相关分析。图4(a)为测点G2处的短波包络与沿程各点次重力有效波波面序列的互相关分析结果，黑色虚线对应测点G2位置，白色实线对应τ=0。测点G2在τ=0时存在一负相关峰，向岸靠近时该相关峰对应的时域延迟τ逐渐增大，对应入射的约束波，由于约束波波谷与波群包络的波峰对应，因此与短波包络呈负相关性，该相关峰幅值在礁前常水深处较小，在礁前斜坡上有显著的增强。x≈0 m处，在τ≈5 s时出现的向岸正相关峰与离岸的负相关峰分别对应破碎点移动机制激发的向岸与离岸的次重力波，前者在τ≈12 s时传递至岸线处并在礁后斜坡反射，因此礁坪上次重力波有效波高呈驻波形态。入射的约束波相关峰在礁缘处消失，未能传至礁坪上，可能在礁缘处反射或随短波破碎而耗散。Su等[10]对于非平直礁坪地形的互相关分析显示，高水位时约束波可传递至礁坪末端，而本工况中相对淹没水深较小，因此礁坪上次重力波的生成由破碎点移动激发机制主导。在τ>20 s时礁缘离岸一侧可以观察到向岸传播的正相关峰与反射的正相关峰的叠加，根据该相关峰对应的时域延迟，可能是破碎点激发的离岸次重力波在边界发生了二次反射，模型中海绵层未能充分吸收离岸的长波。总体而言，数值模型较准确地模拟了两种生成机制激发的次重力波在岸礁地形上的运动趋势，与Pomeroy等[20]基于现场观测的分析结果基本符合。

图4 短波包络与次重力波互相关分析结果Fig.4 Cross-correlation analysis results between short-wave envelopes and IG wave motions

图4(b)为沿程各点短波包络与相应位置的次重力波波面时间序列互相关分析结果，在礁前常水深处约束波负相关峰始终处于τ=0处，说明此时约束波与短波波群以相同速度传播。随着水深减小，该相关峰逐渐偏离白色实线出现在τ>0的一侧，说明传播过程中约束波的波谷逐渐滞后于短波包络的波峰。

图5对比了试验值与模拟值在测点G2处短波包络与其他部分测点次重力波信号的互相关性，模拟结果中两种生成机制激发的次重力波对应的相关峰，在时域上出现的时间及各自演化趋势与试验结果基本吻合。此外测点G2试验值在τ≈20 s时可观察到一向岸传播的负相关峰，该峰出现的时间约等于离岸的负相关峰以浅水波速传递至造波机处并反射回测点G2所需的时间，因此该相关峰为二次反射的长波，而数值模型在造波源后设置了海绵层，因此二次反射波的相关峰在时域上出现略滞后于试验值，模拟结果显示该相关峰反射过程中由负相关变为正相关，在Su等[10]的研究成果中也同样发现该现象，因此模拟结果中测点G2在τ≈24 s时离岸的正相关峰与二次反射的正相关峰在此处叠加，相关性较试验值更强，可能与礁前常水深处(测点G1～G3)次重力波有效波高的模拟值较试验值偏大有关。

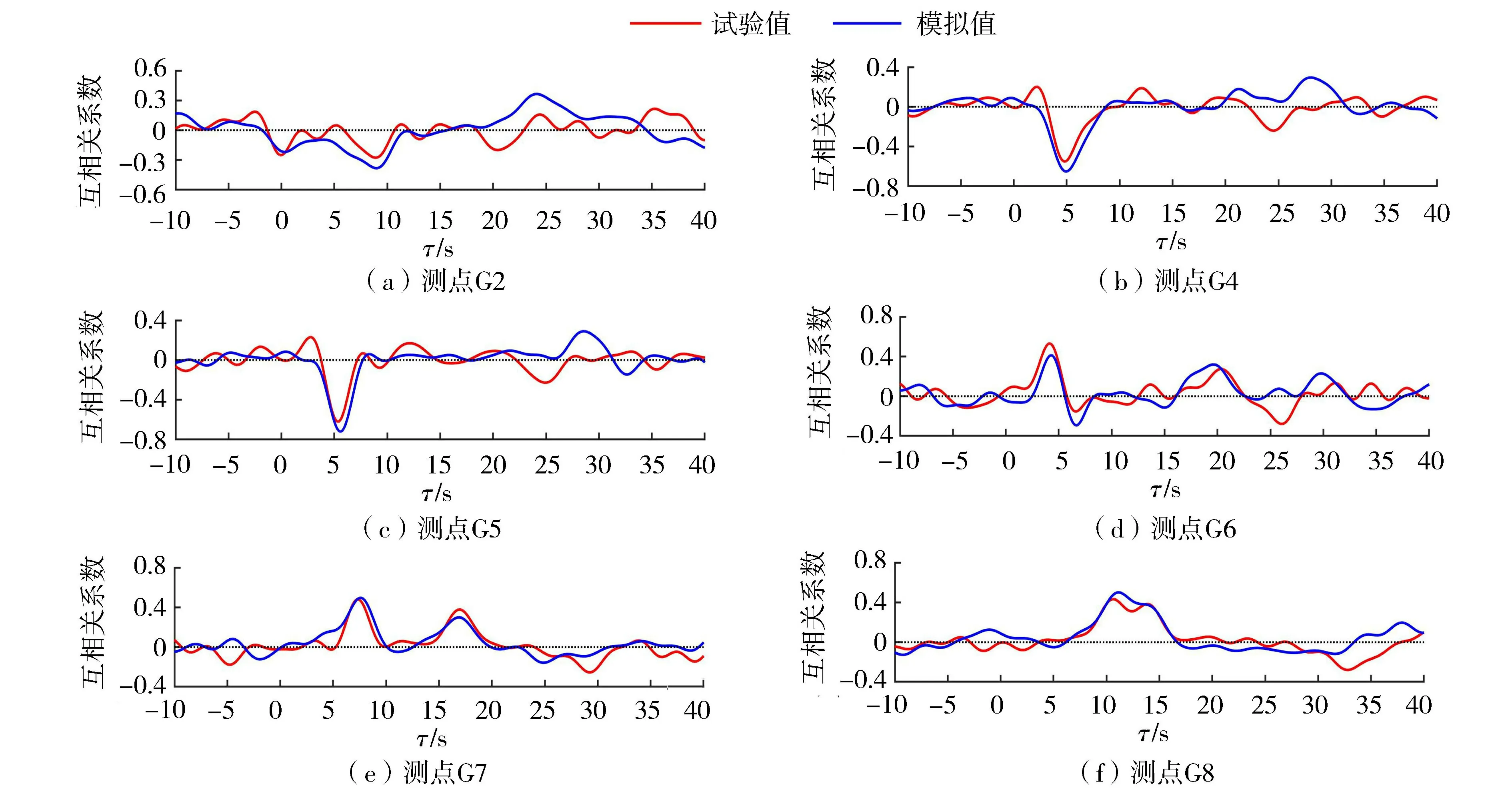
图5 测点G2处短波包络与各测点次重力波互相关分析Fig.5 Cross-correlation analysis between short-wave envelopes at G2 and IG wave motions at gauges

3.2 波能的沿程变化

波浪在岸礁地形传播过程中伴随着波能在低频与高频间的传递，该过程与次重力波关系密切。图6(a)～(d)为波能谱的试验值与模拟值对比，选取的4个测点分别代表了礁前常水深处、礁前斜坡、礁坪中部以及礁坪末端的频谱结构，黑色虚线用于区分次重力波与短波频段。测点G2模拟值与试验值在谱峰频段吻合较好，模型对低频段频率f≈0.03 Hz处的谱峰的高估导致此处次重力波有效波高模拟值较试验值偏大；测点G5由于水深减小，谱峰频率两侧的低频与高频波能均有所增长；波浪到达测点G7、G8时短波能量已大量耗散，模型较准确地捕捉了礁坪上几个主要的低频谱峰，测点G8在0.03 Hz附近的显著谱峰与礁坪上理论一阶共振放大频率较吻合[9]。结合互相关分析结果和测点G2、G8在0.03 Hz附近显著的谱峰来看，造成测点G2该频率谱峰偏大的原因可能与模型礁后斜坡反射的次重力波以及边界二次反射的次重力波形成的驻波有关，测点G2正好位于该频率驻波波腹附近，而物理模型中由于长波的相位差异，测点G2在0.03 Hz附近波能并不显著。图6(e)～(h)为Test45与Test58在测点G2与G8的波能谱，试验值与模拟值均吻合较好，但两组工况同样存在礁前0.03 Hz附近波能高估的现象。

图6 波能谱试验值与模拟值对比Fig.6 Comparison of measured and predicted wave energy spectra

为了进一步研究波能在高频与低频间的传递过程，考虑到次重力波周期较长，采用Dong等[21]Morlet小波二阶谱理论对波浪间的非线性相互作用进行分析，该方法相比基于傅里叶变换的二阶谱法在相同条件下可达到更高的显著性水平。对满足f1+f2=f3频率关系的波浪信号小波二阶谱Bw表达式为

(10)

式中：WT(f,t)——波面时间序列小波变换结果；上标*表示复共轭。该二阶谱表示时间T内频率为f1和f2的波浪与频率为f3的波浪间的相互作用程度，其中虚部代表能量的传递，虚部为正，能量由(f1，f2)传递至f3，如果为负则能量传递方向相反，虚部为0则波浪处于稳定状态,该频率之间无波能传递。图7为Test48测点G2、G5、G8的试验值与模拟值小波二阶谱虚部图。

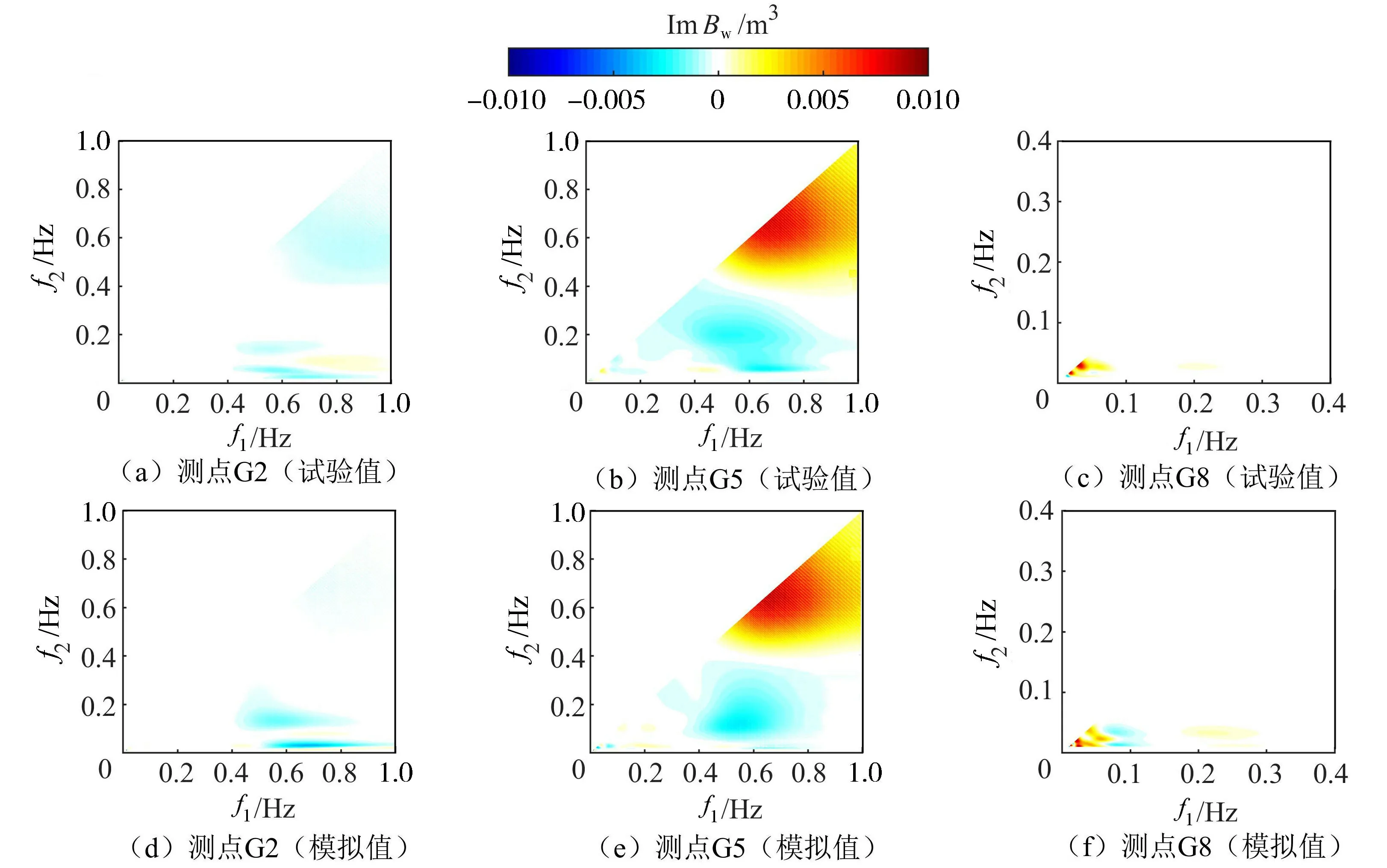
图7 试验值与模拟值的小波二阶谱虚部Fig.7 Imaginary part of measured and predicted wavelet bispectra

测点G2(图7(a)(d))波能传递主要发生在短波与频率小于0.2 Hz的次重力波之间，能量由谱峰频段向低频段传播，模拟值对于该处的非线性作用强度较试验值偏大，但对于高频段传至谱峰频段处的能量有所低估，同时试验结果显示(0.1 Hz, 0.7 Hz)～(0.1 Hz, 0.9 Hz)存在能量向高频段的传递。试验值与模拟值都观察到0.03 Hz的长波从高频段得到能量，结合前文分析结果，除短波与约束波外，该处的能量传递可能还来自短波与二次反射的向岸长波之间。

测点G5(图7(b)(e))处存在较强的非线性相互作用，大量能量由谱峰频段传递至高频段，因此测点G5波能谱在2倍谱峰频率处有较显著谱峰，该过程中超谐波生成。同时0.05～0.35 Hz频段附近的低频波从高频段获得能量，造成约束波幅值增长。

测点G8(图7(c)(f))显示礁坪末端的非线性能量传递主要发生于次重力波之间，原因是短波受波浪破碎与礁坪底摩阻作用已大量耗散，到达礁坪末端的短波波能很小，虽然模型对于某些低频处非线性能量传递的模拟值与试验值略有差异，但总体趋势基本一致。