计算单元边长对分布式流域水文模型模拟结果的影响
2021-09-13孔祥意刘志雨周国良李致家
孔祥意,刘志雨,,周国良,李致家
(1.水利部信息中心(水利部水文水资源监测预报中心),北京 100053; 2.河海大学水文水资源学院,江苏 南京 210098)
流域内的水文过程具有四维性,即三维空间和时间属性,具有物理基础的分布式流域水文模型[1]正是为描述水文过程的四维性而提出的。该类模型的根本特点为模型的输入(包括参数、初始条件、边界条件等)和输出均具有空间分布性[2-3]。目前,具有物理基础的分布式流域水文模型大都以DEM栅格作为模型的计算单元[4-5]。该类模型认为,在每一个计算单元网格内的气象、下垫面及地形特征分布均匀[6]。
计算单元网格越小,越能表征流域的地形地貌特征,保留更多的流域地形地貌信息,真实体现流域的水文响应特性。但在流域面积一定的情况下,采用小尺度网格离散流域会使计算单元网格数量急剧增加,随之而来的是繁重的计算量,影响分布式流域水文模型在实际应用中参数的率定和实时计算的时效性。因此,在较大流域中,大都采用较低分辨率DEM(如1 000 m ×1 000 m)构建具有物理基础的分布式流域水文模型[7-8]。
目前普遍认为,具有物理基础的分布式流域水文模型的最显著优势是:其中的参数可以根据下垫面条件及相关文献资料(如公开出版发行的手册等,下同)中提供的参数值与下垫面条件对照关系直接获得,不需要利用实测水文资料率定,使得该类模型可以用于无资料流域。在有资料流域的应用结果表明,绝大多数情况下直接采用文献资料中的参数,尤其是糙率(流速参数),模型的模拟效果不好。要想得到理想的模拟结果,必须重新率定,且不同大小计算单元的模型率定后其糙率值差别明显[9-10]。分析认为,文献中列出的参数与下垫面条件的对应关系,是基于真实的地形特征获得的;而分布式水文模型采用DEM栅格为计算单元,对流域地表进行了离散处理,每一个栅格内的地形特征(如坡度)被均化,已非真实地表特征。计算单元大小不同,对地表特征均化程度不同。因此,在具有物理基础的分布式流域水文模型的实际应用过程中,必须对由采用栅格作为计算单元导致的均化作用进行矫正。
目前的矫正方法主要分为两类:第一类为依据网格尺度直接矫正流速(或水流传播时间)[11],第二类为矫正地表糙率或矫正地形坡度[12]。目前,在有实测资料流域采用各种优化方法由水文气象资料率定模型参数,其实就是基于提取的非真实地形坡度对地表糙率进行矫正。王晓燕等[13]建立了流域平均坡度与DEM分辨率间的相关关系,并得到线性回归方程,用以矫正地形坡度,但所用DEM栅格尺度小于100 m,研究结论是否适用于更低分辨率的DEM有待验证。
本文所用模型为TOKASIDE(topgraphic kinematic approximation and saturation-infiltration double excess grid-based distributed model)[14],是根据Todini 等[15-16]提出的利用非线性水库方法模拟水文过程的理论构建的基于地形、运动波方法以及蓄满超渗双产流机制的网格化分布式模型。该模型为具有物理基础的分布式流域水文模型,以DEM栅格为计算单元,采用非线性运动波方程模拟水流运动[17-18]。模型将每一个计算单元中的水文过程概化为4个结构上相似的非线性水库方程,分别描述浅层土壤与深层土壤中的排水以及坡地地表径流和河道径流。模型采用了饱和及超渗产流机制,在整个降雨过程中,随着土壤含水量与降雨强度的变化,超渗与蓄满产流机制可能在每一个计算单元网格内交替发生[16]。
本文基于TOKASIDE模型,从固定参数下计算单元边长对模拟结果的影响机理及不同计算单元边长模型间参数移用误差矫正方法两个方面进行研究。
1 研究区概况
以淮河流域息县水文站以上部分(简称淮河流域)为研究区,地形情况如图1所示。所用DEM数据来源于地理空间数据云(http://www.gscloud.cn)提供的ASTER GDEM数据,栅格分辨率为30 m×30 m,所用其他分辨率DEM均为由ARCGIS工具再采样生成得到。由30 m×30 m分辨率DEM提取的流域面积为10 050 km2。为研究需要进行了子流域划分,划分结果如图2所示,子流域1~8的面积分别为2 166 km2、1 934 km2、694 km2、604 km2、268 km2、791 km2、2 012 km2和1 579 km2。
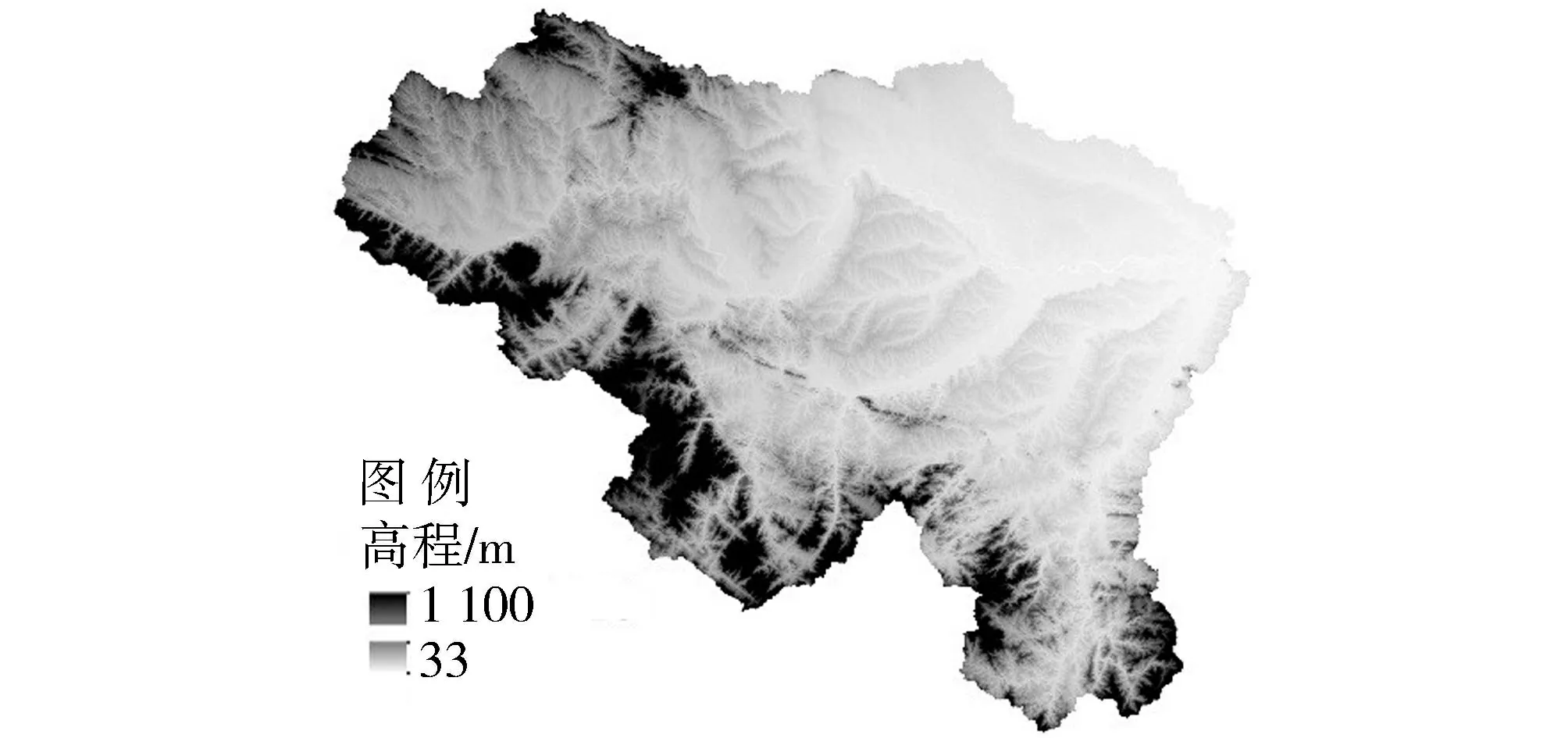
图1 淮河流域地形Fig.1 Topography of Huaihe River Basin
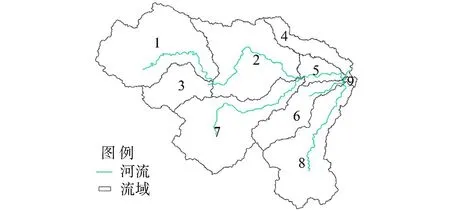
图2 子流域划分结果Fig.2 Sub watershed Division result
2 计算单元边长对TOKASIDE模拟结果的影响
2.1 对模拟径流过程的影响
由于研究流域面积较大,如果采用高分辨率DEM构建模型,则参数率定及洪水模拟的时间均会很长,因此采用基于2 000 m×2 000 m分辨率DEM的模型进行参数率定。另外又构建了基于300 m×300 m、500 m×500 m、800 m×800 m、1 000 m×1 000 m以及1 500 m×1 500 m分辨率DEM的5个模型,将率定的模型参数直接用于该5个模型,对201602号洪水的模拟结果如图3所示。由图3可以看出:(a)随着计算单元边长的减小,洪峰值逐渐增大,峰现时间逐渐提前;(b)洪峰值及峰现时间随单元尺度呈非均匀变化,分别在300 m和800 m处出现突变;(c)在某一单元尺度范围(如500~800 m,1 000~1 500 m),模拟结果相近。

图3 不同计算单元边长模型的模拟结果Fig.3 Simulation results of different cell scale models
2.2 对水量平衡要素的影响
选择模拟的流量过程退水段同时刻为结束点,基于不同计算单元边长模型模拟出的201602号洪水径流成分变化统计结果见表1。由表1可以看出:随着计算单元边长的增大,流域内的土壤含水量增量、地表水增量以及河道内水量(由于在模拟初期设定了15 m3/s的河道基流,表中负值代表洪水模拟结束后河道内总水量减少)呈增加趋势,而流出流域出口的径流量明显减少。这些变化均是由于坡地及河道内坡度或比降的减小所致。
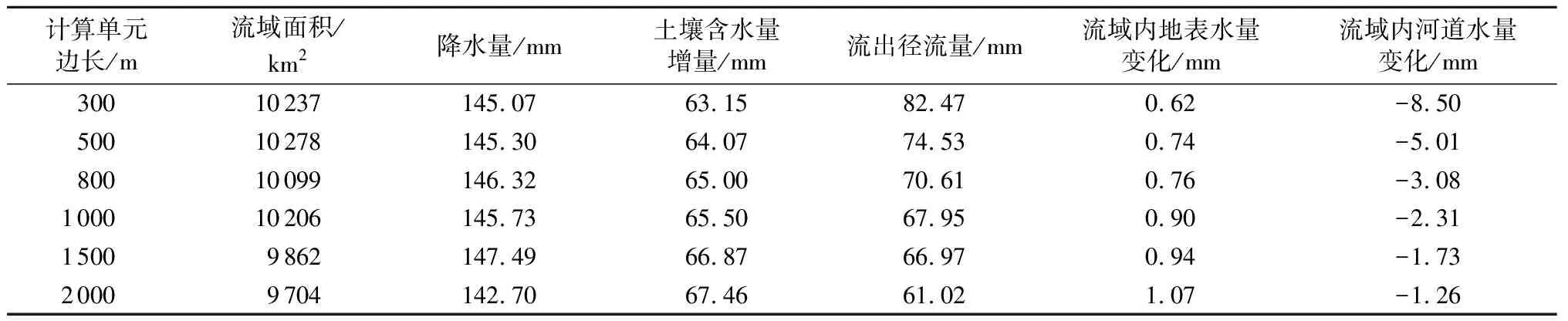
表1 201602号洪水径流成分统计
3 计算单元边长对模拟结果影响机理分析
3.1 对提取的流域坡度的影响机理
利用ARCGIS工具提取13个分辨率DEM对应的各子流域及全流域的平均坡度,如表2和图4所示。
由表2和图4可以看出:(a)山区性子流域,随着网格尺度的增大,平均坡度减小明显,且坡度减小的梯度逐渐减小;(b)处于平原内的子流域(如4号和 5号),DEM 栅格大小对坡度提取结果影响很小。
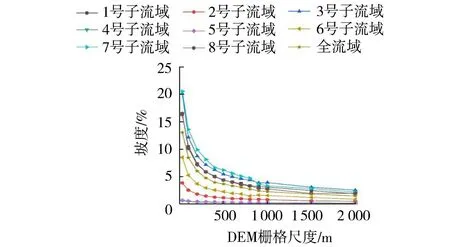
图4 流域坡度与DEM栅格尺度的关系Fig.4 Relationship between watershed slope and DEM grid scale
为了进一步研究流域坡度受 DEM 分辨率影响的变化规律,对表2进行归一化处理,即以 30 m×30 m 分辨率 DEM 对应的坡度为基数,用其他分辨率 DEM 对应的坡度与该基数之比,表示DEM分辨率降低后形成的流域坡度是30 m×30 m分辨率DEM对应坡度(认为是流域的真实坡度)的多少倍,即归一化处理后得到的结果为坡度变化与 DEM 栅格尺度之间的关系。归一化处理后的结果见表3和图5。

表2 由不同分辨率DEM提取的流域坡度
由表3和图5可以看出,归一化处理后不同子流域(含总流域)间坡度随DEM栅格尺度的变化规律高度相似,可以取平均线作为共同的变化趋势或变化规律,同时也说明不同流域间可以采用统一的表示方法,便于向无高分辨率DEM流域移用。从图5可见,提取的淮河流域平均坡度随DEM栅格尺度的增大呈非均匀减小时,在400 m和900 m处分别出现一次突变。

表3 不同分辨率DEM的流域坡度变化值
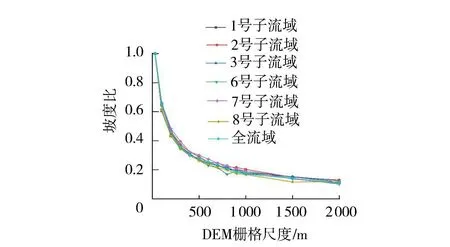
图5 流域坡度比与DEM栅格尺度的关系Fig.5 Relationship between watershed slope ratio and DEM grid scale
3.2 对提取的河段特征的影响机理
图6为由30 m×30 m分辨率DEM 提取的淮河流域水系(采用500 km2面积阈值),图7为4号、5号和8号3个河段河长度随DEM栅格尺度的变化。由图7可以看到河段长度整体呈现随栅格尺度增大而减小的变化趋势。分析认为,DEM分辨率对不同类型河段(内链和外链)的影响不同。对外链河段的影响主要表现在3个方面:(a)下游节点位置的变化;(b)由于分水线的变化,在同样集水面积阈值情况下,上游节点位置的变化(如8号子流域在DEM栅格边长大于800 m以后);(c)河段弯曲程度的变化。对内链河段的影响主要表现在两个方面:(a)上、下节点位置的变化;(b)河段弯曲程度的变化。
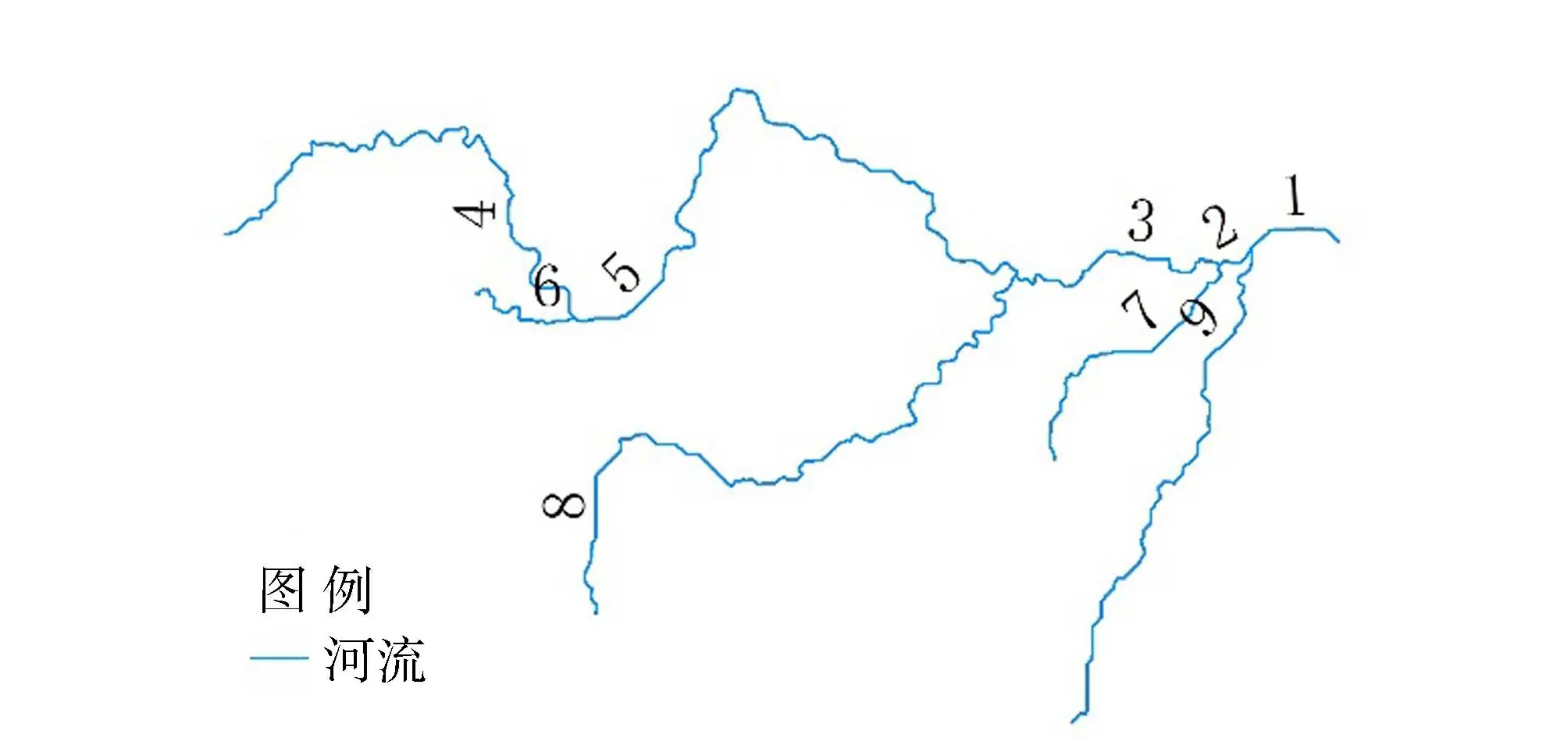
图6 河段及编码Fig.6 River reach and code
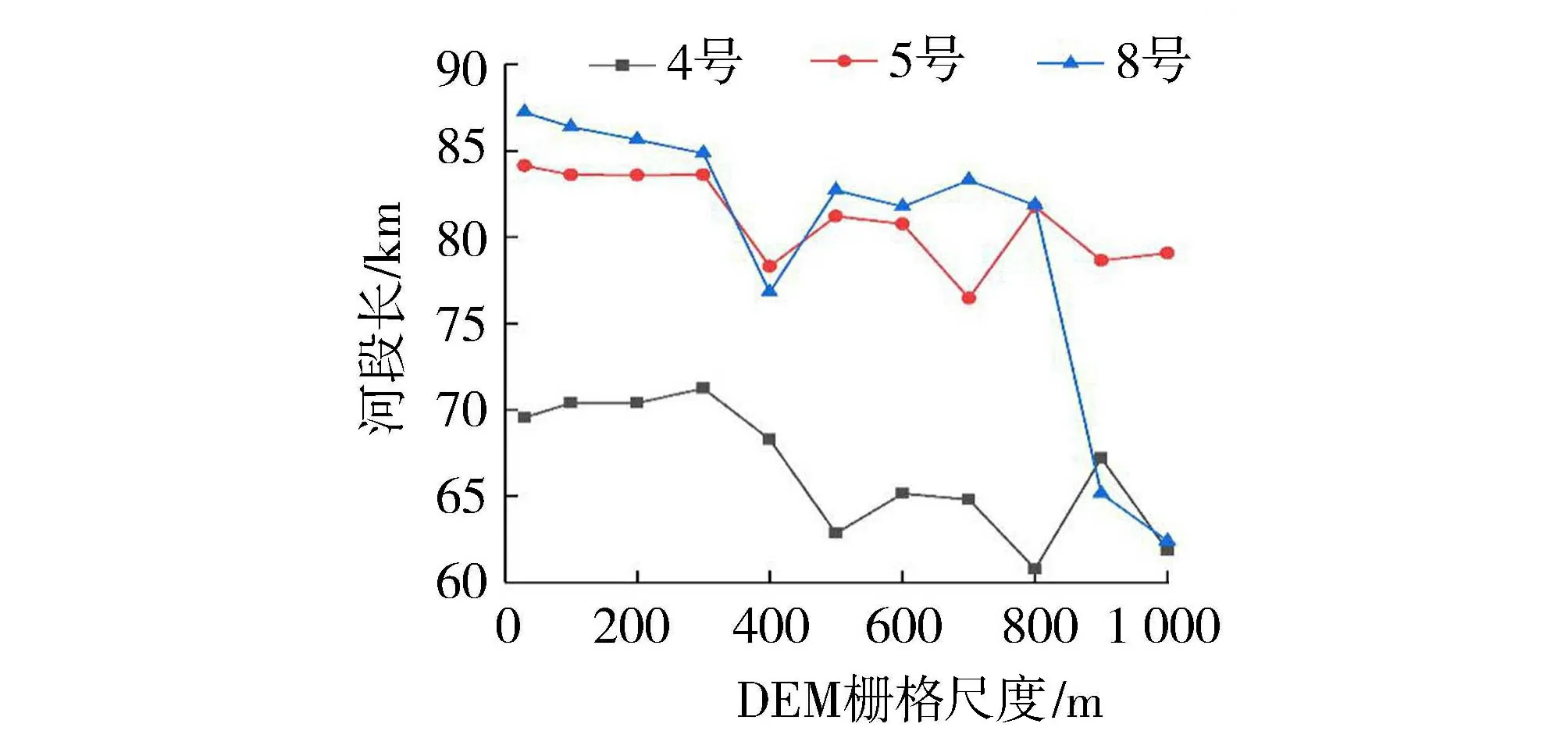
图7 河段长度随DEM栅格尺度的变化Fig.7 Variation of river reach scale with DEM grid scale
3.3 计算单元边长的影响分析
根据对提取的流域特征受DEM分辨率影响的分析可以看出,由于DEM栅格尺度的增大对地面点的高程具有均化作用,造成绝大部分栅格的坡度减小,进而减小了流域的平均坡度。尽管各子流域平均坡度可能相差很大,但平均坡度随着DEM栅格尺度的变化规律(相对变化)却非常一致。随着DEM栅格尺度的增大,流域坡度并非以均匀的梯度减小,最大减小梯度发生在200 m范围内。
栅格尺度的增大,改变了栅格的高程,从而改变了相邻网格间径流输入与输出关系,影响到每一个栅格内径流向流域出口汇集的路径,最终影响了整个流域的排水网络空间分布结构,表现为各河段的走势、长短的变化。DEM栅格尺度增大对排水网络的影响,主要表现在减小了河段长度,对比降影响不明显。
在其他条件完全相同的情况下,河段长度的减小,将缩短流域内各点向流域出口汇流的时间,导致模拟的洪峰出现时间提前,峰值增大。DEM栅格坡度及流域平均坡度的减小,又会增大流域各点的汇流时间,导致峰现时间推迟,峰值减小。可见,河段长度变化与坡度变化对径流过程的影响有相互抵消作用,可认为该抵消作用导致了图3中计算单元边长为500 m和800 m以及1 000 m和1 500 m的模拟结果相似。根据计算单元边长对模拟过程的影响结果(图3)可以看出,基于不同分辨率DEM模型的模拟结果之间之所以存在差异,主控因素为栅格坡度的不同(外部直接表现为提取的流域平均坡度的不同)。图3模拟的洪水过程分别在计算单元边长为300 ~500 m之间和800~1 000 m出现的突变与图5(b)中坡度随DEM栅格尺度变化的两个突变点完全吻合,证明了坡度对模拟结果影响的主控作用。
从模型结构及计算方法来看,计算单元坡度变化通过影响模型中计算的流速,进而影响单元间径流的转换强度,最终影响了流域出口的流量过程。
4 计算单元边长对模型影响的矫正方法
4.1 矫正方法
国内外广泛采用的坡面及河道流速计算公式中的下垫面糙率都是针对坡地与河道的真实坡度或比降(对应高分辨率DEM),因此,对于基于某一低分辨率DEM的模型,在直接采用提取的坡度或比降值计算坡面或河道内流速时,必须增加一个反映坡度影响的矫正因子,对非真实坡度或比降进行矫正,计算公式为
(1)
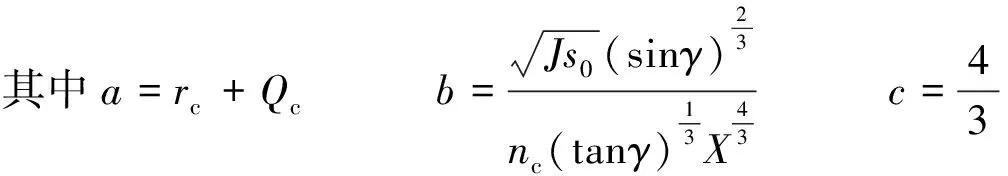
式中:Vc——计算单元内水体积;rc——计算单元内时段降水量;Qc——计算步长内计算单元的周边来水;s0——计算单元地表坡度;γ——边坡角度;nc——计算单元地表曼宁糙率系数;X——计算单元边长;J——坡度矫正系数,用以矫正因DEM空间分辨率变化引起的坡度提取误差,J的大小与流域平均坡度提取误差(用基于两个DEM提取的流域坡度的相对比值表示)有关。在实际应用时,必须有J与流域坡度比值间的关系曲线,该曲线需要由实测水文气象资料的流域分析得到。分析过程为:首先率定基于不同分辨率DEM的水文模型的J,然后由DEM分辨率根据归一化的流域坡度与DEM栅格尺度间的关系线得到流域坡度比,最后得到J值与流域坡度比之间的关系曲线。
可以看出,使用提出的矫正方法时需要两条关系曲线,第一条曲线是归一化的流域坡度与DEM栅格尺度间的关系线,第二条曲线是矫正系数与流域坡度比之间的关系线。
4.2 实例验证
将由计算单元边长为2 000 m模型率定的参数经过矫正后用于计算单元边长为400 m模型,以检验本文提出的矫正方法的有效性。采用4场洪水过程来分析J与流域坡度比值间的关系。由于率定参数时使用的是计算单元边长为2 000 m的模型,所以分析出的是相对单元尺度为2 000 m模型的矫正系数。计算结果如表4和图8所示。由表4和图8可以看出,不同大小计算单元的模型之间的矫正系数差别明显。
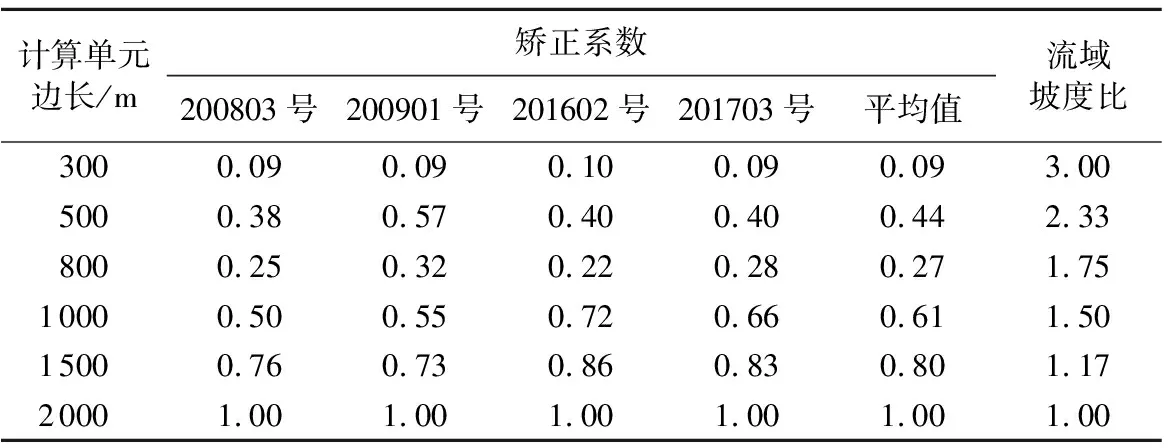
表4 矫正系数与计算单元边长及流域坡度比值关系

图8 2 000 m基准流域坡度比与 矫正系数关系Fig.8 Relationship between slope ratio and correction coefficient in 2000 m watershed
由图5可得400 m分辨率与30 m分辨率的平均坡度间的比值为0.30,2 000 m分辨率与30 m分辨率的平均坡度间的比值为0.11,则400 m分辨率与2 000 m分辨率的平均坡度间的比值为2.7。根据图8可得计算单元边长为400 m的模型对于计算单元边长为2 000 m模型的坡度矫正系数为0.222。
将由计算单元边长为2 000 m的模型率定所得参数以及矫正系数0.222用于计算单元边长为400 m的模型,模拟结果如图9所示。由图9可以看出,矫正后的模拟结果无论是流量过程线、洪峰流量还是峰现时间,均更加接近实测值,显著改善了模型的模拟效果。
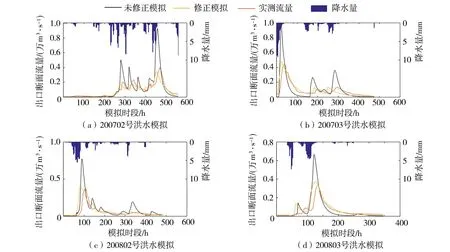
图9 矫正前后模拟洪水过程对比Fig.9 Comparison of simulated flood process before and after correction
4.3 矫正方法的使用
基于提出的矫正方法,在无资料大流域中可以按照以下步骤构建分布式流域水文模型:
a.目前较高分辨率DEM(如30 m×30 m)可以免费获得,更高分辨率的DEM也可以得到。借助GIS工具,经过再采样可以得到不同分辨率情况下的研究流域,进而得到归一化的流域坡度与DEM栅格尺度之间的关系曲线。
b.假定高分辨率DEM(如30 m×30 m或更小尺度)代表流域真实的地表特征,对应的分布式流域水文模型的糙率可直接取用相关文献中的数值。
c.借用有实测水文资料的流域,分析计算单元边长为30 m模型的矫正系数与坡度比值之间的关系曲线。
d.为减少计算量,增加模型运行的时效性,选择较低分辨率DEM构建分布式流域水文模型,根据模型计算单元边长确定矫正系数值,同时根据流域的下垫面条件从相关文献中查出对应的糙率及其他参数值,最后将矫正系数及参数值代入模型中,完成具有物理基础的分布式流域水文模型的构建。
5 结 语
本文研究了相同参数情况下计算单元边长对具有物理基础的分布式流域水文模型模拟结果的影响,根据DEM分辨率与提取的流域特征之间关系,分析了计算单元边长对模拟结果的影响机理。由于不同流域的真实地形坡度不同,使得随着DEM分辨率的变化,提取的流域坡度变化绝对值差异明显,但经过本文提出的归一化处理后,由DEM提取的流域坡度随DEM分辨率变化的相对值非常接近。可见,不同流域间流域坡度受DEM分辨率的影响具有极强的规律性。对于同一流域,相同地面糙率时分布式流域水文模型的模拟效果受计算单元边长大小的影响明显,主要是由计算单元对流域地形坡度均化作用的不同引起,且通常情况下不同计算单元边长的分布式流域水文模型之间糙率系数不宜直接移用。。
在对流域坡度与DEM分辨率关系研究的基础上,提出了可以消除计算单元边长对分布式流域水文模型影响的矫正方法,该方法可以在很大程度上消除由栅格均化作用导致的分布式流域水文模型的模拟误差,因此,能够有效地解决具有物理基础的分布式流域水文模型在无资料流域的应用问题。
