混凝土重力坝非黏滞阻尼地震响应分析
2021-09-13钱向东李震东
钱向东, 李震东, 李 晨
(河海大学力学与材料学院,江苏 南京 210098)
阻尼是描述结构振动过程中能量耗散的动力特性,是影响结构动力反应的重要因素之一,但由于其机理复杂,是人们了解得最少的结构动力学要素之一,不能像结构的质量、刚度等其他动力特性那样比较确切地表达。在工程结构动力分析中常将阻尼抽象为某种方便的数学模型,根据与结构反应物理量等效的原则确定其参数。
目前,在结构动力分析中最常用的阻尼模型为黏滞阻尼模型,该模型假定阻尼的大小与瞬时变形速度成正比,而方向与速度相反。黏滞阻尼模型由Rayleigh[1]首先提出,Rayleigh还进一步理想化地假设阻尼矩阵是质量矩阵和刚度矩阵的线性组合,因此这种阻尼模型还被称为“瑞利阻尼”“比例阻尼”或“经典阻尼”。基于黏滞阻尼模型的结构动力方程现已形成了一系列成熟的求解方法。在水工设计领域,混凝土重力坝的地震响应分析和抗震设计也是采用基于黏滞阻尼模型的动力学理论和方法。然而,从黏滞阻尼的机理分析,不难看出其振动一周的耗能与外干扰频率成正比,这与许多试验研究所观察到的结果不符合[2]。因此,基于黏滞阻尼模型的结构动力响应分析结果可能与结构的实际动力响应产生偏差,从而影响结构设计方案的安全性和合理性。
为了更好地描述结构振动的阻尼特性,人们提出了多种阻尼理论。这些理论基本上可以分为两类:一类是基于阻尼过程的物理机理,每一种理论对应着一种具体的阻尼现象;另一类注重数学处理上的方便,并不对应某一种具体的阻尼机理。结构地震反应分析中的阻尼所包含的耗能因素很多,机理相当复杂,难以采用具体的阻尼现象所对应的阻尼理论进行准确的解释和模拟。因此,在选取阻尼模型时依然倾向于数学处理上的方便,其中卷积型非黏滞阻尼模型因其在数学表达上相对简单,受到了研究者的关注[3-6]。该阻尼模型的阻尼力与速度的时间历程相关,在数学上表示为某一核函数与速度的卷积,可以更广泛地描述不同机制的阻尼作用,特别是阻尼作用的时滞效应。在卷积型非黏滞阻尼模型中,通过选择不同的核函数表达不同的阻尼模型,当核函数为狄拉克-δ函数时,该模型退化为黏滞阻尼模型。
混凝土材料具有黏弹性性质,弹性变形中的能量损耗与时间历史相关。本文尝试采用卷积型非黏滞阻尼模型分析混凝土重力坝的地震响应。选择指数函数为非黏滞阻尼的核函数,导出了非黏滞阻尼振动方程的状态空间表达式,以时域精细积分法求解地震作用下某重力坝响应时程,分析比较指数阻尼模型的松弛参数对坝体响应的影响。
1 非黏滞阻尼模型与振动方程
1.1 阻尼模型
在卷积型非黏滞阻尼模型中,指数阻尼模型是特别有前途的一种模型[6],尤其在黏弹性材料领域,该阻尼模型是建立在良好的物理基础之上的[7]。对于单自由度体系,阻尼力可以用卷积积分表示为
(1)
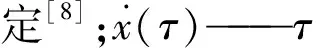
显然,当μ→∞时,核函数g(t)=μe-μt→δ(t)。此时,指数阻尼模型退化为黏滞阻尼模型:
(2)
关于混凝土材料松弛参数μ的取值,目前还很少有相关的试验资料,根据少量的针对钢筋混凝土梁的试验和阻尼参数设计的研究成果[9-11],μ的取值在130 s-1左右。
1.2 振动方程
重力坝地震响应分析一般采用有限单元法将问题简化为多自由度振动问题。对于多自由度体系,指数阻尼情况下的阻尼力向量可以表示为
(3)

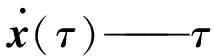
如果取n=1,则具有N个自由度体系的振动方程为
(4)
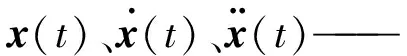
只考虑地震作用时
(5)
当采用无质量地基模型时,质量矩阵M具有零主元素,其逆矩阵不存在。设M的非零主元素个数为m,则引入m个线性无关向量rj∈RN(j=1,2,…,m),组成N×m阶矩阵:
r=(r1,r2,…,rm)
(6)
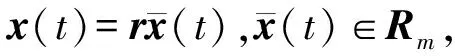
(7)
对式(7)两边同时前乘rT,则有
(8)
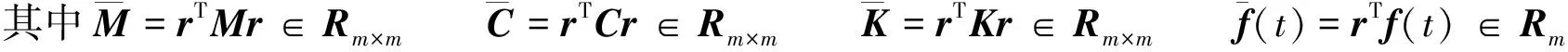
2 振动方程的精细积分算法
非黏滞阻尼多自由度体系振动方程(4)或(8)是一组耦合的二阶微分积分方程,常规的振型叠加法和数值积分法难以直接应用。通常采用引入辅助变量或状态变量,在状态空间中采用直接积分法和振型叠加法进行求解[12-13],前者得到的计算结果精度高,但计算量巨大,而后者虽计算速度较快,但精度较低。也有研究者对传统的数值积分法进行改进并应用于非黏滞阻尼振动方程的求解[14-17]。文献[18]引入状态空间并采用时域精细积分法求解了文献[13]的算例,计算效率明显提高。本文利用指数型非黏滞阻尼的特点,采用状态空间时域精细积分法求解振动方程(8)。
(9)
则方程(8)可以写为

(10)
对式(9)两边求导,可得

(11)
(12)
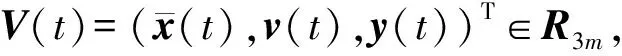
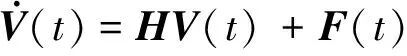
(13)
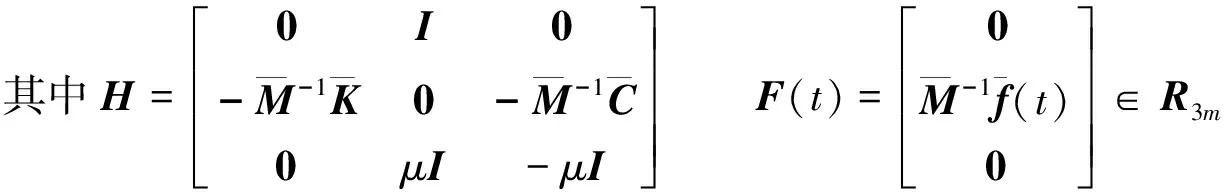
式中:I——m×m阶单位矩阵。
(14)
对时间按等间距Δt进行离散后,则t0、t1=t0+Δt、t2=t1+Δt、…、tk+1=tk+Δt,…各时刻的数值解可以采用精细积分法计算得到,此处不再赘述,可参见文献[19]。
3 算 例 分 析
以某重力坝的12号挡水坝段为例进行计算分析,重力坝体型和断面如图1所示。坝顶高程1 625.00 m,坝基面高程1 422.00 m,坝高203 m,坝顶宽16 m,正常蓄水位1 619 m。坝体采用平面应力单元,坝基采用平面应变单元。地基左右和底部边界施加法向约束。有限元网格如图2所示。
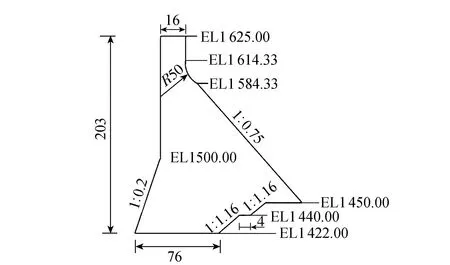
图1 重力坝体型及断面(单位:m)Fig.1 Body type and section of gravity dam (units: m)
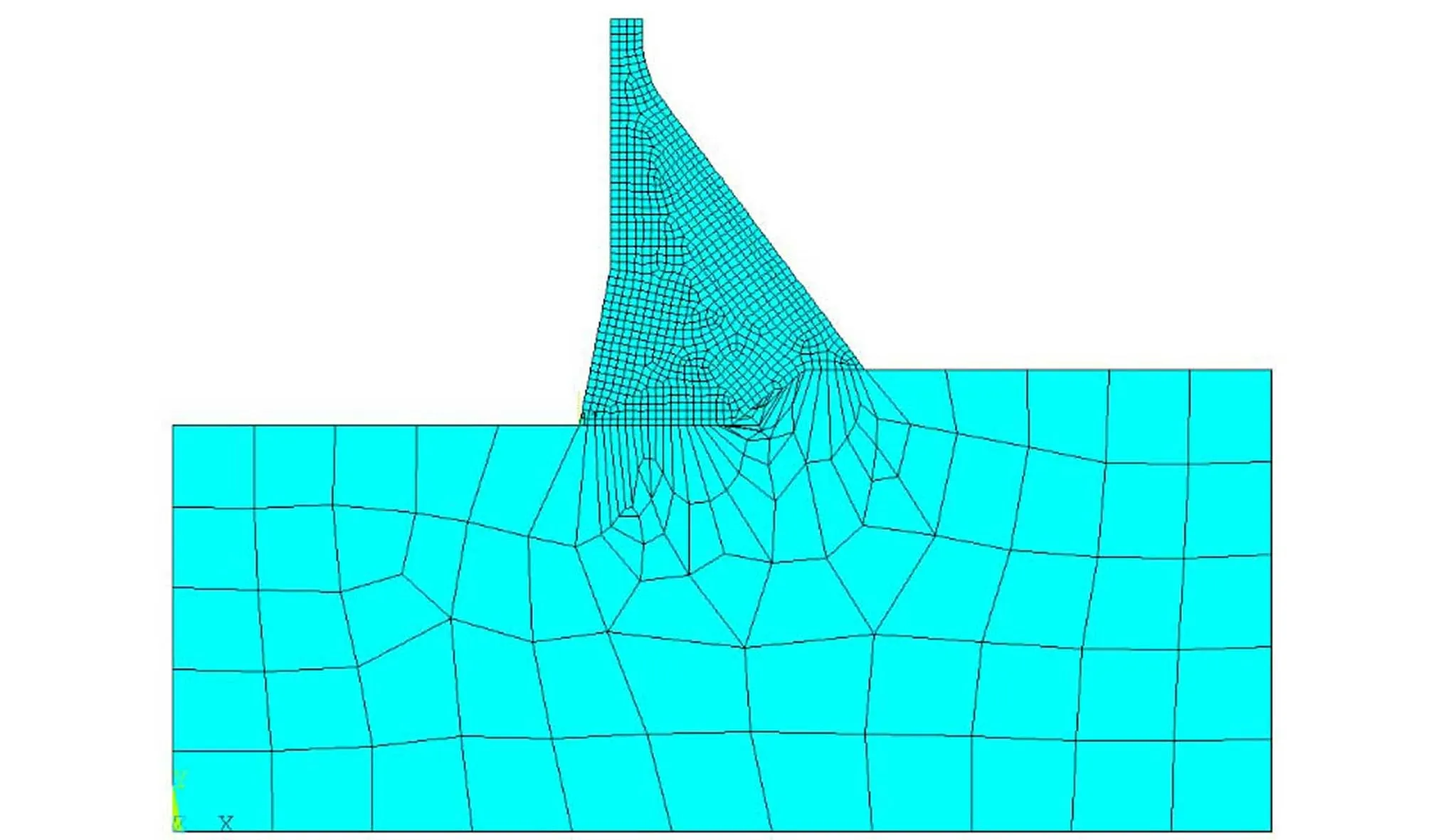
图2 有限元网格Fig.2 Finite element mesh
3.1 计算条件和参数
坝体混凝土静态弹性模量为25 GPa,容重为24 kN/m3,泊松比为0.167;地基岩体静态弹性模量为15 GPa,容重为27 kN/m3,泊松比为0.24。动弹性模量取静弹性模量的1.5倍,振型阻尼比统一取为5%。动力计算时采用无质量地基。计算时分别考虑空库和满库2种情况,其中满库时动水压力附加质量采用Westergaard公式计算。
黏滞阻尼模型计算时采用Rayleigh阻尼,阻尼系数矩阵C=αM+βK,α、β由系统的振型阻尼比和前两阶自振频率确定。非黏滞阻尼模型计算时,为了便于比较,采用与黏滞阻尼相同的阻尼系数矩阵C,而松弛参数μ的取值由于缺乏相关的试验资料,作为对比研究,分别取μ=60 s-1、100 s-1、130 s-1和200 s-1进行计算。精细积分时采用的时间间隔Δt=0.01 s,指数矩阵高精度计算采用220类算法。
地震动输入采用Koyna地震实测的加速度记录,水平向峰值加速度为4.647 8 m/s2、竖向峰值加速度为3.056 4 m/s2,如图 3所示。初始条件为t0=0,V(t0)=V0=0。
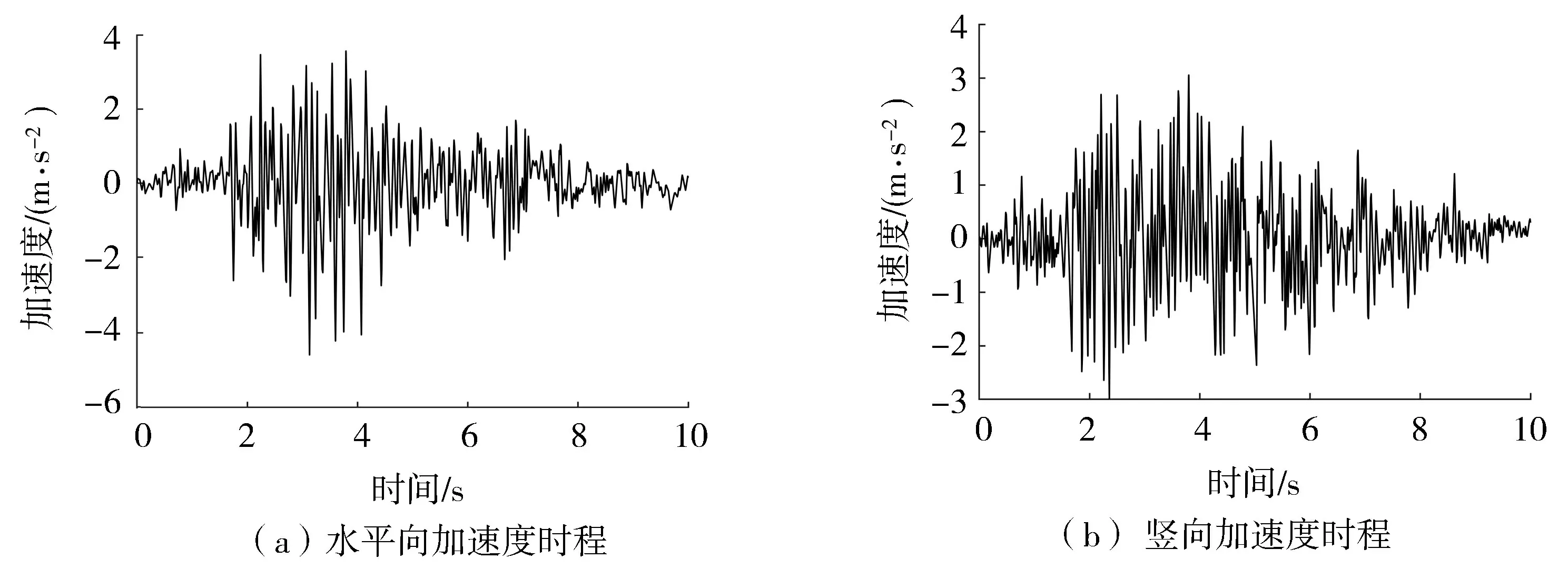
图3 Koyna地震波Fig.3 Koyna seismic wave
3.2 计算结果
为了验证有限元模型的正确性和合理性,首先分别计算了空库和满库情况下大坝的前5阶自振特性;然后采用状态空间精细积分法,分别计算了空库和满库情况下大坝在Koyna地震波作用下的位移、速度和加速度时程。
3.2.1 大坝自振特性
假定材料处于线弹性状态,采用Ansys计算得到大坝的前5阶自振频率如表1所示。
3.2.2 空库情况下坝体地震响应
实际计算时,先取μ=300 s-1进行试算,发现所得结果与黏滞阻尼的计算结果几乎一样。也验证了当μ取值很大时指数非黏滞阻尼模型退化为黏滞阻尼模型。由图4可以看出2组曲线基本重叠,说明就本算例而言μ=200 s-1时,指数非黏滞阻尼模型已接近黏滞阻尼模型。

图4 空库情况下坝顶水平向位移和加速度时程Fig.4 Time histories of displacement and acceleration at dam crest with empty reservoir
图5给出了空库情况下μ取不同值数值时坝顶水平向位移和加速度的时程曲线,表2为空库各种阻尼情况下坝体水平向位移、速度和加速度的响应峰值。
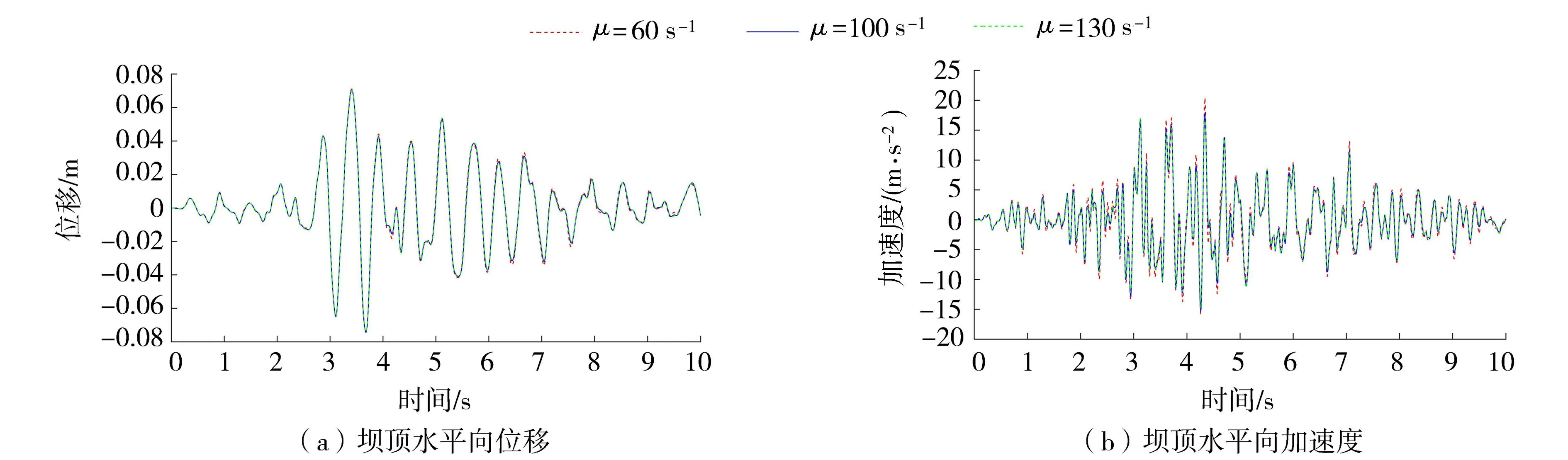
图5 空库情况下松弛参数对坝体响应的影响Fig.5 Influence of relaxation parameter on dam responses with empty reservoir
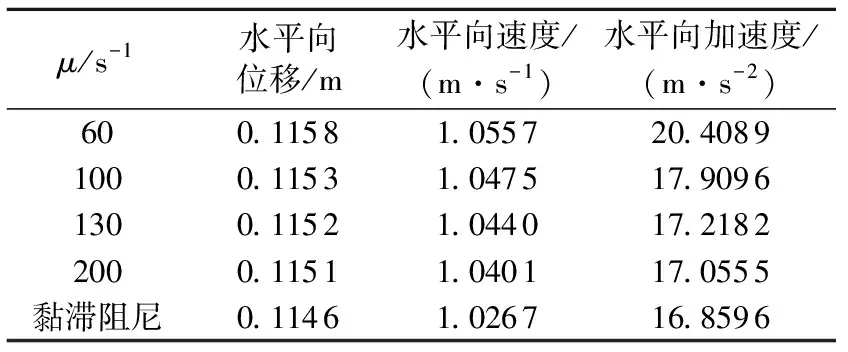
表2 空库情况下坝体响应峰值
3.2.3 满库情况下坝体地震响应
图6给出了满库情况下μ取不同值数值时坝顶水平向位移和加速度的时程曲线,表3为满库各种阻尼情况下坝体水平向位移、速度和加速度的响应峰值。
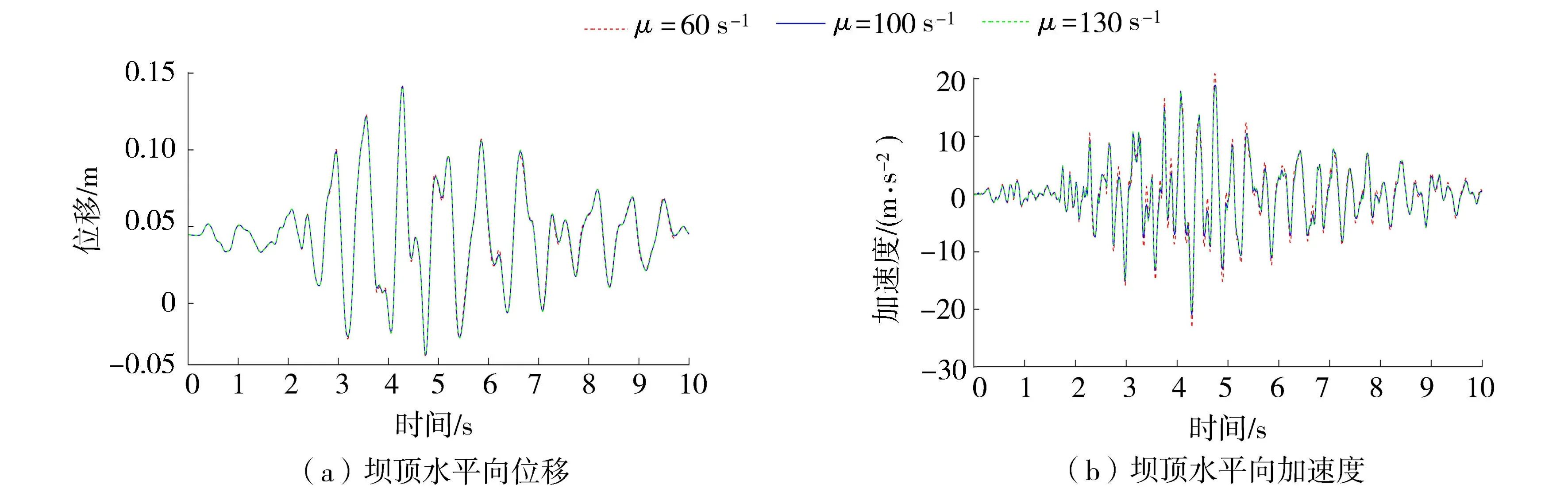
图6 满库情况下松弛参数对坝体响应的影响Fig.6 Influence of relaxation parameter on dam responses with full reservoir
3.3 结果分析与讨论
由图5和图6可知,无论是空库还是满库,非黏滞阻尼模型对加速度响应的影响明显大于对位移响应的影响。从表2和表3也可以看出非黏滞阻尼模型对加速度峰值响应影响最大,其次是速度峰值响应,对位移峰值响应的影响最小。无论是空库还是满库,非黏滞阻尼模型的峰值响应均大于黏滞阻尼模型的峰值响应。随着μ的减小,非黏滞阻尼模型的峰值响应增大,说明黏滞阻尼模型的阻尼效应大于非黏滞阻尼模型。因此,采用黏滞阻尼模型分析工程结构的动力响应时,可能会低估响应的峰值。
表4为μ取不同数值时非黏滞阻尼模型得到的坝体响应峰值相对于黏滞阻尼模型坝体响应峰值的增幅。空库情况下,当μ<100 s-1时,非黏滞阻尼模型的水平向加速度峰值增幅超过5%。而满库情况下,当μ<100 s-1时,非黏滞阻尼模型的水平向加速度峰值增幅超过10%。特别地,当μ<60 s-1时,水平向加速度峰值增幅超过20%。
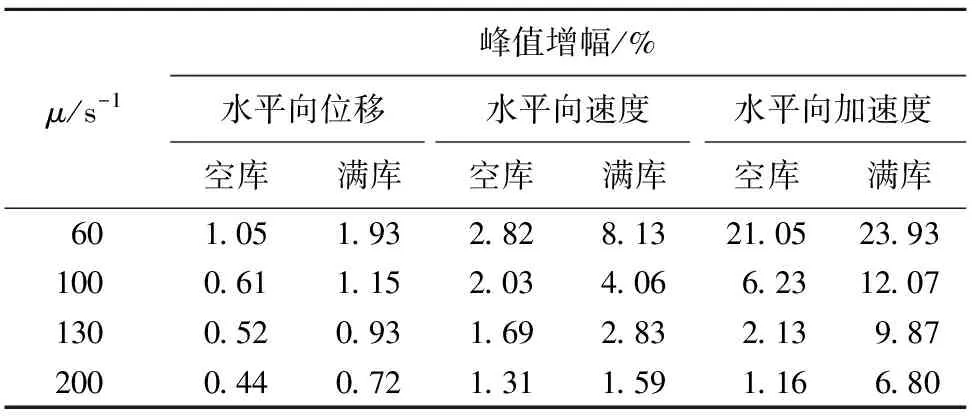
表4 非黏滞阻尼模型相对于黏滞阻尼 模型坝体响应峰值的增幅
4 结 论
a.采用状态空间时域精细积分法求解指数卷积型非黏滞阻尼结构振动方程,可以避免各时刻的卷积积分及其误差引起的数值不稳定,也不需要额外的矩阵求逆运算,可应用于大型系统的非黏滞阻尼振动方程的求解。
b.本文算例表明,地震作用下非黏滞阻尼模型的峰值响应均大于黏滞阻尼模型的峰值响应。随着μ取值的减小,即与黏滞阻尼模型的差别增大,非黏滞阻尼模型的峰值响应就越大,说明黏滞阻尼模型的阻尼效应大于非黏滞阻尼模型。因此,采用黏滞阻尼模型分析工程结构的动力响应时,可能会低估响应的峰值。
c.本文算例表明,地震作用下非黏滞阻尼模型对结构位移、速度和加速度响应的影响程度不尽相同,影响最大的是加速度响应,位移响应影响相对较小。
d.由于缺乏试验资料,本文对混凝土松弛参数的取值可能不一定符合实际情况,因此本文的研究只是对非黏滞阻尼模型在混凝土大坝地震响应分析中的应用做一个尝试,后续的研究应开展混凝土材料非黏滞阻尼特性的试验和参数识别,正确认识和建立合理的混凝土材料阻尼模型,以便更加科学有效地开展混凝土结构的地震响应分析和抗震设计。
