课程思政元素融入高职高等数学的教学探讨

应希源 萨彬含

[摘           要]  以高职院校高等数学曲线上一点处的切线定义教学为例，引入嫦娥五号探月工程视频片段创设问题情境，增强学生的民族自豪感和文化自信感。通过返回器的半弹道跳跃式再入返回方式，让学生了解科学家精益求精、科学严谨的态度。通过研究轨道曲线一点处的切线，激发学生发扬先辈们勇于探索、不断创新的精神。

[关    键   词]  高职;课程思政;高等数学;探讨

[中图分类号]  G712                   [文献标志码]  A                      [文章编号]  2096-0603（2021）32-0090-02

一、引言

切线问题是导致微积分诞生的最重要问题之一，切线斜率作为导数概念的引例，已出现在今天的任何一本微积分教材中[1]，但曲线上一点处切线的定义往往在教材中直接给出，部分高职学生因缺乏对该定义历史背景的了解，对理解该定义存在一定的困难，从而在学习导数概念前就产生畏难情绪。应用课堂教学，引入课程思政元素，让高职学生了解曲线上一点处切线定义的演变，认识该定义背后的历程及艰辛，对提高高职学生学习兴趣、消除畏难情、培养坚强的毅力具有重要的意义。

学者任卫兵[2]以曲线上一点处的切线为例，从数学史视角出发，提出了基于HPM视角的概念、教学实践与思考。学者邓迎春[3]用发生教学法设计和实施“曲线上一点处的切线”的教学。本文在此基础上，针对高职学生，以嫦娥五号返回器的一段轨迹为例，引入课程思政元素，对曲线一点处的切线定义进行教学探讨。

二、教学设计思路

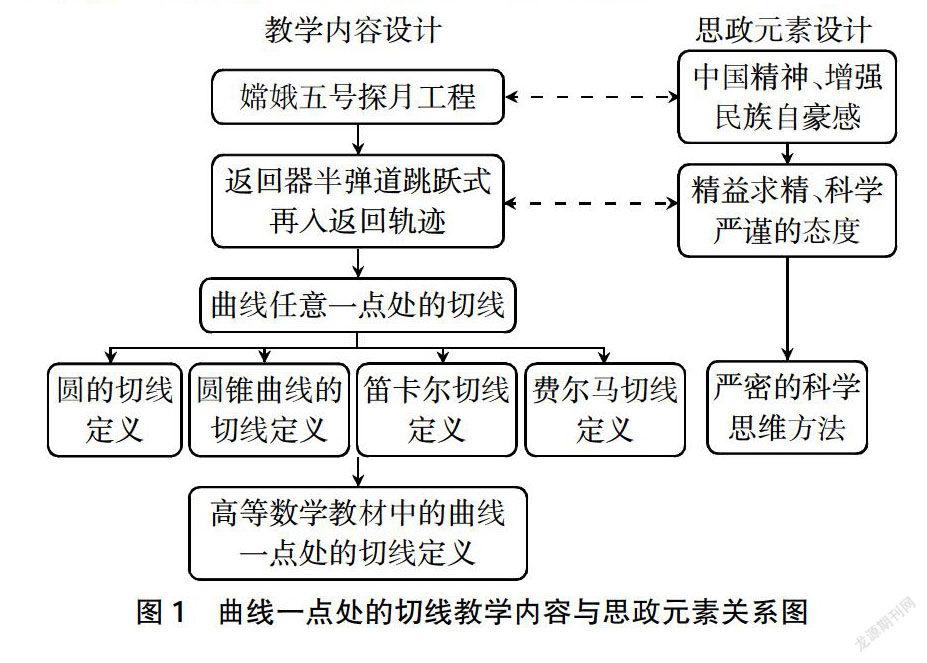
本節课将课程思政元素融入教学中，以“创设情境—提出问题—分析问题—解决问题”为主线，进行曲线上一点处的切线定义的教学探讨。通过嫦娥五号探月升空视频片段，介绍嫦娥五号取得的举世瞩目的成就，并从返回器“打水漂”的半弹道跳跃式再入返回轨迹提出问题，探讨曲线上一点处切线的定义。教学内容和思政元素的联系和逻辑关系如图1所示。

三、教学过程

（一）创设情境，提出问题

以嫦娥五号发射的视频片段作为引例，简要介绍嫦娥五号发射的意义，嫦娥五号返回器采用“打水漂”的半弹道跳跃式再入返回方式安全着陆，划出了优美的曲线，返回器着陆前的一段轨迹如图2所示的曲线。基于此背景设计问题：如何描述轨迹上一点处返回器的运动方向？学生思考后，根据已有的知识，回答可由轨道上该点处的切线方向来确定。接着追问：那如何确定轨道上一点处的切线呢？

（二）分析、解决问题

如何确定曲线上一点处的切线？部分学生利用已有圆的切线定义可得出，在曲线上一点处直线与曲线只有一个公共交点，则该直线为曲线在该点处的切线。教师引导学生举出反例如图2（a）所示，曲线在A点处，直线与曲线均只有一个交点，但不是曲线在该点处的切线。因此，圆的切线定义不能直接应用于任意的曲线。

教师再引导学生回顾高中所学的圆锥曲线的切线定义：圆锥曲线的切线与圆锥曲线只有一个公共点，且全部在圆锥曲线之外的直线。该定义是否适用于任意曲线呢？学生思考后可举出反例如图2（b）所示，直线是曲线在B点处的切线，但该切线与曲线有两个交点，且不在曲线之外，因此，不能将圆锥曲线的切线定义直接应用于本问题提出的曲线，那曲线任意点处的切线又该如何定义呢？

因高职高等数学教材省略了切线概念的历史背景，直接给出了曲线切线的定义，学生难以理解，因此，教师引导学生简要回顾曲线一点处切线定义的历史演变[4-5]，从圆锥曲线切线定义到高等数学教材曲线一点处切线的定义，经历了约2000年的演变，其中较为典型的有阿基米德切线定义、笛卡尔“等根法”求切线、费尔马“极值法”求切线、巴罗的“特征三角形法”求切线、牛顿的“流数法”和莱布尼兹的“坐标差分法”求切线、达兰贝尔切线定义等。其中阿基米德将螺旋线的切线看作与螺旋线只有一个公共点，且落在螺旋线之外的直线，仍从公共点的个数角度来研究切线。直到17世纪，笛卡尔、费尔马、巴罗等才给出求曲线切线的一般方法。牛顿的“流数法”和莱布尼兹的“坐标差分法”是在没有建立极限理论的基础上提出的，在欧洲大陆流传了半个多世纪。随着极限理论的逐步发展，达兰贝尔给出了曲线一点处切线的定义：割线与曲线的两个交点变成一个点时割线的极限，但该定义仍然没有把“两点变成一点”这一过程形象化描述出来。

随着极限理论的逐步完善，约在19世纪才产生了现在高等数学教材上的定义，目前高等数学教材中曲线一点处切线的定义为：设有曲线C及C上的一点M，在点M外另取C上一点N，作割线MN，当点N沿曲线C趋于点M时，如果割线MN绕点M旋转而趋于极限位置MT，直线MT就称为曲线C在点M处的切线，这里极限位置的含义是：只要弦长|MN|趋于0，∠NMT也趋于0[6]，根据该定义，如果当点N沿曲线C趋于点M时，如果极限k=存在，则该极限就是切线MT的斜率。

学生了解曲线一点处切线定义的历史演变后，根据高等数学教材所给的定义，便可做出嫦娥五号返回器着陆前的一段轨迹曲线上点M的切线，如图3所示，直线MT即为曲线在点M处的切线。

（三）定义的应用及探讨

例1.如何根据定义找出曲线在M点处的切线？

部分学生根据“切线是割线的极限位置”很难理解具体哪条直线才是割线的具体位置。如当N点沿着曲线跨过M点过程中，当M点与N点完全重合时，直线与曲线只有一个交点，而过一点的直线有无数条，究竟哪一条才是曲线在M点处的切线呢？此时可引导学生紧扣定义，学生可根据定义中的当弦长|MN|趋于0时，∠NMT也趋于0，则可判断MT就是所求的切线，求出极限k=，便可得到点M处切线的具体位置。