半线性椭圆方程多解问题的改进牛顿流线法
2021-09-11李夏云
李夏云 肖 喜 罗 园 黄 晞
(湖南城市学院 理学院,湖南 益阳 413000)
1 概论
由于新的先进技术的发展,许多研究人员对为新的应用寻找非线性问题的多解很感兴趣,并致力于开发新数值方法[1-8]来寻找其多解。本文考虑寻找下面半线性椭圆方程的多个解

Ω 是RN上的有界区域,假设非线性项f(x,u)在Ω×R 上满足局部Lipschitz 连续,其相应的能量泛函为


目标方程组(3)是非线性方程组,对于其解法文[7-8]从牛顿场的观点出发提出了沿场线的追踪算法——牛顿场线法。
2 改进的牛顿流线法数学结构及算法
2.1 牛顿流线法的数学结构

定理3[7]:设F(x)在闭子域G∈Ω 中是V- 正则的,若在边界上每一点x0的牛顿方向V(x0)指向Ω 的内部,则在Ω 中必存在根x*。
从上面分析来看:牛顿流线法允许从任何不在根附近的初值开始计算,在有根的区域中,总流量||F(x(t))||是沿着流线方向向根汇聚的,形成一个中心场,则以其中任意一点为起点,追踪中心场,可以求得此根;若在无根的区域,总流量||F(x(t))||是减小的,从一端通向另一端,且大范围按指数收敛。
2.2 牛顿流线法算法

2.3 牛顿流线法算法改进分析

其中B0=(A)-1,A0=DF(x0),sj=xj+1-xj。Broyden 方法与牛顿方法是一致的,在奇点附近,我们采用牛顿流算法,在根的附近,就采用Broyden 方法,其可以避免误差的积累传播,有较快的收敛速度,计算工作量从O(n3)降到O(n2)。
3 半线性椭圆方程多解的改进牛顿流线计算法举例


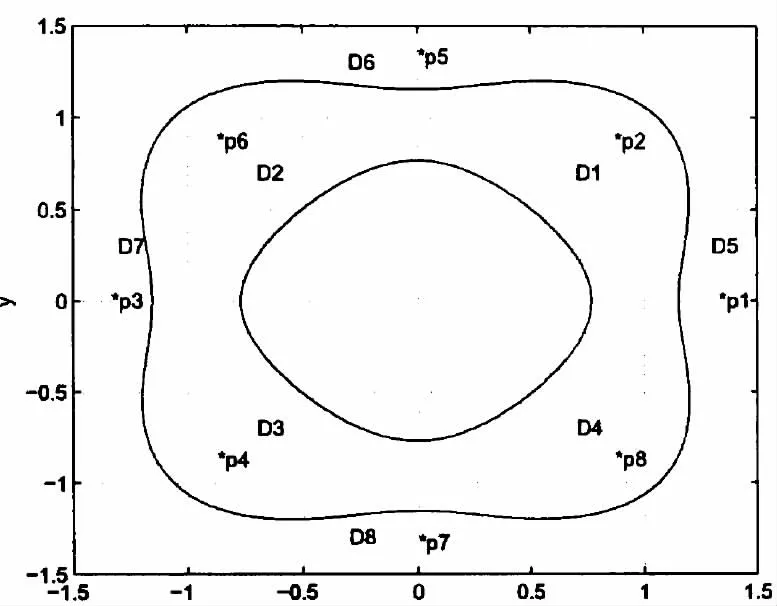
图1
有3 个三重特征值,取λ17=λ71=λ55=50,用主部u=aφ17+bφ71+cφ55,通过分析可以得到26 个非零根;
有 18 个 四 重 特 征 值 取 λ47=λ74=λ18=λ81=65,u=aφ47+bφ74+cφ18+dφ81,通过计算可以得到80 个非零根;
有1 个6 重特征值,5 重特征值(很少,在10000 内只搜素到两个),相应的多解计算很困难。若简单地增加许多基作延拓计算,而初值取的不好,则迭代将发散。按特征值的大小取:λ11=2,λ22=8,λ13=λ31=10,λ33=18,λ24=λ42=20,这7 个值中,有2 个二重值,3 个单值,按前面的搜索延拓法:应该可以得到22 个非零解。其近似解u7(x,y)的系数满足非线性方程组:

下面用改进的牛顿流线法来对其进行计算:在区域[-3,3]上随机取点,取n=35000,调用Matlab 中的rand 函数,得到一个8×35000 的随机矩阵,共35000 个初值,通过计算,得到84 个非零解,与前面的28 个解比较,多了56 个不同的新解,不同的特征值直接可以产生新的多解,例如新解为u1,u2,u3它们对应的初值分别为:

图2~图7 分别列出了初值与对应真解u1,u2,u3的图形,注意解和初值的图非常相似。
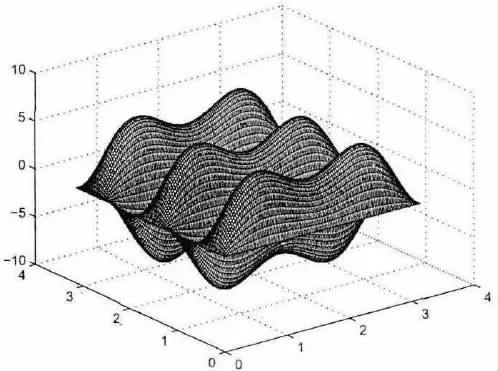
图2 初值u1 图像
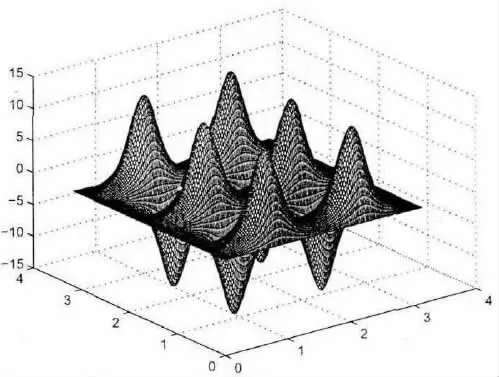
图3 真解u1 图像

图4 初值u2 图像
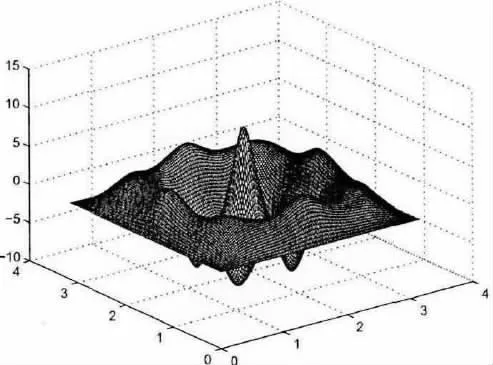
图5 真解u2 图像
图6 初值u3 图像
图7 真值u3 图像
4 结论
以上计算和分析表明,求解非线性方程的多解问题,经过牛顿流处理以后,在奇点附近,我们采用牛顿流算法,在根的附近,就采用Broyden 方法,效果与牛顿流线法差不多,迭代次数没有改变,但计算量可以明显减少,其可以避免误差的积累传播,有较快的收敛速度,计算工作量从O(n3)降到了O(n2)。从解的图形可以看到,和初值比,解的峰更高,腰更细。
上面方程组取8 个基,随机投入35000 个初始点,每个点迭代20 次,要计算4.48×107个积分,计算量比较大。此种算法可以采用并行计算,来提高解题的效率。
