圆柱形叶片单圆弧型线的绘形及分析*

陈 月，宋小娟，杨钧凯，王 桃

（西华大学能源与动力工程学院，四川 成都610039）

圆柱形叶片是低比转速离心泵叶轮的基本叶片形式。叶片的水力性能是由叶片的几何形态决定的，而叶片的几何形态又可以叶片轴面投影图和平面投影图两个图样表达。为提高圆柱形叶片的效率等性能指标，众多学者在改进圆柱形叶片的绘形方法方面展开了长期的研究，并取得了许多有价值的成果。文献[1]描述了叶轮流道的平面投影和轴面投影的绘图原则；文献[2]给出了准确的此类叶片的三维建模方法。圆柱形叶片表面的传统平面投影图有：单圆弧、多圆弧、等变角螺线、非等变角螺线、渐开线等等[3-9]。单圆弧曲线叶片具有结构简单、造型方便且沿曲线曲率半径无变化等优点，是一种在设计实践中最早使用且使用至今的叶片型线。为方便设计人员准确、快捷地绘形这种有优势的叶片投影，课题组将介绍两种单圆弧曲线的绘形新方法，并给出其包角的计算式。

1 圆柱形叶片投影概述

在设计实践中，应根据前期已计算确定的叶轮几何参数首先绘制叶片的轴面投影图，如图1所示。其中，b2、R2、R0应等于理论计算值。同时，应在轴面图上确定叶片进口边，还必须精确计算进口边和后盖板流线交点处的叶片安放角，以及这一角度在与叶轮轴心线垂直的平面上的投影角β1，并确定叶片进口边与前、后盖板流线相交处的半径R1A、R1B。叶片出口安放角在上述平面上的投影可认为近似不变，等于前期计算的β2。

图1 叶片轴面投影图Fig.1 Meridional section of blade

圆柱形叶片有一不同于扭曲叶片的重要特点：叶片工作面与前盖板内表面相交所得交线是一空间曲线；叶片工作面与后盖板内表面相交所得交线也是一空间曲线。上述两条空间曲线在与叶轮轴心线垂直平面上的投影是两条平面曲线，叶片工作面本身在这一平面的投影是第三条平面曲线，这三条平面曲线是重合的，而扭曲叶片则不具有这一特点。由于叶片工作面与后盖板内表面相交曲线有最大包角，在平面上，绘形叶片工作面投影实质上是绘形叶片工作面与后盖板内表面的相交曲线的平面投影。

这一平面投影曲线显然应满足如图2所示的边界条件：平面曲线应位于平面上半径分别为R2、R1B的两个同心圆之间，曲线在出口与进口处的两切线与圆周的两切线的夹角分别为β2、β1。

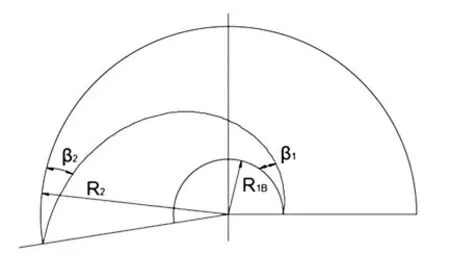
图2 叶片平面投影图Fig.2 Plane view of blade

2 单圆弧投影绘形新方法

下面给出满足上述边界条件的单圆弧曲线两种绘形新方法。

2.1 方法一概述

如图3所示，R1、R2、β1、β2已知。

图3 单圆弧曲线绘形Fig.3 Single circular arc drawing

1）绘小圆半径OK，与大圆半径OB夹角为β1+β2；

2）延长BK交小圆于另一点A；

3）过B点作BG与大圆半径OB夹角，为β2；

4）作BA中垂线，交BG于G，则有GA=GB；

5）以G为圆心，GA（GB）为半径，作弧过A和B，此弧即为所求。

下面证明这样绘形的曲线满足给定的边界条件，因而是一条可行曲线。

如图4所示，在曲线出口处，有以G为圆心、GB为半径的一圆弧，在B点作BM与这一圆弧相切，那么BM⊥GB。

图4 投影曲线的出口结构Fig.4 The exit structure of the projection curve

由于BN与大圆相切，从而BN⊥OB，那么∠NBM就是叶片出口安放角，且∠NBM=π/2－∠OBM，又因∠GBO=π/2－∠OBM，所以∠NBM=∠OBM-β2，即叶片出口角等于给定值。

如图5所示，在曲线进口处，作AM垂直于GA，AN垂直于OA，则AN是与小圆相切的圆周方向，AM是曲线进口处切线方向，∠NAM是叶片进口安放角。由于∠NAM和∠OAG都与∠GAN互余，因而∠NAM=∠OAG。

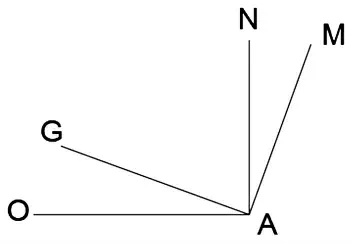
图5 投影曲线进口结构Fig.5 Inlet structure of projection curve

下面只需要证明∠OAG=β2。在图3中，由于G点是AB中垂线上的一点，由此GA=GB，进一步还有∠GAB=∠GBA，且：

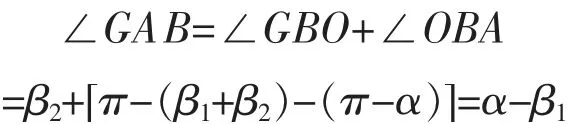
上式中，α是等腰三角形OKA的底角。则∠GAB=∠GBA=α-β1。

又∠OAG+∠GAB=∠OAK，即∠OAG+α-β1=α，故∠OAG=β1，从而∠NAM=∠OAG=β1。

由此可见，所绘圆弧两端点分别在大、小圆上，且曲线在与两圆交点处的切线方向是要求的方向，因而这是一条满足边界条件的、可行的投影曲线。

2.2 方法二概述

在图3中，R1、R2、β1、β2已知。

1）绘小圆半径OK，与大圆半径OB夹角为β1+β2；2）延长BK交小圆于另一点A；

3）过B作BG与大圆半径OB夹角为β2；4）过A作AG与小圆半径OA夹角为β1；5）设BG、AG交于G点，则有GA=GB；6）以G点为圆心，GA（GB）为半径作弧过A、B两点，这段弧就是叶片的表面投影，如图3所示。

下面只需要证明GA=GB，即可证明该曲线为可绘制曲线，且曲线为叶片表面的平面投影。

在图3中，设等腰三角形OAK底角大小为α。易得：

另一方面，∠GAB=α-∠GAO=α-β1，从而三角形GAB是等腰三角形，即GA=GB。

综上，以G为圆心、以GA（GB）为半径可以绘形一圆弧与大、小圆相交。由方法一，两交点处曲线的切线与圆周切线的夹角正是给定的叶片安放角。因此，根据本方法，不仅绘形曲线是可行的，且所绘曲线满足给定的边界条件。

3 叶片包角的计算

叶片包角是叶片的一个重要几何指标，这一角度值关系到叶片间流道的扩散度和叶片摩擦面积，因而与叶片水力效率关联密切。下面将导出以叶片进出口边界条件表示的这一角度计算式。

在图3的三角形OBK中，由余弦定理，有：

在同一三角形中，由正弦定理，有：上式即：

令等腰三角形OAK的底角∠OKA=α，由于α是三角形OBK的一个外角，因而有：

等腰三角形的顶角∠KOA显然为：

由此得到叶片包角∠BOA的最终计算式：

4 总结

单圆弧是使用最早也最普遍的圆柱形叶片型线。文中给出了这种型线两种独立的绘形新方法，并以数学分析方法证明了这样形成的平面曲线满足给定的边界条件，因而方法是可行的。同时，导出了这种曲线以其边界条件表达的包角表达式。