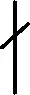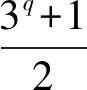具有S-拟正规子群的有限群

邓 燕, 孟 伟

(1.云南民族大学 数学与计算机科学学院,云南 昆明 650550;2.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

设G是有限群,称G的子群K和H是可置换的,如果KH=HK,即KH为G的子群.显然，对于G的正规子群N，N与G的所有子群可置换， 但反之不一定成立. Ore[1]引入了拟正规子群的概念: 称子群H为G的拟正规子群, 如果H与G的所有子群可置换. 作为拟正规子群的推广, Kegel[2]定义了S-拟正规子群.

定义1[2]设G是有限群,H为G的子群.称H是G的S-拟正规子群，如果子群H与G的所有Sylow子群可置换，即对任意的P∈Syl(G), 有HP=PH.

素数幂阶子群的S-拟正规性对有限群结构有着重要的影响(见文献[3-10]). G的素数阶子群称为G的极小子群.2009年, Asaad[4]研究了每个极小子群皆为S-拟正规子群的有限群性质.他称这类群为MS-群，证明了MS-群必可解. 进一步地，引入如下群类.

定义2[4]设G是有限群.如果G不为MS-群，但G的每个真子群皆为MS-群，那么称G为极小非MS-群.

Asaad[4]证明了极小非MS-群必可解以及群阶的素因子个数为2, 并给出了极小非MS-群的结构.

本文作为以上研究的继续, 首先借助拟单群的Schur乘子，给出了极小非MS-群可解的一个新证明; 然后, 用可解群的Sylow系证明了极小非MS-群的素因子个数为2. 证明的方法和技巧，比Assad的证明更简洁. 最后， 本文研究了二极大子群皆为MS-群的有限群.

文中所涉及到的群皆是有限群,没有特别说明的概念和符号皆是标准的.此外,用π(G)表示整除|G|的所有素因子的集合；Zn表示n阶循环群；A×B表示A与B的直积；A:B表示正规子群A被非正规子群B的扩张.

1 预备引理

引理1[2]设G是有限群，H与K是G的子群.

(1)若H≤K≤G,H在G中S-拟正规,则H在K中S-拟正规.

(2)若H在G中S-拟正规,则H◁◁G.

引理2设G是有限群,H为G的p-子群,对某个素数p.若Op(G)≤NG(H),则H在G中S-拟正规.

证明因为Op(G)≤NG(H),Q≤Op(G)≤NG(H),故当(q,p)=1时对每一个Q∈Sylq(G)都有QH=HQ.令P∈Sylp(G),H≤P,显然H◁◁P.因为G=Op(G)P,故H◁◁G,且H≤Op(G).因此,H≤S对任意的S∈Sylp(G)有HS=SH=S.证得H在G中S-拟正规.

引理3[4]若G是MS-群,则G可解.

引理4令G为2n阶二面体群，则

(1)G为MS-群当且仅当n=2f.

(2)G为极小非MS-群当且仅当n=p为奇素数.

证明(1)当n=2f时G为2-群, 此时G幂零,故G为MS-群.反之，假设G为MS-群.若n≠2f, 则存在奇素数p为n的因子.故G有一2p阶二面体子群H, 但H不是MS-群,矛盾.因此n=2f.

(2)与(1)证明类似.

引理5设G≅A4为4个文字上的交错群, 则G为极小非MS-群.

证明由于A4为极小非幂零群, 故A4为极小非MS-群.

引理6[11]设G为极小单群,(i.e.,G为非交换单群,但G的每个真子群可解).则G同构于下列单群之一:

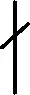
(2)PSL(2,3q),q为奇素数.

(3)PSL(2,2q),q为素数.

(4)Suzuki群Sz(2q),q为奇素数.

(5)PSL(3,3).

1.1 极小非MS-群可解性的新证明

定理1设G是一个极小非MS-群, 则G可解.

证明假设G非可解.根据定理假设知,G的每个真子群为MS-群.应用引理3，可知G的每个真子群皆为可解群.令Φ(G)为G的Frattini-子群, 即G的所有极大子群的交.那么G/Φ(G)的每个真子群皆可解.由于Φ(G)是幂零群，可得G/Φ(G)为极小单群.设C为Φ(G)的2-补, 则有C◁G且C幂零. 证明将分以下四步进行.

步骤1C≤Z(G).

对任意的p∈π(C), 设P是C的Sylowp-子群, 则P◁G.任取P的p阶子群H,由Φ(G)的幂零性, 可知H◁◁G.从而有H≤OP(G)[12,Lemma8.6(a)]. 任取q∈π(G)且q≠p, 并令Q∈Sylq(G), 则有Op(G)Q

步骤2C=1.

步骤3G/Φ(G)中的每一个2np阶子群均为2-幂零的.

假设G有一子群R满足,Φ(G)≤R且R/Φ(G)为2np阶的非2-幂零群.那么R必包含一个2mp阶的极小非2-幂零子群D.由It定理[13, IV.5.4]可知,D=T:P为内幂零群, 其中T为D的正规Sylow2-子群, |P|=p.由于G非可解, 故D为G的真子群.所以D是一个MS-群.因此P在D中S-拟正规，应用引理1(2)可知P是D的一个次正规子群.注意到P是D一个Sylow-子群, 所以P为D的一个正规子群.这导致D是一个幂零群，与D内幂零相矛盾.故G/Φ(G)中的每一个2np阶子群均为2-幂零的.

步骤4最终的矛盾.

因为G/Φ(G)为非交换单群,所以G/Φ(G)同构于引理6中的单群之一.

如果G/Φ(G)同构于PSL(3,3),PSL(2,3q)和PSL(2,p)这3类群之一, 那么G/Φ(G)将包含一个与A4同构的子群.但A4是非2-幂零的, 这与步骤3相矛盾.故G/Φ(G)不可能与这3类单群同构.

如果G/Φ(G)同构与Sz(2q)或PSL(2,2q), 那么G/Φ(G)为一奇度数的Zassenhaus群, 并且其点稳定子群是一个Frobenius核为2-群的Frobenius群. 显然这个点稳定子群不是一个2-幂零群, 亦与步骤3相矛盾. 所以G/Φ(G) 也不可能与这两类单群同构.

综上可知,G必是可解群.

定理2设G是一个极小非MS-群, 则|π(G)|=2.

证明设G是一个极小非MS-群， 根据定理1可知，G必可解.由于p-群必是MS-群, 故|π(G)|≥2.假设|π(G)|>2.令π(G)={p1,p2,…,pr},其中p1

任取G的一个极小子群H.不失一般性，可假设H≤P1.由于|π(G)|>2，所以对任意i∈{2,…,r},P1Pi是G的真子群.由定理假设知,P1Pi是MS-群.因此,H在P1Pi中S-拟正规.特别地,HPi≤P1Pi

1.2 二极大子群皆为MS-群的有限群

定理3设G是一个可解群.如果G非MS-群, 但G的每个二极大子群皆为MS-群，那么|π(G)|=2或3.

证明设G是一个非MS-群.根据定理假设知，G的每个极大子群要么为MS-群，要么为极小非MS-群.如果G所有的极大子群皆为MS-群，那么G是一个极小非MS-群.由定理2知，|π(G)|=2.

接下来假设G有一个极大子群M满足M不是MS-群.由上面讨论可知，M是一个极小非MS-群.再次应用定理2可知|π(M)|=2.由于G是可解群，则|G:M|是某个素数方幂.|π(M)|=2迫使|π(G)|=2或3.

定理4设G是一个有限非交换单群.如果G的每个二极大子群皆为MS-群, 那么G≅A5.

证明 设G为非交换单群.任取G的极大子群M，根据定理假设知,M要么为MS-群, 要么为极小非MS-群.应用引理3和定理1可知,M均可解.因此,G的所有真子群可解,从而G为极小单群.根据引理6可知,G必同构于下列5类单群之一.

(2)PSL(2,3q),q为奇素数.

(3)PSL(2,2q),q为素数.

(4)Suzuki群Sz(2q),q为奇素数.

(5)PSL(3,3).

断言1GPSL(2,3q),q为奇素数.

断言2GSz(2q),q为奇素数.

假设G≅Sz(2q).首先,G包含一阶为2·(2q-1)的二面体群子群.由引理4得(2q-1)为素数, 以及G包含一阶为22q(2q-1)的Frobenius-子群M.且M有2q-1阶循环补H,以及22q阶核K.因为K非交换,Z(K)H为M的真子群.因此由假设得Z(K)H为MS-群.H在HZ(K)中S-拟正规,由引理1(2)得H次正规于HZ(K).又因H为HZ(K)的Hall-子群,则H◁Z(K)H且Z(K)H=Z(K)×H.因此对任意的对合x∈Z(K)有H≤CM(x). 但是由[15 Theorem7.6(iv), p.38]有CM(x)≤K,矛盾.故GSz(2q).

断言3GPSL(3,3)

假设G≅PSL(3,3),则G包含一个极大子群同构于S4.显然A4为S4的极大子群.由引理5可知,A4为极小非MS-群,矛盾.故GPSL(3,3).

综上,G同构于PSL(2,p)或PSL(2,2q).

因此必有4|p-1且由引理4得p-1=2q.故

p2-1=(p-1)(p+1)=2q(2q+2)=2q+1(2q-1+1).

如果q≥3,则16|p2-1,矛盾.故q=2, 迫使p=5.所以G≅PSL(2,5)≅A5.

假设G≅PSL(2,2q), 此时G仍包含2个二面体子群D1和D2.并且|D1|=2·(2q+1)以及|D2|=2·(2q-1).由引理4得2q+1和2q-1皆为素数, 这迫使q=2.因此G≅PSL(2,22)≅A5.

反之,若G≅A5.那么G的极大子群同构于A4,S3,D10三者之一.由引理4和引理5得G的二极大子群均为MS-群.因此G满足命题假设.