巧用生活经验引导学生发现有理数的加法法则

杨辉

有理数的加法对于初学者来说比较抽象，学生比较难以掌握，尤其是学生刚刚接触负数，所以理解起来比较吃力，特别是正负号的选取，学生更是一塌糊涂。为了使学生能更好的掌握这节知识，在结合地方的实际情况，我巧用学生生活中的经历来引导学生发现有理数的加法法则，下面我将对我的教学过程进行一个分享。

首先，我将对地方民情进行分析。我所在的学校是一所农村中学，这里的学生都来自农村，他们多数人都生活在农村，自身家庭条件有限，学习条件弱，导致学生基础较弱，尤其是数学学科，底子薄，往往在有理数的运算这节掌握不好。最后到后面的相反数、合并同类项及化简求值等内容的时候，学生就会出现呢非常模糊的现象，最后学生越学越昏，最后就放弃学习数学。这里学生的生活圈子也不广，没有到过大城市，也很少与外界接触，更多的生活圈子就是跟随自己的父母或爷爷奶奶到田里地理干活，然后再将自己家种的水果和蔬菜盘到本地的街上来贩卖。在这个过程中，有的家长还会去跟小商贩批发一些商品来贩卖，久而久之，这里的学生也接触到一些商品贩卖的规则，我于是就巧用这个生活经验，巧妙解决学生学习有理数的加法的困难。

其次，很好的把握情景创设。第一、在上新课之前，先回顾上节的正负数及正负数的表示，因为本节的一个关键点就是正负数的表示。第二、复习一下分数的大小比较及分数的加减法，特别是巧用分母为“1”;分数的运算一直是中学生的一个软肋。第三就是探索新知的环节：让学生当老板来作生意，引导学生如何来记账。提醒学生我们在作生意的时候，有赚钱的时候，也有亏本的时候，我们已经学过正数和负数，赚钱就记为正（+），那亏本呢？亏本就记为负（-）。将学生分组进行抢答和讨论，使学生即可以产生竞争的意识，又可以有讨论的空间。

让学生完成下面问题：

1、昨天作生意赚了1000元记为“+1000”，那么今天亏了800元又该怎么表示？两天的利润合起来是虧本了还是赚钱了？

2、昨天亏本2000元怎么表示？今天又亏本1600元该怎么表示？两天一起是亏本还是赚钱？若赚钱则赚了多少？若亏本则又亏了多少？

在此基础上，我们一起来完成下表，看看哪个小组最先完成。提醒学生赚钱记为正（+），亏本记为负（-），算算下面的利润，看看是亏本还是赚钱？若亏本则亏了多少？若赚钱则赚了多少？

让学生完成上表，并讨论是怎么算的？

学生总结运算的方法：第一组数据学生算出为+500元，因为学生可以快速发现两天都赚钱，最后的总利润肯定是赚钱，所以结果肯定是赚钱，结果只能记为“正”。第二组数据学生算的结果为—700元，因为学生发现两天都亏本，所以结果肯定是亏本，结果只能记为“负”;昨天亏本470元，今天亏本230元，两天共亏本700元，记为“—700”元。第三组数据中昨天亏本560元，今天赚了400元，学生发现560>400也就是亏本的钱比赚的钱多，最后的利润只能是亏本，结果只能记为负“-”;亏的钱为560—400=160元;最后的利润为“—160”元。第四组数据中学生发现昨天赚钱900元而今天则是亏本720元，赚的比亏的多（900>720），最后肯定是赚钱，记过只能记为正“+”;赚的钱为900—720=180元，最后的总利润为“+180”元。最后一组数据中学生发现赚钱和亏本的都是361元，最后的利润只能为“0”。

接着，归纳提升。你是怎么样算的？第一组都是赚钱，所以最后的结果为正“+”，把连个正数相加，可书写为+（300+200）=+500。第二组都是亏本，所以最后的结果为负“—”，把两个正数相加，可书写为—（470+230）=—700。第三组数据，通过对比发现最后的总利润为亏本，所以结果记为负“—”，并用大正数减小正数，可书写为—（560—400）=—160。第四组数据，通过对比发现最后的结果是赚钱，利润记为正“+”，再用大正数减小正数，可书写为+（900—720）=+180。最后一组数据发现利润为“0”，可书写为361+（—361）=0。

跟着，提升总结。上面提到的正数其实就是对应数字的绝对值，符号相同的时候，最后的结果符号也没有改变;符号不同的时候，最后的结果取的符号都是绝对值大的，再用大绝对值减去小绝对值。帮助学生总结结论，得出有理数的加法法则。

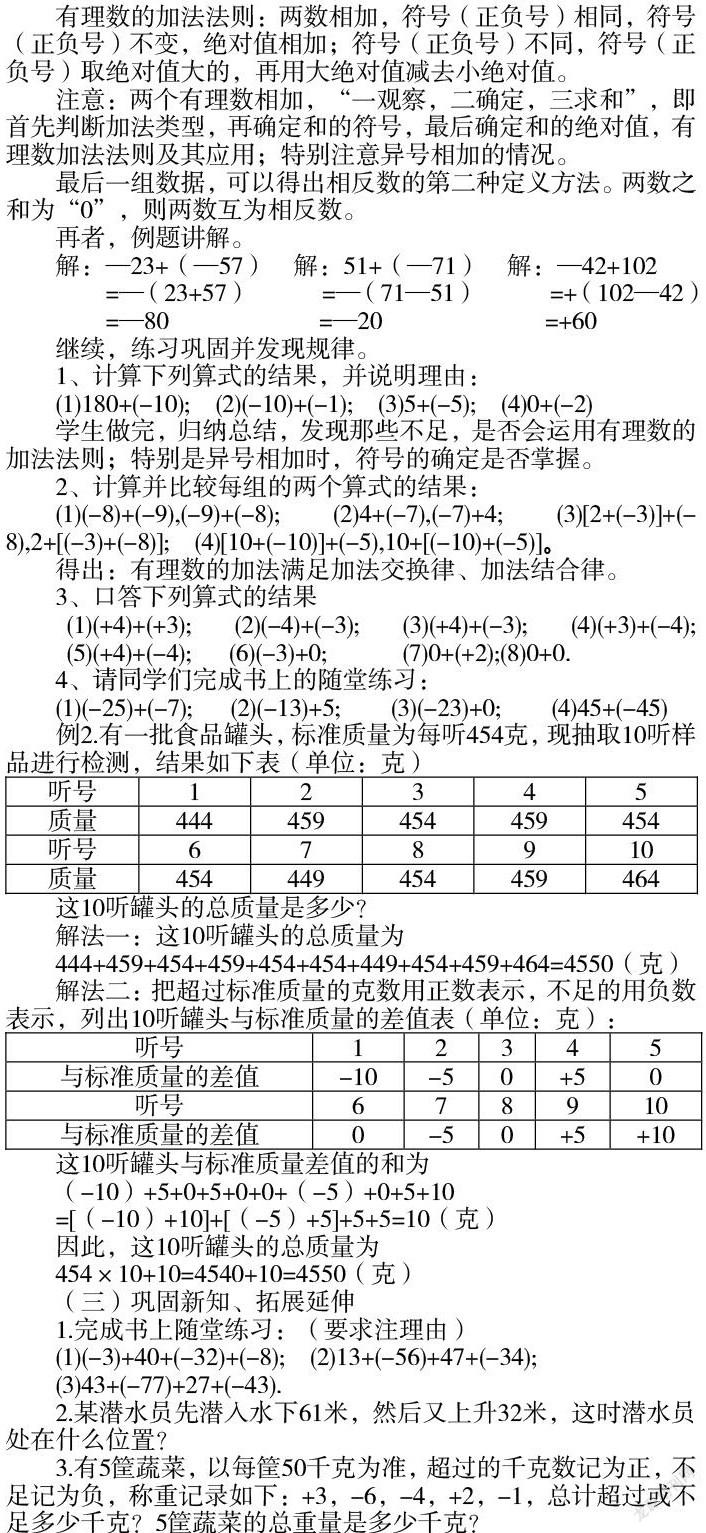
有理数的加法法则：两数相加，符号（正负号）相同，符号（正负号）不变，绝对值相加;符号（正负号）不同，符号（正负号）取绝对值大的，再用大绝对值减去小绝对值。

注意：两个有理数相加，“一观察，二确定，三求和”，即首先判断加法类型，再确定和的符号，最后确定和的绝对值，有理数加法法则及其应用;特别注意异号相加的情况。

最后一组数据，可以得出相反数的第二种定义方法。两数之和为“0”，则两数互为相反数。

2.某潜水员先潜入水下61米，然后又上升32米，这时潜水员处在什么位置？

3.有5筐蔬菜，以每筐50千克为准，超过的千克数记为正，不足记为负，称重记录如下：+3，-6，-4，+2，-1，总计超过或不足多少千克？5筐蔬菜的总重量是多少千克？

（四）课堂小结：两个有理数相加，“一观察，二确定，三求和”，即首先判断加法类型，再确定和的符号，最后确定和的绝对值，有理数加法法则及其应用。注意异号的情况。

（五）作业布置：P38习题2.5第一大题。

板书设计

有理数的加法

1、有理数的加法法则

2、相反数的第二种定义法

3、有理数的加法法则满足加法交换律、加法结合律。