不同预负荷对椭圆滑动轴承的静动特性的影响

郑帮龙 雷泽勇 朱挺 陈泳清

摘要：流体动压径向滑动轴承以润滑油为工作介质实现重载转子的润滑，在重型和大型以及超大型机械中应用广泛。建立椭圆滑动轴承的径向流体动压滑动数值模型，通过Dyrobes软件分析不同预负荷条件下椭圆滑动轴承对油膜刚度与阻尼、油膜压力、Sommerfeld数和雷诺数、摩擦功耗的影响。分析表明适当的增加预负荷能改善润滑条件，第二油楔面的形成有利于增加转子的稳定性。上述分析结果对椭圆滑动轴承的设计提供了设计参考依据。

关键词：承载能力;预负荷系数;刚度与阻尼;Dyrobes

中图分类号：O347.6                                      文献标识码：A                                  文章编号：1674-957X（2021）11-0054-03

0  引言

在转动机械的转子轴承系统中，除了转子属于转动机械的核心部件外，轴承也是重要部件，其承担着关键的支撑转子作用，性能直接影响了系统的稳定性。由于改动转子参数难度较大，设计适用于系统的轴承对提高整个系统的稳定性，有着较为重要的作用，同时滑动轴承的结构简单、承载能力大、壽命长的特点[1]，广泛的运用于中大型电机、汽轮机等旋转机械中。随着电机、燃汽轮机的装机容量不断增大，对滑动轴承的承载要求不断的提高，传统的圆形滑动轴承由于形成的楔形动压区域单一，瓦形并不能很好散失润滑油摩擦热等，限制了圆形径向滑动轴承的发展，为了更好的满足旋转机械装机容量的大型化，一种通过改变圆形瓦形状的椭圆瓦在实际中得到应用。现通过Dyrobes软件建立流体动压模型，研究不同预负荷条件下椭圆滑动轴承的静动特性。

1  数值计算模型建立

1.1 几何模型的建立

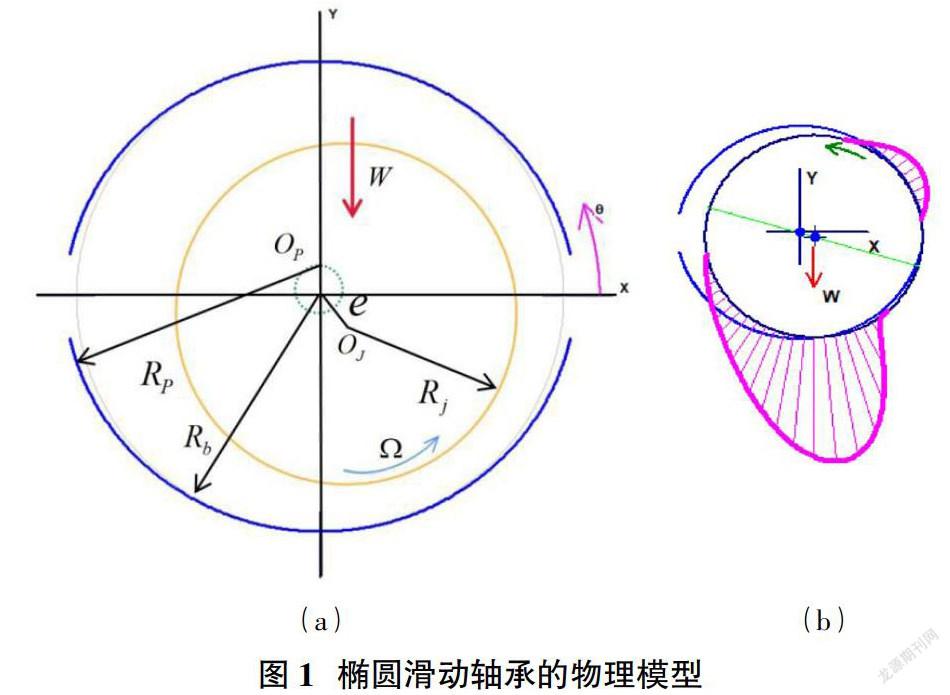
计算所用椭圆滑动轴承的几何模型如图1所示，以某38兆瓦异步电机椭圆滑动轴承为基本设计参数，轴颈转速为1496rpm，轴颈名义半径为335mm，相对间隙为0.8‰，径向载荷为123448N，供油油温为40℃。实际的轴承与轴瓦相对间隙很小，为了解释说明，滑动轴承的相对间隙进行了夸大处理。图1（a）为椭圆滑动轴承几何参数。图1（b）为椭圆瓦流体动压润滑轴承的二维油压分布示意图。

RP轴瓦的加工半径，Rb为轴瓦的装配半径，Rj为轴颈的半径，Cb为装配间隙，CP为加工间隙，预负荷系数，，。

1.2 椭圆滑动轴承的数值计算的基本原理

1.2.1 流体动压雷诺方程

流体动压油膜压力的计算主要通过一系列的合理性的假设，运用Navier-Stokes动量方程和连续性方程表示出不可压缩Reynolds方程，一些学者针对不同边界条件得出不同形式的雷诺方程[2]～[7]，本文采用修正后的Reynolds方程[2]：

Gx、Gy是修正后的的湍流系数，μ润滑油动力粘度，h是相对应压力处的油膜厚度，U为轴颈线速度。

1.2.2 椭圆滑动轴承动力学方程

滑动轴承的流体动压的油膜特性相当于一个刚度和阻尼的动力学系统，把坐标原点设在轴颈中心的静平衡位置其动力学微分方程[8]～[9]：

其中为[K]和[C]刚度系数矩阵，阻尼系数矩阵

2  不同预负荷条件下数值计算

2.1 数值计算

计算所用的椭圆滑动轴承的预负荷系数取值为m=0.3：0.1：0.8，步距为0.1从0.3开始到0.8的一组数据，将设计的参数输入Dyrobes中划分油膜网格。考虑实际情况，椭圆滑动轴承采用的是双向油槽供油，采用雷诺边界作为动压油膜的边界条件，数值算法采用有限元差分的方法对雷诺方程进行求解。

计算所得椭圆滑动轴承油膜压力分布图如图2所示，可以看出压力云图的呈现发散的流光区，此区域为动压形成区;在不同预负荷条件下上瓦和下瓦的油膜压力呈现不同的变化，可以看出随着预负荷的增大其第二油楔范围变大。说明预负荷对承载能力有影响，因预负荷变大，轴颈尺寸不发生改变时，轴承与轴颈的间隙变大油膜实际的承压面减小，在外载荷不变的条件下油膜承压区域变小油膜压力增大。

2.2 润滑条件和流体状态分析

由图3可知不同预负荷与Sommerfeld系数存在关系，Sommerfeld数反应轴瓦与轴颈间的润滑状态[10]，表明随着预负荷的增大润滑条件得到改善。由图4知随着预负荷的增大Reynolds数下降，Reynolds数较小时粘滞力对流场的影响大于惯性力，流场的扰动会因粘滞力而衰减，流体流动较稳定[11]。

2.3 几何参数分析

图4和图5显示了不同预负荷对偏心率和偏位角的影响，可以看出随着预负荷系数的增加油膜受到的挤压更加显著，最小油膜厚度变小，楔形效应更加明显[12]。结合图1的压力云图可以看出偏心率增大，第二油楔效应更明显，图6曲线知预负荷0.3-0.7时，偏位角随着预负荷系数增大而减小，分析原因由于第二油楔作用增加了水平方向的稳定性。

2.4 功耗损失

图7 随着预负荷增大摩擦功耗先减小后增大，表明当预负荷较小时楔形进油区域较小，供油量较少随着预负荷的变大楔形区变大，但与此同时第二油楔区也在扩大这部分增加的功耗，由曲线知其影响大于楔形区进油量的影响。

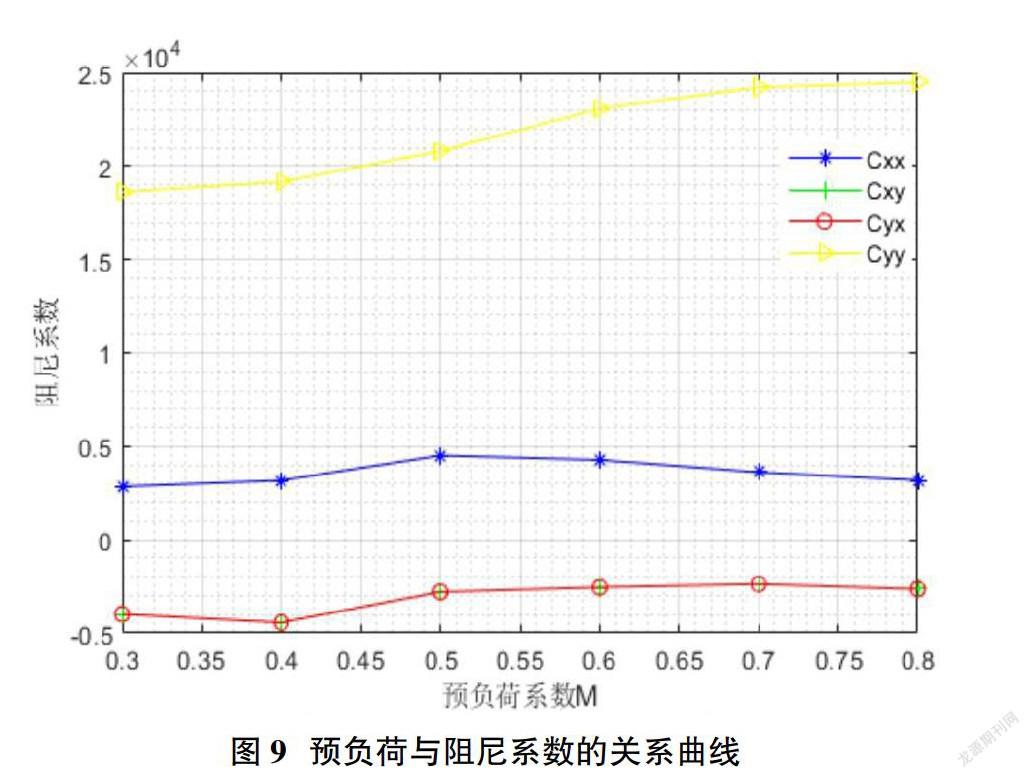
2.5 椭圆滑动轴承的动特性分析