浅谈借助分支图解决数学问题

鲍妙森

摘要：在小学数学中，解决问题的重要性不言而喻，本文结合具体问题，借助分支图对问题进行清晰合理的分析，阐述解决问题中通过审题并列出式子的过程，归纳出基于核心素养的审题列式策略，以提高学生的解题能力，培养应用意识和创新意识。

关键词：小学数学;解决问题;列式

“解决问题”考察了学生的各项综合能力，是小学数学非常关键的内容，呈现形式往往是情境丰富，背景鲜活，文字冗长，类型多变，对于正处于由形象思维向抽象思维过渡的小学生来说，理解起来困难较大。如果不掌握一种直观而又科学的分析方法，不断开拓解题思路，提高解题能力，长此以往将极大地挫伤学生学习的积极性。

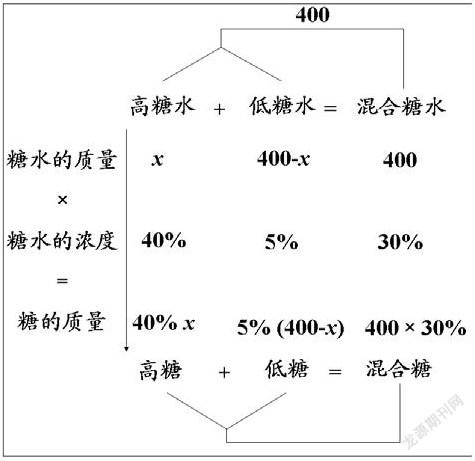
问题 ：用浓度45%和5%的糖水配制成浓度为30%的糖水400克，则需要这两种糖水各多少克？

这个问题有一定的难度，其中的内涵需要借助分支图加以深刻的理解，从而归纳出解决问题中审题并列出式子的通用方法，摆脱“教师难教，学生难学”的现象。

一、明确各个量，构建数量关系

解决问题所需要的信息要从问题入手寻找，在明确问题的基础上收集信息，引导学生整理问题中的各个量，立足于解决问题的本质。仔细审题是正确解题的前提，需要对问题进行审读，分析题目中的相关对象，把题目中的各个量提取出来，分析量与量之间的关系，即构建数量关系。

1.明确对象，梳理数量

学生在解决问题时，必须先要把题中的数量关系理清楚。数量关系是解决问题的灵魂，任何问题都是通过数量关系来体现的。在解决问题时只要理清数量关系，问题也就迎刃而解了。

这是糖水配比问题，题目中的对象：

（1）浓度45%的糖水;

（2）浓度为5%的糖水;

（3）“混合”之后30%的糖水，

为了方便起见，我们记作高糖水，低糖水，混合糖水，类似的，如其中的含糖量分别记为高糖，低糖，混合糖。

题目中的量相对清晰，就是糖的质量，水的质量，糖水的质量，糖水的溶度。

2.合理分类，搭建关系

一般解决问题题型都是由已知条件和问题两部分组成，对已知信息进行合理分类，分析数量之间的关系是审题的核心环节。由于小学生阅读理解的能力有限，错误判断题意，因此要引导学生关注关键词，以及重要句中所涉及的数量关系。

3.正确选择，建立联系

引导学生从题目中提炼出有用的数学信息，根据题意进行合适的选择，忽略与本题无关的数量关系，推敲题目中的字词，发掘出隐含条件，排除一些冗余条件。较为复杂的问题还需要构建不同数量关系之间的内在联系，从而为后续解题奠定必要的基础。

梳理出解决问题相关的数量关系，这个问题有关的数量关系是：

② 糖水的质量×糖水的浓度=糖的质量;

③ 高糖+低糖=混合糖;

⑤ 高糖水+低糖水=混合糖水，

這个时候我们需要思考这三个数量关系之间存在着必然的联系，并搭建它们之间的联系，依托“②糖水的质量×糖水的浓度=糖的质量”，可以把“③高糖+低糖=混合糖”和“⑤高糖水+低糖水=混合糖水”这两个貌似相差甚远的两个数量关系有效的连接起来。

学生思得如何，需要教师引导学生有条理、有逻辑地思考问题，使学生能够全面分析解题的思路，促进学生逻辑思维能力的发展，提高学生运用数学知识、解决实际问题的能力教师不但要留给学生充分思考的余地，使学生主动而积极地产生遐想，引发思维的火花，刚要关注每一个学生的思维活动，为学生提供独立思考的机会，力求“实现不同的人在数学上都得到不同的发展”。

二、表示各个量，形成分析策略

1.搭建主框架

主框架的搭建其实是建立在数量关系以及彼此关系的基础上，用分支图可以更加清晰展现各种量之间的联系。

2.表示各个量

任何问题在题目中都存在已知量和未知量，有些量是比较明显的，可以直接列举出来;但是有些量不太明显，则可以借助完整数量关系逆向导出缺失量。利用分支图分析问题时，学生可以通过读题来明确问题，寻求条件，从而将已知量和未知量表示在分支图中，有助于实现学生的思维由外化至内化的转化过程。例如本题有关的关系：② 糖水的质量×糖水的浓度=糖的质量;

③ 高糖+低糖=混合糖;

⑤ 高糖水+低糖水=混合糖水，

根据缺失量可以有计划的设未知数，利用数量关系表示各个量，有的时候需要把数量关系进行变形来表示不同的量，这个要根据设立的未知数，结合题意进行合理分析。本题我们可以设高糖水为x克，因为混合糖水为400克，所以低糖水可以表示为（400-x）克，糖水的浓度都是知道的，可以顺次填入，通过糖水的质量×糖水的浓度=糖的质量，表示出糖的质量，由此分支图中的所有空缺处都填入了表示各个量有关的数或含字母的式子。

3.列出关系式

有些问题往往并不是直接地出现解答的思路，而是需要学生对问题的数量关系等进行分析才能正确地解答。分析和抽象对于正确地列出式子，解决实际问题是至关重要的。

根据高糖+低糖=混合糖，从分支图中，可以很容易的列出式子。解决问题需要相应的策略来支撑对问题的分析、思考，让学生了解和形成解决问题的一些基本策略。建构主义认为，学生的建构不是教师传授的结果，而是通过亲历、通过与学习环境的交互作用来实现的。从学习角度看，学习既是一个内化的过程，同时也是一个外化的过程。

借助分支图法解决问题，可以把思维过程具体清晰地呈现出来，让蕴含在题目背后各个量之间的关系跃然纸上。学生可以透过丰富的背景提炼出解决问题的脉络，通过形象直观的学习来积累活动经验，感受分析问题的殊途同归，这样即能培养学生问题解决的能力，还能提高他们的数学素养。

参考文献：

[1] 周彬.《课堂密码》[M].上海：华东师范大学出版社，2009.

[2] 中华人民共和国教育部.《义务教育数学课程标准（2011年版）》[M].北京，北京师范大学出版社，2012.

浙江省永嘉县沙头镇花坦小学 浙江 永嘉 325109