为数学教学插上翅膀

蒋素芳

在多年的初中数学教学中，笔者总觉得学生在上七年级（上）4.1《用字母表示数》的时候，学生特别感兴趣，那是由于数学课堂上教师常用多媒体播放一些数学动画及儿歌，这些都能将学生带入神奇有趣的数学世界。

一、新课课堂学习中多媒体之“有趣”

数学课中出现大量的“讨论”，如：《勾股定理》这一课中有这样一个习题：长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？将学生分组后将问题带回家思考。

讨论：1.求两点间的最短距离你想到什么？

学习经过讨论后得出：两点间的最短距离是连接这两点的线段的长度。

2.題中蚂蚁是沿长方体表面爬行，能否直接连接这两点？

经过学生讨论后在课堂上，教师可利用多媒体演示，将长方体表面展开。

3.除了这种展开方式，还有其他的展开图吗？

因为学生回家已经进行了思考，有些组的代表利用多媒体将自己的的成果进行展示，显得非常清晰明了，共得到三种类型的展开图。

4.你能利用这些展开图计算最短距离吗？

5.哪个距离才是我们这道习题的最短距离？

二、实验课堂学习中凸显多媒体之“有利”

如：在讲授《直线和圆的位置关系》这一课时的时候，利用多媒体技术可以使直线转动，产生与已知圆的相离、相切、相交的各种动态的位置关系，并在旁边显示圆的半径（R），并动态的显示圆心到直线的距离（d），学生们可以一目了然的动态的了解到直线与圆的位置关系，与圆的半径（R）、圆心到直线的距离的数量关系，使学生在观察实验的同时，推出直线和圆的位置关系与圆的半径、圆心到直线的距离之间的关系。

如：在讲授等腰三角形“三线合一”时，因传统教学较难展现其发现过程，给学生的理解造成一定的难度。利用《几何画板》软件，则可以在屏幕上作出等腰ΔABC及其顶角∠A的平分线、BC边上的高和BC边上的中线，用鼠标在屏幕上拖动ΔABC的顶点A，改变ΔABC的大小和形状（但始终保持其为等腰三角形）。此时，等腰ΔABC和"三线"在保持依存关系的前提下随之变化而变化，但在移动的过程中，学生会直观地发现存在这样的点A，使得等腰三角形顶角的平分线、底边上的高和底边上的中线三线重合。

三、复习课堂学习中展示多媒体之“有效”

传统的复习课教学中，教师把大量时间花在语言描述和板书等方面。语言陈述过多，学生抓不住重点，前后内容联系困难。而应用多媒体教学，可以将本章的知识点逐个呈现出来，构建出“知识树”。

“代数式”这部分教学内容特点：基本概念多，必须记忆的多，实际运用的多，题型变化多。通过多媒体课件呈现上面的“知识树”，学生能将本章的知识要点清晰地记住。

纵观近几年的中考试题，有关动点问题的综合试题，学生比较薄弱。若采用传统的教学，老师板书、画图、抄例题耗费大量宝贵的学习时间，而且可视性差，在一节课内容量较小的情况下，教学效果也会受到影响。

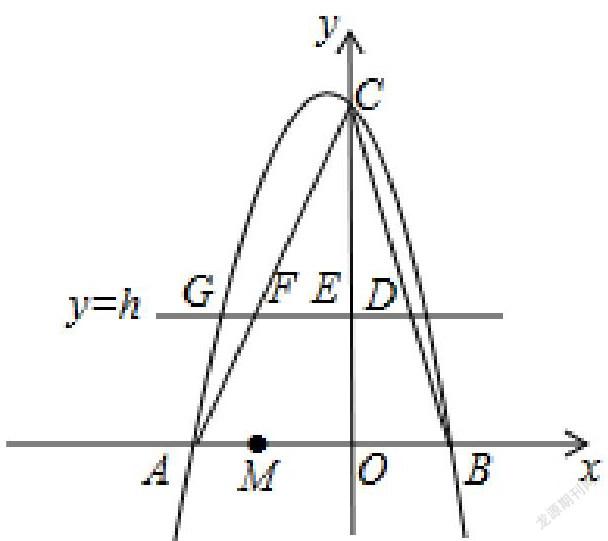
如：“二次函数”综合题

例1：如图，在平面直角坐标系中，抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0）.直线y=h（h为常数，且0

（1）求抛物线的解析式;

（2）连接BE，求h为何值时，△BDE的面积最大;

（3）已知一定点M（-2，0）.问：是否存在这样的直线y=h，使△OMF是等腰三角形？若存在，请求出h的值和点G的坐标;若不存在，请说明理由。

总之，在现代教学中利用多媒体技术是提高课堂效率的一种有效手段。但在教学中一定要突出学生的主体地位，“教师的用”与“学生的用”要有机的结合，这样才能真正促进学生自主地参与到课堂教学活动中。

参考文献：

[1]初中《数学》（7-9年级）教科书、教师教学参考用书、新课程标准

[2]王道俊.教育学[M]北京：人民教育出版社