文学作品中的逻辑推理在三视图问题中的应用

徐欢眉

1引言

2004年开始实施的《普通高中数学课程标准（实验）》将“注重提高学生的数学思维能力”列为高中数学课程十大基本理念之一，《普通高中数学课程标准（2017年版）》则将“直观想象”和“逻辑推理”列入六大数学学科核心素养之中[1].直观想象和逻辑推理（理论证明）贯穿数学学习的全过程，也是高考的重点考查方向.正如理性分析与感性认知永远不是相互割裂的两种能力，逻辑推理和直观想象也能有机结合，小则提高数学思维与探究能力，大则更好地感知世界并与世界建立联系.

如何将逻辑推理与直观想象有机结合，本文将以《空间几何体》中的三视图问题为例，利用著名文学作品《福尔摩斯探案集》中使用的逻辑，对三视图问题提出新的理解，实现逻辑推理与直观想象的辩证统一.同时，在数学课堂中引入文學内容，也是将文科和理科的有机结合，让课堂更有活力，让学生更有兴趣.

2三视图与文学作品中的逻辑推理

2.1空间几何体的三视图

在《2020年普通高等学校招生全国统一考试大纲》中对《空间几何体》的要求是“认识柱、锥、台、球及其简单组合体的结构特征，能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，了解球、棱柱、棱锥、台的表面积和体积的计算公式”.在高考中，三视图问题的常见类型大致有以下两种：

1.根据三视图还原几何体的形状，并求解几何体的表面积和体积;

2.根据几何体的部分视图求剩余部分视图.[2]

空间几何体是学生第一次系统地接触三维空间.在此之前，他们在初中阶段获得了二维空间的知识，对三维空间无限性和复杂性的认知十分有限，从平面图形到空间几何体的迁移对部分空间想象力薄弱的学生而言并非易事.

空间想象力是对客观事物空间形式的抽象思维能力[3]，对应数学学科核心素养中的直观想象.空间中图形的位置关系，立体图形的叠加与切割，都需要学生在大脑中建立起三维模型，而三视图问题则是对这种能力的综合考查，学生需要掌握平行投影和中心投影，学会在平面中表示空间图形的技能[4].

2.2文学作品中的逻辑推理

“当你排除所有不可能的部分，剩下的无论多么不可能，也一定是真相.”[5]这句名言出自柯南·道尔著名中篇小说《四签名》，其笔下的名侦探夏洛克·福尔摩斯常用此逻辑将案件解决.推理小说中就运用了大量的感性认知与理性分析，分别对应看得见的线索和看不见的推理.构成福尔摩斯演绎法的两大核心要素——观察与推理.观察是对线索的捕获、对有效信息的发现，放在数学问题中即对题目信息的获取与翻译;推理包括两大基本过程——归纳推理和演绎推理.

记结论的全集为，满足条件的结论用集合表示，不满足条件的结论用集合表示，显然， .上述引文背后的数学知识，即排除全集U中不满足条件的结论，剩下的就是集合B的补集，即集合A，也就是满足条件的结论.关键词为“所有”，只有所有不满足条件的结论构成的集合才能与满足条件的结论构成的集合互为补集.通过排除所有不满足条件的结论，我们就能得到满足条件的结论.

这种方式主要针对根据已知条件很难直接得出结论的一类问题——没有很好的空间想象力，很难通过三视图直接作出几何体的直观图;而根据已知条件，排除掉一些结论会比较容易——以某个基本几何体作为参照，根据三视图排除该参照物中肯定不存在于所求几何体上的顶点或棱，“排除所有不可能的”，关注“剩下的”，最终就能得到“真相”.这种方式结合了从三视图中获得的感性认知与推理过程中的理性分析，是直观想象与逻辑推理的有机结合.

3例题分析

3.1根据三视图还原简单几何体

3.1.1三视图中无虚线

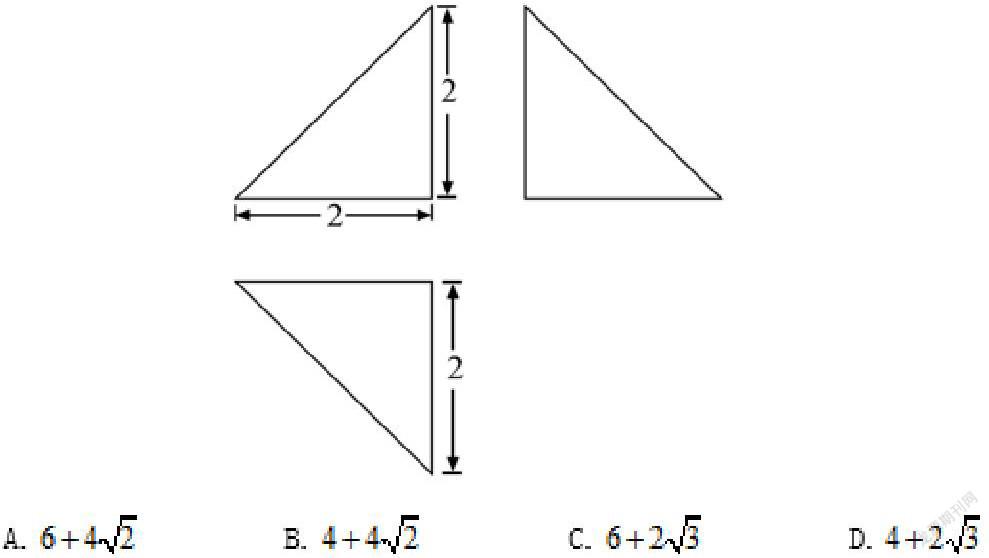
例1（2020年高考全国卷理科III卷第8题）下图为某几何体的三视图，则该几何体的表面积是（）

在该题中，由于三个视图均为三角形，结合空间几何体的结构特征的相关知识，空间想象力好的学生可以直接判断出该几何体为三棱锥并画出其直观图，进而求得该三棱锥的各条棱长及其表面积.倘若学生无法在大脑中建立起该几何体的三维模型，我们能否利用本文2.2中讲述的逻辑点，推理出该几何体原本的形状呢？

结合三视图“长对正，高平齐，宽相等”的原则，我们必能得到该几何体恰好能被放置在棱长为2的立方体中（图3-1），且该几何体的顶点均为此立方体的顶点，至于是哪些顶点构成了该几何体，我们“排除一切不可能的”，关注“剩下的”，看看是否与“真相”接近.

若规定垂直于平面为主视方向，首先，根据主视图可以判断，立方体中的顶点和不存在于该几何体中;同理，根据侧视图可以判断，顶点也不是该几何体的顶点;最后，由俯视图可知，顶点A也不存在于该几何体中，将“不可能的”点去掉，将“剩下的”点连接起来（图3-2），得到三棱锥，经检验发现，符合题干中的三视图.

除此之外，还可通过另一种方式判断剩余四个顶点确实是该几何体的顶点.由主视图和侧视图可知，棱和（不含端点）均不在该几何体中，为了满足主视图中位于上方的三角形顶点存在，则立方体中的顶点必然存在，同理可推理出其余三个顶点也必然存在.

3.1.2三视图中有虚线

根据有虚线的三视图还原几何体一直是学生不知从何入手的一类问题，对空间想象力的要求更高，往往信息量越大，题目越复杂.原则是看得见的线用实线，看不见的线用虚线.但即便知道这一原则，多数学生也不知该如何利用.如果无法想象出几何体的形状，我们依然可以试试逻辑推理的方法.

例2下图为某多面体的三视图，则该多面体的体积为________.

易知该几何体必能被放置在棱长为4的立方体中（图3-1），如上一个例子，我们首先排除不可能的点.根据主视图和俯视图可以排除顶点.同时可排除棱（不含端点）（图3-3）.在剩下的顶点中，我们可以通过同例1相似的推理，得到必然是该几何体的顶点，否则无法满足三视图.剩下暂时无法判断的顶点D，再看信息量最大的侧视图.根据“看得见的用实线”这一原则，若顶点D是该几何体的顶点，那么四边形是侧视图中能被看到的图形，也就意味着题干中侧视图的实对角线将无法体现，因此顶点D不是该几何体的顶点.至此，我们已排除了所有不可能的顶点，仅剩，这四点构成的三棱柱经检验满足题目条件（图3-4）.我们发现，利用逻辑推理得到几何体的过程中，侧视图中虚线的信息仅在检验时用到，大大降低了难度.

3.2根据三视图还原组合体

空间中的组合体有叠加式、切割式和综合式三种基本形式.叠加式组合体由多个基本几何体叠加而成，按照几何体之间接触方式的不同，可细分为相接、相切、相贯三种类型.切割式组合体可视为在基本几何体上进行切割、钻孔、挖槽后剩余部分所形成的几何体.综合式组合体为多个基本几何体的叠加及切割，是组合体中最为常见的形式.

叠加式和切割式在高考中考查得比较多，其中叠加式组合体为中低难度，考生能够根据三视图较为容易地判断出构成组合体的基本几何体的类型，进而还原出组合体的形状，判断几何特征，求解表面积与体积.切割式组合体对考生的空间想象能力要求更高，需要利用三视图中虚线实线的特征，判断出该几何体是对何种基本几何体做了怎样的切割，进而还原出组合体的形状.它与叠加式组合体不同的是，我们能从叠加式组合体的三视图中迅速辨认出常见的基本几何体，而切割式组合体的三视图无法给我们直观的信息，在运用空间想象力的同时还需要一定的逻辑推理.

3.2.1叠加式组合体

例3（2020年高考全国卷理科II卷第7题）如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M，在俯視图中对应的点为，则该端点在侧视图中对应的点为（ ）

不难发现，在该题中，组成三视图的基本几何图形为矩形，由此可辨别出该几何体由两个四棱柱相接而成，此几何体为叠加式组合体.需要注意的是，在叠加式组合体中，若分处两个几何体的两个平面共面，则相接部分的棱在三视图中无法体现（对应主视图内部并无实线）.而侧视图中的实线与虚线则告诉我们两个四棱柱的相对位置，进而得到还原后的几何体（图3-5）.因此答案为A.

3.2.2切割式组合体

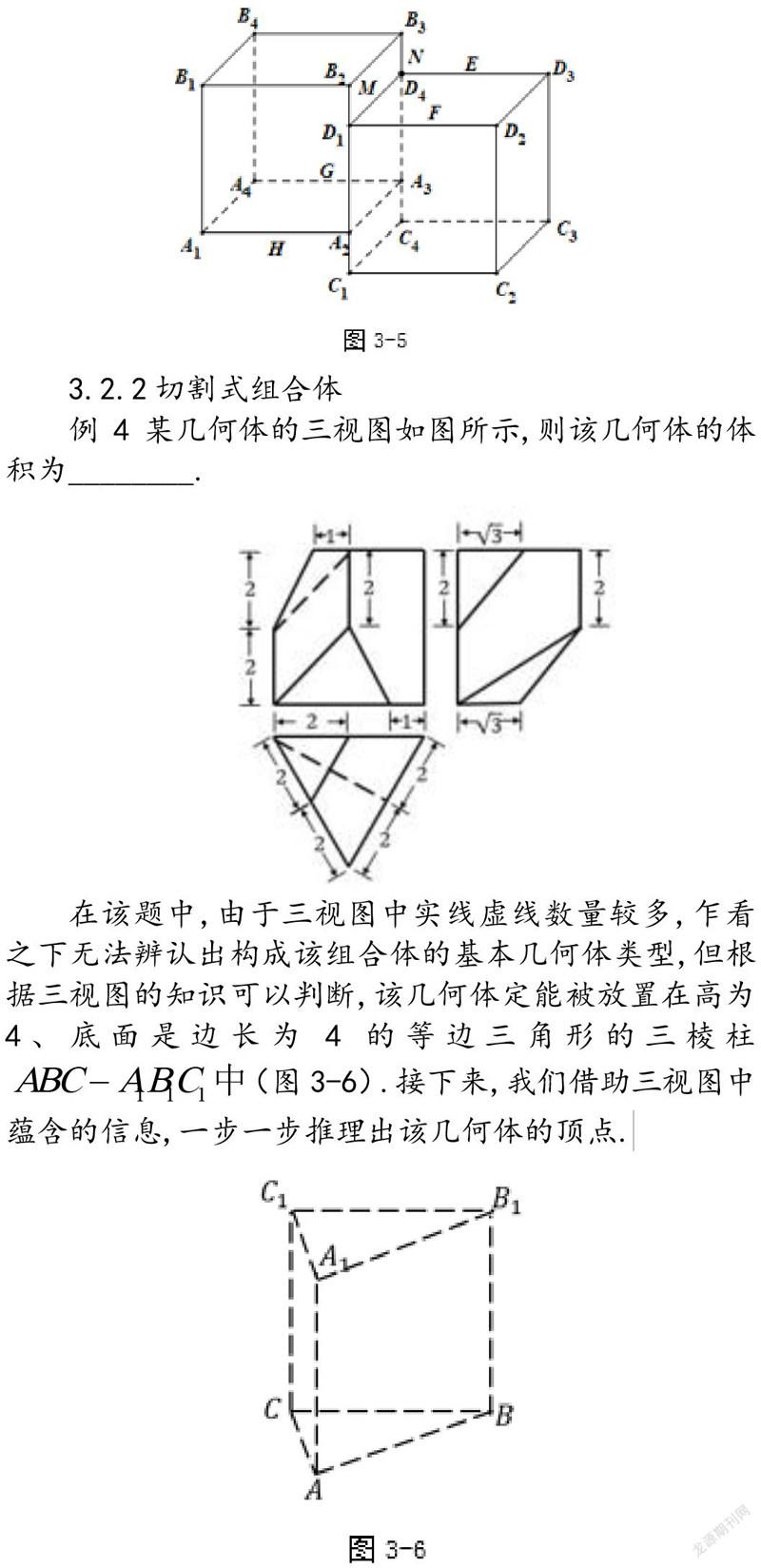
例4某几何体的三视图如图所示，则该几何体的体积为________.

在该题中，由于三视图中实线虚线数量较多，乍看之下无法辨认出构成该组合体的基本几何体类型，但根据三视图的知识可以判断，该几何体定能被放置在高为4、底面是边长为4的等边三角形的三棱柱中（图3-6）.接下来，我们借助三视图中蕴含的信息，一步一步推理出该几何体的顶点.

首先，根据主视图外部图形可视为矩形切去左上角以及俯视图内部实线可知，三棱柱中的顶点不存在于该几何体中;其次，根据侧视图外部图形可视为矩形切去右下角以及俯视图内部虚线可知，三棱柱中的顶点A不存在与该几何体中.而其余四个顶点均可推理得出存在于该几何体中.

“排除一切不可能的，关注剩下的部分”.从整体上看，所求的几何体应为三棱柱切去分别以A和为顶点的两个三棱锥.至于两个三棱锥中其余三个顶点位于三棱柱的什么位置，我们再通过三视图中的实线和虚线加以判断.

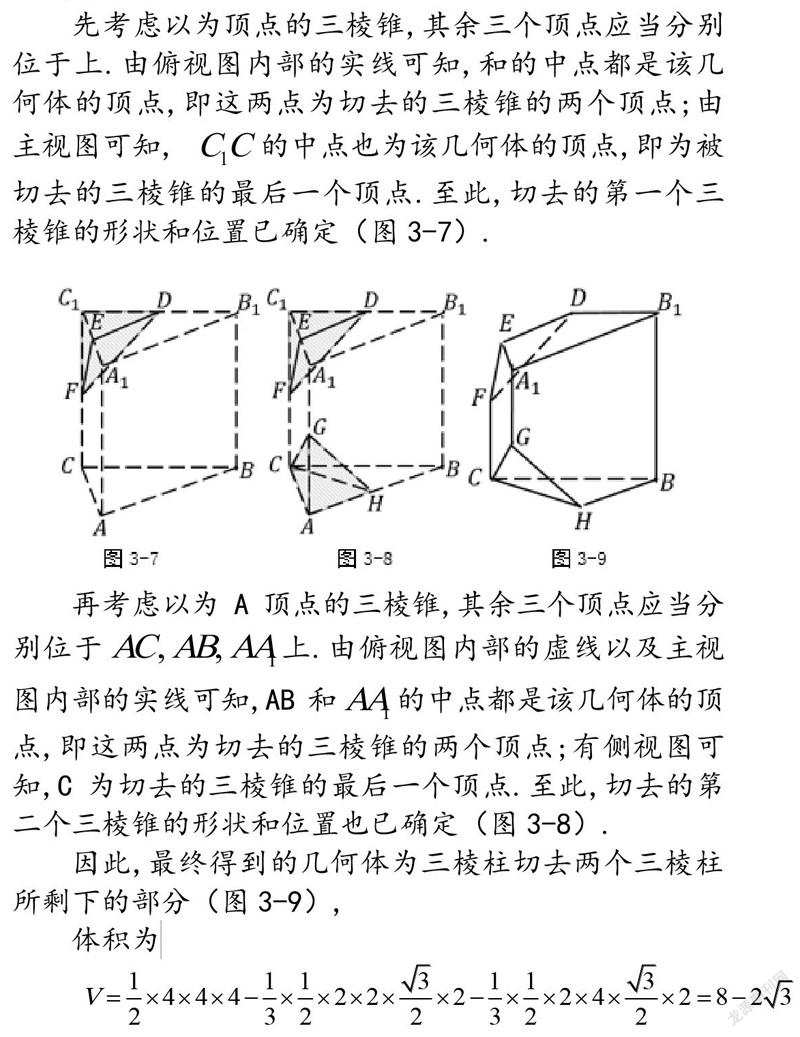
先考虑以为顶点的三棱锥，其余三个顶点应当分别位于上.由俯视图内部的实线可知，和的中点都是该几何体的顶点，即这两点为切去的三棱锥的两个顶点;由主视图可知， 的中点也为该几何体的顶点，即为被切去的三棱锥的最后一个顶点.至此，切去的第一个三棱锥的形状和位置已确定（图3-7）.

再考虑以为A顶点的三棱锥，其余三个顶点应当分别位于上.由俯视图内部的虚线以及主视图内部的实线可知，AB和的中点都是该几何体的顶点，即这两点为切去的三棱锥的两个顶点;有侧视图可知，C为切去的三棱锥的最后一个顶点.至此，切去的第二个三棱锥的形状和位置也已确定（图3-8）.

因此，最终得到的几何体为三棱柱切去两个三棱柱所剩下的部分（图3-9），体积为

4结语

世间万物紧密联系，我们想知道某件事物的本质，未必只能通过研究该事物，还可通过了解与其相关联的一切事物来探寻它的本质.知识结构是网状的，知识正迁移是快速掌握新知识的有效途径.而在知识迁移的过程中，也要充分利用核心素养之间的联系.

我们身处的世界充满了可探寻的事物，需要我们去观察，去推理.要善于发现并利用事物之间的联系，建立起感性认知与理性分析之间的桥梁.

正如柯南·道尔在小说《五个橘核》中所说，“因世间的一切就像根链条，我们只需瞧见其中一环，就可知全体的性质”

（作者单位：杭州市余杭区杭州英特外国语学校）