圆的一类中考试题解析

何婷

【摘要】本例运用执果索因、由因导果分析方法，结合思维导图教学模式，抓住常见数学模型，让学生经历条件和结论之间的双向转化思维训练，领悟解决这类问题的一般思想方法.

【关键词】试题解析;分析方法;数学模型

【题目原型】

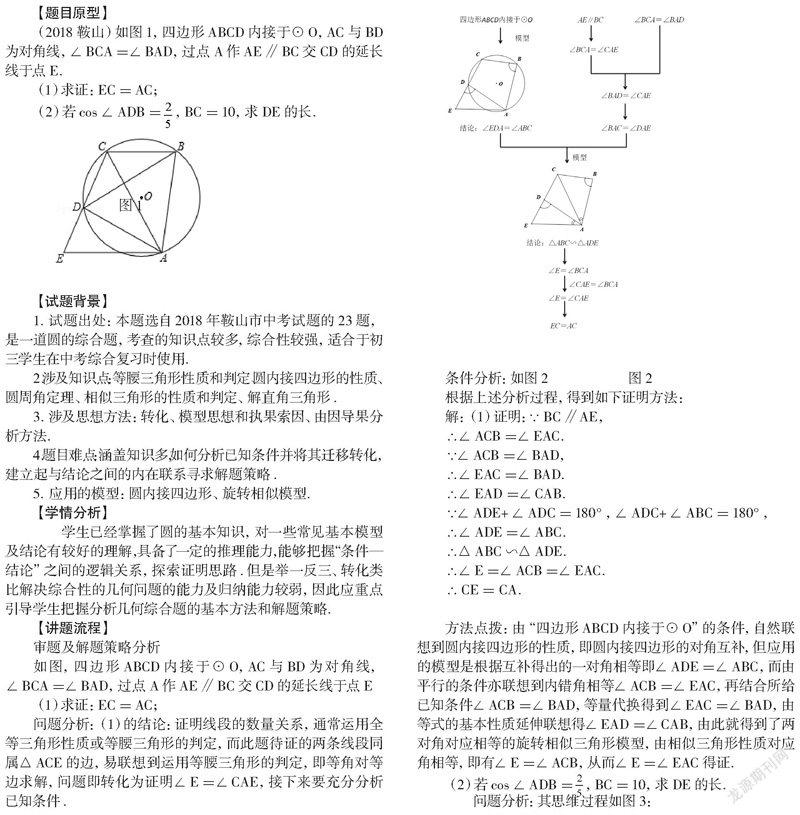
（2018鞍山）如图1，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA=∠BAD，过点A作AE∥BC交CD的延长线于点E.

（1）求证：EC=AC;

（2）若cos∠ADB=，BC=10，求DE的长.

【试题背景】

1.试题出处：本题选自2018年鞍山市中考试题的23题，是一道圆的综合题，考查的知识点较多，综合性较强，适合于初三学生在中考综合复习时使用.

2.涉及知识点：等腰三角形性质和判定、圆内接四边形的性质、圆周角定理、相似三角形的性质和判定、解直角三角形.

3.涉及思想方法：转化、模型思想和执果索因、由因导果分析方法.

4.题目难点：涵盖知识多，如何分析已知条件并将其迁移转化，建立起与结论之间的内在联系寻求解题策略.

5.应用的模型：圆内接四边形、旋转相似模型.

【学情分析】

学生已经掌握了圆的基本知识，对一些常见基本模型及结论有较好的理解，具备了一定的推理能力，能够把握“条件—结论”之间的逻辑关系，探索证明思路.但是举一反三、转化类比解决综合性的几何问题的能力及归纳能力较弱，因此应重点引导学生把握分析几何综合题的基本方法和解题策略.

【讲题流程】

审题及解题策略分析

如图，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA=∠BAD，过点A作AE∥BC交CD的延长线于点E

（1）求证：EC=AC;

问题分析：（1）的结论：证明线段的数量关系，通常运用全等三角形性质或等腰三角形的判定，而此题待证的两条线段同属△ACE的边，易联想到运用等腰三角形的判定，即等角对等边求解，问题即转化为证明∠E=∠CAE，接下来要充分分析已知条件.

条件分析：如图2

根据上述分析过程，得到如下证明方法：

解：（1）证明：∵BC∥AE，

∴∠ACB=∠EAC.

∵∠ACB=∠BAD，

∴∠EAC=∠BAD.

∴∠EAD=∠CAB.

∵∠ADE+∠ADC=180°，∠ADC+∠ABC=180°，

∴∠ADE=∠ABC.

∴△ABC∽△ADE.

∴∠E=∠ACB=∠EAC.

∴CE=CA.

方法点拨：由“四边形ABCD内接于⊙O”的条件，自然联想到圆内接四边形的性质，即圆内接四边形的对角互补，但应用的模型是根据互补得出的一对角相等即∠ADE=∠ABC，而由平行的条件亦联想到内错角相等∠ACB=∠EAC，再结合所给已知条件∠ACB=∠BAD，等量代换得到∠EAC=∠BAD，由等式的基本性质延伸联想得∠EAD=∠CAB，由此就得到了两对角对应相等的旋转相似三角形模型，由相似三角形性质对应角相等，即有∠E=∠ACB，从而∠E=∠EAC得证.

（2）若cos∠ADB=，BC=10，求DE的长.

问题分析：其思维过程如图3：

根据上述分析过程，得到如下证明方法：

解：如图4作CM⊥AE于M.

方法点拨：由条件cos∠ADB=，联想到以下思路：①可找与之相等的角转化，等角的同名三角函数值相等.②能确定直角三角形中兩边之比.③可求其他三角函数值（正弦，正切）.由圆周角定理有∠ACB=∠ADB，而由（1）知∠E=∠ACB，因此应用①方法转化角，即∠ADB=∠E，cos∠E=，可解直角三角形求线段长或得线段的比，具体如何应用要分析结论确定，但无论怎样用都要有直角三角形，因此需要引辅助线构造直角三角形，而△ACE为等腰三角形，三线合一引垂线，辅助线即为作CM⊥AE于M.结论为求DE的长，求线段长的方法有勾股定理、三角形相似、三角函数，而由第一问已经得到△ABC∽△ADE，对应边成比例发现只要确定的值，即可求

得DE长，因此由前面cos∠E=，可得，易得，进而求解.

题后反思

1.解题思路与方法解读

第二问虽然是圆的常规计算，但是综合性较强，解决问题的关键在于将求线段长度的几种常用方法，即勾股定理、三角形相似、三角函数与圆的相关知识结合起来综合应用，还要有抓住前后问联系的意识，往往第（1）问的结论要为第（2）问所用，

2.条件和模型的应用

此问运用执果索因、由因导果分析方法，由每一个条件联想出第一级结论，不能得到一级结论的条件这里称为绝对条件，如∠BCA=∠BAD，然后分析各一级结论之间、一级结论和绝对条件之间的联系，得到二级结论，再分析二级结论之间、二级结论和绝对条件之间的联系得到三级结论，依次类推找到“条件—结论”之间的逻辑关系.也可从结论入手执果索因，方法同上，但在更多的综合题中是两种分析方法结合使用.

变式训练

1.（2018锦州）如图5，在△ABC中，∠C=90°，AE平分∠BAC交BC于点E，O是AB上一点，经过A，E两点的⊙O交AB于点D，连接DE，作∠DEA的平分线EF交⊙O于点F，连接AF.

（1）求证：BC是⊙O的切线.

（2）若sin∠EFA=，AF=5，求线段AC的长.

思路点拨：（1）连接OE，根据同圆的半径相等和角平分线可得：OE∥AC，则∠BEO=∠C=90°解决问题;（2）过A作AH⊥EF于H，根据三角函数先计算AH=4，证明△AEH是等腰直角三角形，则AE=AH=8，证明△AED∽△ACE，可解决问题.此题属于圆的综合题，涉及的知识有：切线的判定与性质，相似三角形的判定与性质，锐角三角函数定义，勾股定理，以及平行线的判定与性质，综合应用以上知识运用执果索因、由因导果分析方法是解本题的关键.

2. （2018锦州二模）如图6，在△ABC中，以AC边为直径作⊙O交BC边于点D，交AB于点G，且D是BC中点，DE⊥AB，交AB于点E，交AC的延长线交于点F.

（1）求证：直线EF是⊙O的切线.

（2）若CF=3，cos∠CAB=，求⊙O的半径和线段BD的长.

思路点拨：（1）根据三角形的中位线定理证明OD∥AB，可得OD⊥EF，所以直线EF是⊙O的切线;（2）设⊙O的半径为r，根据平行线分线段成比例定理得：，可得AE的长，

并计算BE的长，证明△BDE∽△BAD，则，代入可得BD的长.本题是圆的综合题，考查了切线的性质和判定、三角形的中位线、三角形相似的性质和判定、圆周角定理，第二问设圆的半径为r，根据三角形三角函数和相似列比例式，列方程解决问题.

选题的意义

1.感受圆类几何综合题的基本分析思路，领悟运用执果索因、由因导果分析法帮助解决几何探究题的重要性.

2.经历多题一法或一题多变训练思维、提升解题能力的基本过程.