正确画图直观解题

摘 要：在初中数学课堂上，画图属于非常有效的解题策略之一，画图能够将题目中一些较为复杂的数量关系直接提取出来，由此化繁为简，便于学生迅速理清解题思路.因此在初中数学教学中，教师应当恰当进行画图训练，深入浅出的挖掘教材中的图形资源，使学生能够快速且准确的作图，通过画图来解决数学问题，全面提高学生的综合能力.

关键词：初中数学;画图解题;教学策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）11-0004-02

作者简介：王莉璠（1982.12-），江苏省无锡人，中学一级教师，从事初中数学教学研究.

在初中数学教学中，大部分内容都与图形有关，如函数图像、统计图等，空间与图形部分更是处处有图.在解答问题时，除了读图外，还需要画图.在数学课堂上，教师可引导学生从题目中获取信息，帮助学生合理分析问题，采用丰富的教学方法，合理挖掘题目中的图形资源，对图形进行合理“变身”，如此便能够取得良好的教学效果.

一、通過画图巩固与掌握基础知识

掌握数学基础知识是运用数学知识解决问题的重要前提，学生错解或无法解答的主要问题在于没有正确理解并掌握基础知识.因此在教学中，教师可引导学生在画图的过程中深入理解基础知识，相较于传统的教学方说，此种方式更容易被学生所接受.

例如，在教学“无理数概念”时，教师就可对学生进行引导，如图1，先画出两个边长为1的正方形，将这些图形沿着一条对角线剪开，组成一个大的正方形.

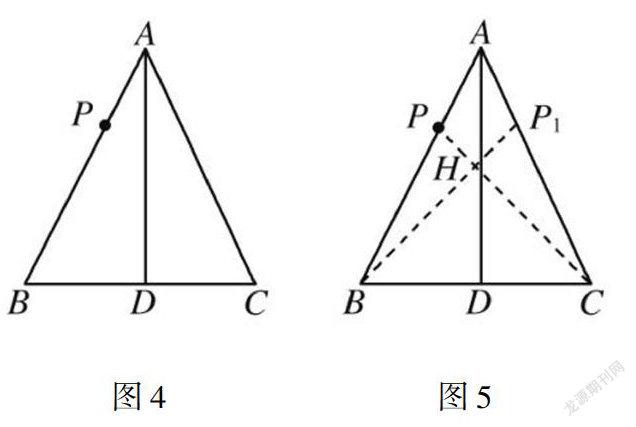
此时教师就可提出问题，对学生进行引导：“大正方形面积是多少？”学生立刻回答：“2”.教师可继续提问：“非常正确，那么假如大正方形的边长为a，那么a2=2，a是有理数吗？”此时学生陷入了思考，教师可对学生进行启发：“想要说明a是不是有数，我们应当先看a是不是能够表达为有限小数或无限循环小数，即分数.”经过教师的启发，学生纷纷开动脑筋，有的学生说：“因为12=1，22=4，因此a是大于1且小于2的数.”有的学生说：“因为32×32=94，因此a不是32.因为43×43=169，53×53=259，因此a也不是43、53…”教师可对学生进行的思路进行肯定，同时继续启发学生：“我们可以量一量图，用量出来的结果，即近似值来算一下.”学生得出了如下结果：“因为”1.5×1.5=2.25，1.4×1.4=1.96，因此1.4

教师肯定了学生的想法后，就可对问题进行拓展：“那么圆周率π也可以借助数轴上的点来体现吗？我们是不是可以借助上面的方法来解答问题？”学生思想考后回答：“我们可先做一个直径为1个单位长度的圆片，周长为π，然后将圆片上的点A放在原点，同时将圆片沿着数轴的正方向滚动一周，点A到达的位置点A’表示的数即为π，如图3.”

最后由教师进行总结：“本堂课我们认识了无理数，通过计算我们认识到了其属于无限不循环小数，而通过画图，我们发现了它的存在形式，还掌握了其在数轴上的表示方法.”无理数的概念较为抽象，通过画图就能够帮助学生更好的体会到它的内涵.可见，通过画图，学生就能够直观并深入的理解数学基础知识，因此在课堂上教师应当把握时机，将数学知识与画图方法结合起来，便可提高课堂的教学质量.

二、分析解题思路绘画图形巩固与掌握了基础知识后，教师就可带领学生进行画图解题训练.初中数学的各个板块，都会涉及到图形内容，因此在课堂上，教师不仅要交给学生灵活的解题思路，同时还需提醒学生通过画图来解决问题，可从以下几方面着手：

第一，带领学生熟悉具体的解题步骤与程序.在具体教学中，教师应当多挑选一些针对性的例题进行示范讲解，重点突出画图解题的便捷性，在教学中，教师可对具体的解题步骤进行分析与总结，经过反复练习，学生自然能够掌握解题的方法，同时也能够体会到画图的作用，从而有效提高学生的解题效率.教师在课堂上可借助创新作图的方法来对学生进行引导，例如在解答与三角形有关的题目时，教师就可带领学生使用彩笔等工具来作图.

例如，在△ABC中，已知AB=AC，AD⊥BC于D点，而图4中P是AB上的任意一点，请你使用无刻度直尺在AC上寻找点P1，使AP=AP1.

解答此类问题的基本思路是将图中的CP连接起来，相交AD于H，同时连接BH并延长交AC于P1，通过说明△ABP1约≌△ACP就能够证明AP=AP1，见图5.

第二，遵循循序渐进的原则，强化学生的画图解题能力.为了有效提升学生的画图解题能力，教师需结合学生的具体情况来调整教学策略，遵循循序渐进的原则，结合学生思维发展水平来进行画图教学.对于七年级的学生来讲，画图解题的目标可适当放低，让学生看懂线段图，同时能够结合线段图来列出算式即可;对于八年级的学生来讲，则可要求学生按照图形来分析应用题的数量关系，学会解决一些实际问题.因为八年级的学生已经有了一定的知识储备，教师可引导学生结合题意画图解题，例如某水库在今年四六月雨季时，水位升高了3m，而到了七月时，水位下降了-4m，那么这4个月以来，水位经历了多少m变化？

图6在教师的引导下，学生通过对数轴图中的数量关系进行分析，顺利得出了答案，水库经历了7m的变化.可见画图解题不仅属于一种必备技能，同时也是观察与实践的过程，在打好基础知识的条件下，教师应当恰当安排画图解题练习，有效提高学生的综合素养.

总而言之，画图对于解决数学问题来说具有非常重要的作用，学生通过画图能够将数学知识简化，使抽象的条件变为学生更容易理解的形象内容.因此在课堂上，教师应当先帮助学生巩固基础知识，开展多样化的教学活动，加强实践，由此提高数学教学的有效性.

参考文献：

[1]明廷军.关注图形平移过程掌握图形变化规律——微课教学的实践探索[J].中学数学研究（华南师范大学版），2020（18）：48-50.

[2]许雯.对初中数学图形等面积拼接问题的教学反思[J].北京教育学院学报（自然科学版），2012，7（04）：54-56+68.

[3]陈德燕.数学核心素养理念下的立体几何教学——以“直线与平面垂直的性质”为例[J].数学通报，2017，56（02）：36-38+44.

[4]王一新.初中数学反思性学习习惯的培养——以几何教学为例[J].科学咨询（教育科研），2020（03）：159.

[责任编辑：李 璟]