基于流量预测的路径选择研究与应用

基金项目：湖南省教育厅科学研究项目《基于云计算的智能交通系统的研究》（课题号：17C0279）

摘要：路径选择技术作为交通诱导系统的核心，近年来已经有了很大的发展。交通道路的路径选择又称车辆行驶路径优化或者最短路径搜索，在实际的交通诱导系统通常转化为图论中的最短路径搜索问题来求解得到。而目前应用在交通路径选择领域的算法主要是 Dijkstra 算法，本文将以 Dijkstra 算法为切入点，在流量预测的基础之上进行路径选择技术的研究。

关键词：路径选择;Dijkstra 算法;路径优化

路径选择在城市道路的交通流分配中最关键的问题之一。对出行者来说，最优化的行驶路线就是最快到达目的地，即行程时间最短或者是行驶的路程距离最短。交通信息具有随机、动态、复杂以及不确定的特性。在海量交通信息中， 快速提取有效信息并高效地反馈给出行者是至关重要， 路径优化算法成为解决问题的关键。本文将在交通流量预测的基础上，对出行者提供准确的最优化行驶路线进行研究，设计基于 Dijkstra算法的路径选择。

一、路径选择

1、路径选择问题描述及分析

（1）路径选择数学描述

路径的选择过程通常要考虑交通道路网络的等级、长度、类别、行程时间等属性数据，在处理交通路网时通常将其作为图论中的“图”。道路的交叉口或者路口的终点即为图论中的结点（Node）;两个结点之间的路段即为图中的边（Edge），带有方向的边称为弧;每条边都有自己的权值，用路段的某些属性特征值来表示。根据这些可以将城市路网抽象化成一个带有权值的图，从而把最优行驶路线问题转化为图论中的寻找最短路径问题。

（2）道路权重的确定

道路权重的值直接关系者路径优化搜索，主要的道路权重有效指标有出行时间、出行的距离、出行费用等。

（3）路径优化处理过程

路径优化的处理过程主要是路网的抽象、確定道路权重的大小、采用合适的搜索算法求解抽象化之后的图中的最短路径、最后得到最优化的行驶路线提供给出行者。

2、路径优化的步骤

路径优化的根本问题是最短路径问题，大多数路径优化问题都可以转化为最短路径问题，由此可知，路径优化的基本步骤与最短路径求解相似，路径优化的一般步骤如下：

（1）对现实的路网进行数据化。路径优化算法处理的是数据信息，因此要首先把实际路网信息转化为算法可以处理的路网信息。

（2）路网权值的适应性转化。由于路径优化的标准不一样，算法处理路网权值的依据也不相同，因此，路网的权值要做一些适应性的改变，把原有的距离权值转换为目标性的权值。如路段行车时间、路段行车花费等。

（3）路径寻优。利用路径优化算法处理路网权值，求解最优路径。

（4）路径还原。将算法求取的最优解转化为实际的路网路径。

二、路径优化算法

1、基于 Dijkstra 算法的路径选择

Dijkstra 算法是由 E.W. Dijkstra于1959 年提出的一种求解带权有向图中从某一源点到其余各点的最短路径的一种有效算法， 能够得到最优解， 该算法针对具有非负权值的图。其主要思想是用逐点增长的方法构造一棵路径树，从而得到从该树的根结点（即指定结点）到其它所有结点的最优路径，时间复杂度为 O（n2）。

该算法的路径选择基本原理是：在已知的带有权值的有向图中，搜索两个已知节点 vo和 vd之间的最短路径。在搜索的过程中，对于任意节点m，标记该节点到起点的距离d（m），称为永久标号或临时标号，求解的过程就是临时标号转化为永久标号的过程，一般将下一可选节点中临时标号d（m）最小的标号转化为永久标号。

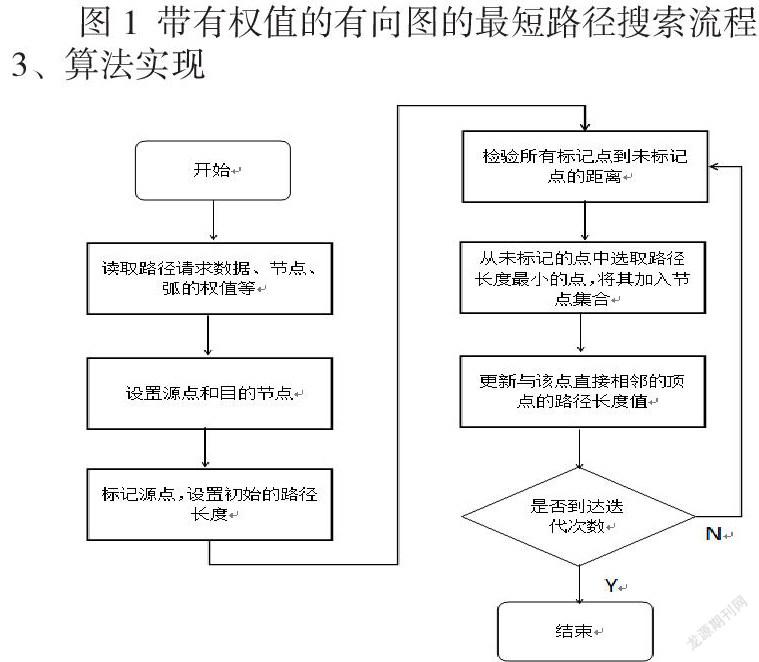
2、算法流程

基于 Dijkstra 算法的带有权值的有向图的最短路径搜索流程如图所示。

3、算法实现

Dijkstra 算法解决的是单元最短路径问题，也就是说图中源点是确定的而另一节点具有任意性。最短路径具有一个特性—最优子结构性质，该性质的描述是：假设P（i，j）={Vi，...，Vk，...，Vs，...，Vj}是从源点 i 到节点 j 的最优化路径，其中 s 和 k 是该最优化路径上的一个中间点，则 P（k，s）必定是从 k 到 s 的最优化路径。

以上图的路网结构为研究对象来实现 Dijkstra 最短路径的计算搜索过程，即对图G=（V， E， W）中节点间的最短路径进行求解，源点为 V0，集合 U={V0}，集合 T 包含除源点之外的所有节点，dist[i]为源点 V0与 i 节点之间的最短距离，path[i]为源点 V0与 i 节点之间的路段上 i 节点前的一个节点，算法的实现过程如下：

（1）从除了源点之外的节点中找出使得 dist[i]值最小节点 i，然后将节点 i 加入到集合 U 中去，此时 U={V0，Vi};

（2）其次，将 Vi作为中间点，修改 T 中各定点的路径长度，更新与 i 直接相邻的节点的 dist 的值。计算公式如下：

（3）重复以上步骤依次将剩余节点加入集合 U 中，直到其包含所有节点，停止迭代。

四、总结

最短路径问题，是图论研究中的一个经典算法问题。Dijkstra算法，是解决最短路径问题的较好算法。本文研究路径优化对象仅仅局限于简化之后的路网模型结构，而实际道路路网结构较为复杂且庞大，对于整个城市路网的路径选择算法还有待进一步的研究。

参考文献：

[1]张轮，杨文臣，张孟.智能交通与智慧城市[J].科学（上海），2014，66（1）：33-36

[2]王树西，吴政学.改进的Dijkstra最短路径算法及其应用研究[J].计算机科学，2012，39（5）：223-228.

[3]王树西，李安渝.Dijkstra算法中的多邻接点与多条最短路径问题[J].计算机科学，2014，41（6）：217-224.

作者简介：王柯（1966—），男，教授，湖南城建职业技术学院，研究方向：计算机应用技术。

湖南城建职业技术学院 湖南 湘潭 411101