大空间建筑环形点式重载作用下深废矿坑岩壁变形稳定性数值分析

仉文岗 吴嘉昊 韩馥柽 何昌杰 李建新 黎泳钦

摘 要：近年来，大城市工程建设急速发展，土地资源愈发紧张，一些矿产资源型城市中出现了利用废弃天然矿坑进行地下空间开发的改造项目。以长沙湘江欢乐城深废矿坑改造开发工程项目为背景，针对矿坑边坡稳定性以及受建筑结构点式荷载作用下的岩壁与基础协同作用问题，利用数值分析手段建立三维岩壁建筑结构相互作用模型。研究岩壁在环形点式受荷条件下的表现，并探究遭遇突发性岩壁变形及承载状态变化后岩壁与结构的稳定性变化情况。结果表明：在天然状况下，废弃矿坑的开采高边坡基本处于稳定状态;而施工扰动和建筑荷载造成的应力变形仅发生于岩壁表面，未达岩体深部;岩壁由于突发灾害产生的局部大变形会严重危及支承其上的基础和结构安全;而在合理的建筑物环形点式基础设计布置情况下，基础结构的偶然失效不会影响岩壁和建筑物的稳定性。

关键词：矿坑;高边坡;环形点式支承;岩壁结构协同作用;边坡稳定性

Abstract： In recent years， with the rapid development of urban construction， land resources are increasingly tense.In some mineral resource-based cities， the transformation projects of underground space development using abandoned natural mining pits have appeared.This paper focuses on the rock slope stability problem with reference to a deep mining pit renovation project in Changsha. Aiming at the stability of mine pit slope and the synergistic action of rock wall and foundation under the point load of building structure， a three-dimensional interaction model of rock wall-building structure has been established by numerical analysis method. The behavior of rock wall under circular point loading has been studied. And the changes of stability of rock wall and structure after sudden deformation of rock wall and change of bearing condition have been also investigated.The results show that the mining high slope of abandoned pit is basically in a stable state under natural condition; the stress and deformation caused by construction disturbance and construction load only occur on the surface of rock wall， not reach the depth of rock mass; local large deformation of rock wall due to paroxysmal failure will seriously endanger the safety of the mining pit foundation and its overlying structures.The occasional failure of the foundation structure will not affect the stability of the rock wall and the building under the reasonable design and layout of the circular point foundation.

Keywords： mining pit; high slope; annular point loading; rock-structure interaction; slope stability

近年来，随着城市化进程的加快以及基建能力的提高，土地资源越来越宝贵。在一些矿产资源型城市中，出现了填埋废弃矿坑进行空间开发的研究和项目，根据矿坑的具体特点，因地制宜地加以改造，将其再利用，作为博物馆、娱乐场、风景区等用于旅游商业开发。

在深废矿坑中进行改造再利用施工对既有矿坑岩壁稳定性的影响是一个极为重要的问题[1]。针对该问题，学者们已从多角度采用多手段探索岩质边坡的工程受荷行为，并評估其变形稳定性[2-4]。此外，通过对岩质边坡受桥基荷载的研究分析发现：在一定区域内由单一桩基传递到岩壁的荷载都可以近似成点式荷载[5-6]。当岩质边坡作为上部建筑主体的承载对象时，为保证边坡及上部结构稳定性，应整体考虑岩壁与支承于其上的结构基础相互作用协调变形的过程[7-8]。然而，使用解析方法分析边坡和桩基础力学行为的研究往往以力或位移的形式简化代替边坡与结构体的相互作用[5-6，9-10]，可能造成对结构与岩体受力变形情况和破坏机制预测的不准确。采用试验和数值手段对岩质边坡受结构荷载行为进行分析时，学者们通常只针对单个桥台桥墩存在的情况进行模拟[11-14]，故考虑多点受荷情况以及荷载分布形式是查明岩质边坡受荷表现的重要条件。针对已有研究存在的问题，笔者以环形点式受荷条件下废弃矿坑高边坡为研究对象，探究其三维空间稳定性问题以及岩壁与结构协同作用变形机理。基于湖南湘江欢乐城深废矿坑再利用工程，针对在天然矿坑内进行施工活动过程中涉及的岩质边坡稳定性问题，以及在环形点式受荷条件下的岩壁与基础相互作用、协同变形问题，采用PLAXIS软件对岩壁点式环形支承的大空间建筑与深废矿坑岩壁协同作用进行了三维有限元建模分析。

1 工程概况

湘江欢乐城深废矿坑商业改造工程位于长沙市岳麓区坪塘镇山塘村狮峰山村地段。该场地是历时50多年开采后遗留的深大矿坑，整体长约440 m、宽350 m，地形地质复杂，场地情况如图1所示。

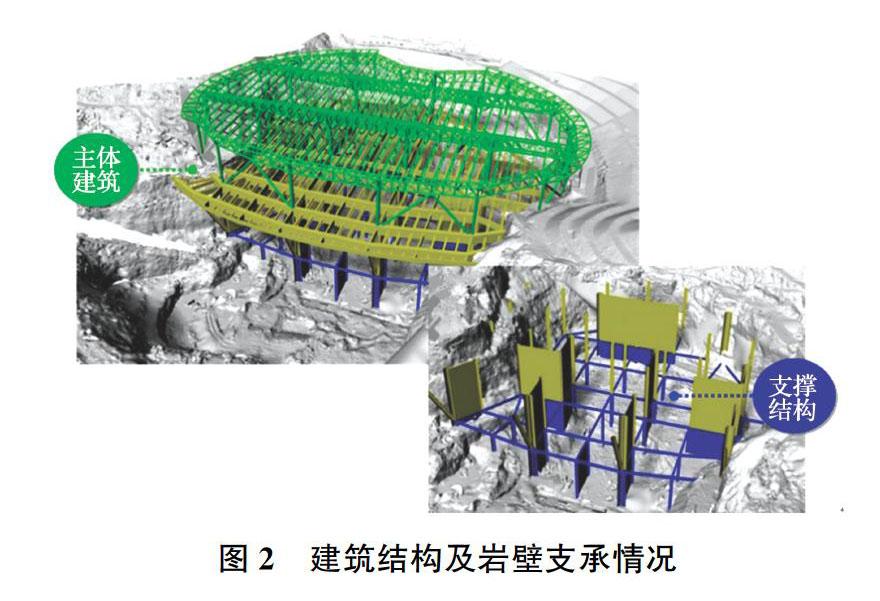
矿坑平面可近似为两个尺寸不同的椭圆，主体建筑结构集中在北侧深坑，通过墩柱结构支承于矿坑各级岩壁之上，矩形排列的柱结构通过横梁连接，如图2所示。场地存在矿坑开采高边坡，主要为岩质边坡，拟建物距坑壁最近距离为5～10 m。坑壁边坡高40～50 m，坡度80°左右。

1.1 地质构造及水文条件

拟建场地无全新世活动断裂，可不考虑断裂对场地的稳定性影响。场地存在多级不规则边坡，经雨水冲刷、掏空，边坡多处出现小范围坍塌现象，但现状整体基本稳定。建筑主体结构施工时，应采取必要措施对高边坡进行支护处理。

场地深度范围内地下水主要为上层滞水及基岩裂隙水。上层滞水分布于场地的人工填土中，稳定的水位埋深在5.00～6.10 m之間，水量较小;基岩裂隙水存在于场地基岩灰岩中。两者水力联系相通，无稳定隔水层。

上层滞水对混凝土结构具微腐蚀、对混凝土结构中的钢筋具微腐蚀。据勘测结果，主体结构场地范围内未发现溶洞，局部有溶蚀现象，故不考虑岩溶空洞影响。

1.2 地层岩性

场地主要岩土层分布为：杂填土①（①为地层代号，下同）结构松散～稍密状，场地内广泛分布，平均厚度7.81 m;粉质黏土④一般为硬塑状，局部可塑状，场地内局部分布，平均厚度8.21 m;岩层主要为完整性程度较破碎～破碎的微风化灰岩⑨-3，为裂隙块状或中厚层状构造，属较硬岩，岩体基本质量等级为Ⅳ级，其下分布有微风化灰岩⑨（Dq），厚层状构造，属坚硬岩，岩体基本质量等级为Ⅲ级，岩石质量指标（RQD=75～90））较好，该层为场地基岩。

2 数值模型建立

针对湘江欢乐城项目深废矿坑商业开发建设过程中的岩壁及结构稳定性问题，采用PLAXIS软件对场地岩土体及结构基础进行三维有限元建模分析。主体区域下卧矿坑平面几何形态近似长轴240 m、短轴160 m的椭圆形，为简化建模，将不规则的矿坑平面形态近似成多个折线段开展数值模拟，并假设经工程壁面处理后的坑底为平面;将主体建筑下卧区域假定为相同的坡面形态，4级放坡，如图4（a）所示。模型尺寸500 m×500 m×80 m（x-y-z轴）。

为简化数值模型，建模时考虑各层岩土体为近似水平分布，粉质黏土层主要分布于场地建筑主体结构西南侧，故建模时考虑粉质黏土层由模型边界向模型中部逐渐尖灭;场地地层建模情况与主要参数见图3和图4。采用四面体单元对岩土体进行模拟，该种类型的网格单元可适应并模拟复杂的几何模型[15]。

由于有限元软件内部未区分土与岩的材料差异，只能采用本构模型与物理力学参数对岩土层的性质进行定义和划分。但限于计算效率和节理面信息缺失，对灰岩层进行建模时未考虑节理面的存在，故数值模拟中的岩体各向同性。模型结构构件主要包括：矿坑坡面与底面进行岩壁处理施作面板、上部建筑主体底面（将上部建筑结构简化为承载竖向荷载的建筑底板）、传力柱以及下部连接的基础、连接柱的梁。结构的模拟情况见表1。

对矿坑岩壁稳定性分析模型施工步骤共考虑建立9个分阶段，如表2所示。岩壁与结构协同分析模型在上述稳定性分析基础上，增设岩壁或结构受力变形突变的计算步骤，如表2中最后一步。

3 矿坑岩壁稳定性分析

3.1 自然状态下矿坑岩壁蠕变

图5是经过长期变形稳定后的矿坑变形云图（俯视图）。在无工程施工的情况下，矿坑坡面及坑周土体变形值保持在较低水平。变形基本发生在上部杂填土和粉质黏土层内，即第1层放坡面位置处。浅层软弱土体受卸荷作用影响，产生12.62 mm的变形，且以向上的隆起为主，坡度较缓的斜坡面产生了少量的侧向位移。深部岩体力学性质好，卸荷、蠕变产生的变形可忽略。

3.2 施工扰动下矿坑岩壁变形

矿坑坡面在结构施工扰动的情况下，位移主要发生在性质较差的填土或黏土层中的结构接触位置，且以沉降和面向岩体的压缩变形为主，坡顶位置产生少量隆起和向临空面的位移;岩体在受荷作用下发生的变形量可忽略。

上部均布荷载由0 kN/m2逐步增大至80 kN/m2，以模拟建筑主体结构施作，岩土体最大位移由19.31 mm增大至34.98 mm。此外，随着柱、基础传递的竖向荷载值逐渐增大，土体位移水平分量占比逐渐减小，杂填土（及粉质黏土）层中土体位移形式逐渐转变以沉降为主。

4 岩壁与结构协同作用分析

在矿坑自然状态及结构正常运营状态变形稳定性分析的基础上，本章节针对两个基本问题进行分析：环形点式岩壁支承建筑荷载变化及局部岩壁大变形引起的岩壁、结构安全性问题;支承于岩壁上的柱基础发生突发性破坏时，岩壁及周边结构的响应情况。

4.1 局部结构超载作用

对上台阶局部施加变荷载，以探索位于杂填土层（或粉质黏土层）中的上台阶承受过大结构荷载会对周围岩体、结构产生怎样的受力变形影响。大范围区域内施加恒定的竖向均布荷载40 kN/m2，随后上台阶以及地表局部位置承受由柱和基础传递的竖向荷载由40 kN/m2逐渐增大至160 kN/m2。

当杂填土中的上台阶基础承受由柱传来的160 kN/m2的竖向荷载并传递至岩壁时，根据图6岩土体位移矢量图可以看出，第1级放坡台阶处的杂填土受重荷发生了大幅度下沉，最大值58.5 mm，而坡顶放坡位置发生小幅度侧向位移11.3 mm。下部各级台阶承重处产生的受压沉降基本可控。

图7是在局部荷载变化过程中支撑于各级台阶上的柱结构所产生的最大变形值变化情况。变荷载施加在第1级台阶柱上，由于采用的是线弹性结构单元模拟传力柱，故初台阶柱体变形值随竖向荷载线性增长，且最大值皆发生在柱顶。由上台阶承受的局部大荷载，传递到了第2级台阶处，造成了该台阶的岩壁以及支撑于其上的基础与柱结构变形值有所增大。而第3级台阶和坑底结构基本不受上部台阶荷载的影响，只于直接施加在其上的建筑荷载相关。

4.2 岩壁突发大变形作用

4.2.1 初台阶局部下沉

为研究岩体变形情况对结构应力应变的影响，通过对杂填土层（或粉质黏土层）中局部上台阶施加面位移，模拟局部的台阶由于过大荷载产生较大变形下沉，探索此过程中局部区域内结构的受力变形变化情况。

初台阶局部下沉引起的周围基础柱体结构受力和变形差异见图8，在发生局部大变形前，岩壁在承受环形点式荷载的作用下，支承于各级台阶上的柱结构变形分布较为平均，均在15～25 mm之间;发生局部大变形之后，支承在局部初台阶以及相邻两级台阶上的柱体发生的位移大幅增长，涨幅最大达到了247%，而分布于坑底和第3层台阶上的基础柱体未受到较大的影响。图8（b）是对应的轴力最大值绝对值对比，结论与变形结果相似，下沉的台阶与相邻台阶上的结构受影响程度较大，且轴力急剧增长至387.7×103kN。在实际工程中，工程结构材料非线性，过大轴力值可能会导致结构体进入屈服甚至屈服后状态，造成区域内多个柱结构失效。故杂填土或粉質黏土层若发生大变形，可能会对基础以及支承结构的稳定性造成严重不良影响。

4.2.2 斜坡面法向位移

对第2级放坡侧壁施加法向位移，模拟岩体表面突发垮塌破坏对岩壁和结构稳定性的影响。面位移情况如图9所示。局部变形之前，岩土体中产生的最大位移为31.8 mm，且集中在第1层台阶支承基础的位置。施加局部斜向位移后，岩壁最大位移增大至56 mm（减去了施加的位移），典型剖面的变形矢量如图9所示。上部两台阶以及斜向坡范围内的岩壁表面受卸荷作用，发生向临空面的大幅变形，但并未发展到岩体内部位置，第3级台阶和坑底岩体所受影响较小。

局部岩壁的侧向位移对支承在各级台阶上的基础和柱结构的变形存在较大的影响。岩壁受卸荷作用向临空面发生变形，使得其上的柱体变形形式由沉降为主转变为侧向为主。图10展示了第3级台阶上的柱体在施加局部位移前后的变形情况。在正常承载工况下，柱体发生少量下沉位移，侧向变形发生在柱身下部，而在岩壁面发生突然的侧移后，各级台阶表面岩体都发生了不同程度的隆起和斜向变形，因此造成了其上的结构构件发生相似的变形：柱体发生上移，并且侧移量相较之前增幅极大。柱体顶部往往考虑归结于上部结构底面，下端产生较大的侧向位移会在柱体内部产生较大的剪力和弯矩，可能会对结构稳定性造成危害。故岩壁斜坡若发生较大的侧向位移，可能会对支承结构以及上部建筑主体的稳定性造成严重不良影响。

4.3 单柱失效荷载传递机制

针对不同台阶处的单个传力柱结构失效，以模拟施工意外或过大荷载造成的单柱失效，探究荷载向周围梁、柱的传递机制。

根据计算结果，单个柱体的失效，造成梁结构的局部悬空，该位置的下沉量由30.92 mm急剧增大至178.4 mm，如图11（a）所示。支承情况的变化也造成了梁的内力变化，图11（b）是柱失效前后的梁弯矩图，弯矩分布形式发生了明显变化，其数值也增长至5倍。梁变形和受力大幅增长，可能会造成混凝土开裂，影响梁的承载效果。

单柱失效后，其上原本的竖向荷载通过梁和主体结构底板转移到其他柱体。通过分析发现，支承在杂填土和粉质黏土层中的柱体承受的荷载远小于支承与岩体上的柱体承受的荷载，故其失效造成周围柱体荷载增量可忽略不计;而支承与岩壁上的柱失效后，会造成周围各柱的承载情况发生不同程度的增加。表4列出了支承于第2层台阶岩壁的单柱失效后，周围柱体的轴力变化情况。下部岩壁上的各单桩失效情况与此相似。

由表4结果可知，单个基础或传递上部结构荷载的桩体失效，主要会对连接于其上的横向和纵向梁产生较大的内力、变形增量。支承在岩壁上的单桩失效后，其原本承受的荷载会转移到周围其他桩，造成周围桩体内的轴力值增大，但增幅不大，不会造成渐进式的连续桩体破坏。

5 结论

以湘江欢乐城项目中的深废矿坑再利用开发工程为例，通过数值模拟手段，对天然矿坑岩壁在点式环向受荷条件下岩壁的稳定性问题以及岩壁与结构协同作用问题开展了深入研究，得到以下主要结论：

1）在天然状态以及结构正常运营桩体下，矿坑岩壁产生的变形量基本可控且仅发生在靠近临空面的表层土中。

2）局部结构超载会导致邻近岩壁与基础的下沉增量，但对深部岩体影响甚微。

3）岩壁由于突发灾害产生的局部大变形，会对邻近部位的基础以及支承结构稳定性造成不良影响，严重者可致区域性的结构失效，从而影响上部主体结构的安全运营。

4）单个基础或传递结构荷载的桩体失效后，荷载大量传递至其上连接的梁结构，可能导致梁结构局部开裂甚至逐渐发展为断裂失效。但转移到周围其他桩的荷载有限，不会造成渐进的连续桩体破坏。

参考文献：

[1] 师文豪， 杨天鸿， 王培涛， 等. 露天矿边坡岩体稳定性各向异性分析方法及工程应用[J]. 岩土工程学报， 2014， 36（10）： 1924-1933.

SHI W H， YANG T H， WANG P T， et al. Anisotropy analysis method for stability of open-pit slope rock mass and its application [J]. Chinese Journal of Geotechnical Engineering， 2014， 36（10）： 1924-1933. （in Chinese）

[2] 张海娜， 陈从新， 郑允， 等. 坡顶荷载作用下岩质边坡弯曲倾倒破坏分析[J]. 岩土力学， 2019， 40（8）： 2938-2946，2955.

ZHANG H N， CHEN C X， ZHENG Y， et al. Analysis of flexural toppling failure of rock slopes subjected to the load applied on the top [J]. Rock and Soil Mechanics， 2019， 40（8）： 2938-2946，2955. （in Chinese）

[3] 代仲海， 胡再强， 尹小濤， 等. 工程荷载作用下缓倾角反倾似层状岩质边坡变形稳定性分析[J]. 岩土力学， 2018， 39（Sup1）： 412-418，424.

DAI Z H， HU Z Q， YIN X T， et al. Deformation stability analysis of gentle reverse inclined layer-like rock slope under engineering load [J]. Rock and Soil Mechanics， 2018， 39（Sup1）： 412-418，424. （in Chinese）

[4] 徐鹏，尚念林，鲍晶晶，等.极限分析法求解含软弱夹层边坡稳定性[J/OL].西南交通大学学报. https：//kns.cnki.net/kcms/detail/51.1277.u.20200915.1638.024.html.

XU P， SHANG N L， BAO J J， et al. Stability analysis of slopes with weak layers using limit analysis method [J/OL]. Journal of Southwest Jiaotong University. https：//kns.cnki.net/kcms/detail/51.1277.u.20200915.1638.024.html. （in Chinese）

[5] 张雷， 王孟渝， 叶勇， 等. 考虑桥基荷载的岩质边坡稳定性数值模拟研究[J]. 地下空间与工程学报， 2009， 5（Sup1）： 1331-1335.

ZHANG L， WANG M Y， YE Y， et al. Numerical simulation research of rock slope stability considering bridge foundation load [J]. Chinese Journal of Underground Space and Engineering， 2009， 5（Sup1）： 1331-1335. （in Chinese）

[6] 赵明华， 尹平保， 张永杰， 等. 高陡斜坡段桩柱式桥墩基础设计计算方法研究[J]. 工程力学， 2013， 30（3）： 106-111.

ZHAO M H， YIN P B， ZHANG Y J， et al. The design and calculation method of pile-column bridge pier foundation in high and steep slope [J]. Engineering Mechanics， 2013， 30（3）： 106-111. （in Chinese）

[7] 王华. 桥基岸坡变形破坏机制物理模拟研究[J]. 岩土力学， 2011， 32（7）： 2034-2038.

WANG H. Study of deformation and failure mechanism of bridge foundation slope with physical simulation method [J]. Rock and Soil Mechanics， 2011， 32（7）： 2034-2038. （in Chinese）

[8] ZOU Z Y， LEI D， JIANG G L， et al. Experimental study of bridge foundation reinforced with front and back rows of anti-slide piles on gravel soil slope under Centro waves [J]. Applied Sciences， 2020， 10（9）： 3108.

[9] 冷涛， 年夫喜. 卸荷裂隙岩体在桥基荷载作用下的力学行为研究[J]. 水利与建筑工程学报， 2016， 14（4）： 173-176.

LENG T， NIAN F X. Mechanical behavior of rock mass near unloading crack under load [J]. Journal of Water Resources and Architectural Engineering， 2016， 14（4）： 173-176. （in Chinese）

[10] 董捷， 宋绪国. 一种考虑桥基附加荷载的斜坡稳定分析方法[J]. 铁道工程学报， 2016， 33（6）： 66-71.

DONG J， SONG X G. Analysis method for the stability of slope considering bridge foundation additional load [J].Journal of Railway Engineering Society， 2016， 33（6）： 66-71. （in Chinese）

[11] 李忠庚， 徐金明， 吴红斌. 桥梁工程施工及运营对岩体边坡稳定性的数值分析[J]. 上海大学学报（自然科学版）， 2014， 20（5）： 596-604.

LI Z G， XU J M， WU H B. Influences of bridge construction on stability of cutting slope using numerical simulation [J]. Journal of Shanghai University （Natural Science Edition）， 2014， 20（5）： 596-604. （in Chinese）

[12] 刘克玲， 王春雷. 桥基荷载作用下角型高边坡临界滑动面研究[J]. 岩土工程学报， 2013， 35（Sup2）： 415-421.

LIU K L， WANG C L. Critical slip surface of high-steep slopes based on theory of stress effect coefficient [J]. Chinese Journal of Geotechnical Engineering， 2013， 35（Sup2）： 415-421. （in Chinese）

[13] FU Z D， JIANG G L， YUAN S Y， et al. Lateral behavior of piled bridge foundation and stabilizing piles on steep slope [J]. KSCE Journal of Civil Engineering， 2019， 23（10）： 4223-4236.

[14] 赵明华， 陈耀浩， 杨超炜， 等. 基于有限杆单元法的陡坡基桩非线性分析[J]. 岩土力学， 2018， 39（8）： 3020-3028.

ZHAO M H， CHEN Y H， YANG C W， et al. Nonlinear analysis of pile in steep slope based on finite bar element method [J]. Rock and Soil Mechanics， 2018， 39（8）： 3020-3028. （in Chinese）

[15] PANAGOULIAS S， BRINKGREVE R B J， ZAMPICH L， et al. To manual [M]. Plaxis bv， Delft， the Netherlands， 2018.

（编辑 胡玲）