锈蚀表面形貌及其对钢材超低周疲劳性能的影响

宋方远 谢旭 张婷婷

摘 要：锈蚀是钢桥耐久性退化的主要形式之一，而锈蚀钢材的表面形貌是改变结构应变分布进而影响超低周疲劳性能的重要因素。为了研究钢材锈蚀形貌及其对超低周疲劳性能的影响，以中国钢桥建设中常用的Q345钢材为例，对4组不同锈蚀程度的人工加速锈蚀钢板试样进行表面形貌测量，讨论了用粗糙度、分形维数和功率谱密度函数3种指标表征锈蚀形貌的可能性;根据三维形貌实测数据建立试样的规整六面体单元模型，并利用循环空穴扩张模型（CVGM）计算了锈蚀钢材的超低周疲劳开裂寿命，分析了锈蚀形貌对钢材超低周疲劳开裂寿命的影响。结果表明：人工加速锈蚀试验的锈蚀速率受锈层阻隔影响明显;对于不同锈蚀时长的试样，各组表面轮廓的粗糙度、分形维数和功率谱密度函数区分度不高;锈蚀形貌的不均匀程度是引起试样超低周疲劳性能下降的重要因素，蚀坑位置的超低周疲劳开裂寿命受蚀坑所处截面缩小程度、所处位置以及形状特征等不均匀因素耦合影响。

关键词：钢桥抗震;蚀坑;钢材锈蚀;超低周疲劳;有限元建模

Abstract： Corrosion is one of the most typical form of durability degradation of steel bridge and the corrosion morphology takes significant effect on the strain distribution of the structural surface，which has evident effect on the ultra-low cycle fatigue performance of steel plate. In order to investigate the characteristics of steel corrosion morphology as well as the effect of the corrosion on the structural ultra-low cycle fatigue（ULCF） performance， this paper takes the steel kind of Q345 as the study case， conducting surface morphology measurements of four groups of artificially accelerated corroded steel plate sampleswith different corrosion degrees.The possibility of characterizing the corrosion morphology by roughness， fractal dimension and power spectral density function is discussed.Meanwhile， precise finite element models consistedby hexahedron elements of corroded specimens are established on the basis of 3D profile data， the ULCF cracking life of corroded steel is calculated using the improved cyclic void growth model （CVGM），and the effect of corroded surface morphology on ULCF cracking life of steel is analyzed.The research results indicate that： the corrosion rates of the artificial acceleration corrosion tests are significantly affected by the thickness of the rust layers.However， the surface roughness， fractal dimension， and power spectrum density function are unable to differentiate the corrosion degree.According to the numerical calculation results， the unevenness of corrosion morphology is the very important factor on the UCLF performance degradation.Also， the reduction of the cross section， the position on the surface of specimens， and the dimension characters of the critical corruption pits contribute a coupling effect on the ULCF cracking life of the corroded steel specimens.

Keywords： seismic design of steel bridge; corrosion pit; steel corrosion; ultra-low cycle fatigue （ULCF）; finite element modeling

在1994年美國北岭地震[1]和1995年日本阪神地震[2]中，不少钢结构在梁柱节点或桥墩底板连接位置发生了超低周疲劳破坏。与破坏性质为脆性断裂或伪脆性的高周疲劳和低周疲劳不同，超低周疲劳的破坏机理是钢材局部塑性大应变引起材料延性开裂，破坏性质为延性断裂，疲劳寿命一般在20周以内[3]。而锈蚀是钢结构耐久性退化的一种主要形式[4-6]，钢材锈蚀不但使结构的截面厚度减小、承载能力降低，而且还会因为表面产生蚀坑引起应力和应变集中，降低结构的延性和疲劳寿命，影响服役钢结构的抗震性能。

迄今，虽然一些学者研究了锈蚀线材的疲劳性能，如Apostolopoulos[7]、Hawileh等[8]研究了锈蚀钢筋在循环荷载下的力学性能;李晓章等[9]、郑祥隆等[10]对锈蚀高强度钢丝的高周疲劳性能进行了试验研究，这些研究均验证了蚀坑位置会加速萌生疲劳裂纹，导致钢筋或钢丝的疲劳寿命显著下降。笔者根据锈蚀钢板的低周疲劳试验结果[11]，发现锈蚀钢板的滞回曲线形状与未锈蚀试样基本一致，而疲劳寿命较未锈蚀试样有明显的下降，且蚀坑是促进低周疲劳裂纹萌生、缩短疲劳寿命的主要影响因素。这表明锈蚀形貌对钢板的低周疲劳强度有不可忽视的影响。为了评价钢板的锈蚀形貌，孔德英等[12]采用图像扫描方法获取碳钢实海挂片的表面形貌并进行分析，建立了扫描灰度值分布与试片局部锈蚀平均深度之间的关系模型;徐善华、王皓等[13-15]研究了锈蚀率与粗糙度、分形维数、蚀坑平均深度之间的关系，并通过逆向建模方法建立了考虑钢板表面形貌的有限元模型，分析了锈蚀钢板的疲劳缺口系数和力学性能。但是，目前关于锈蚀钢板的疲劳研究大多限于高周或低周疲劳范围内，而以延性开裂为特征的超低周疲劳破坏机理与高周或低周疲劳有较大差异[16];锈蚀钢材的超低周疲劳研究十分缺乏，锈蚀在役钢结构的抗震性能评价缺乏依据。

为研究锈蚀钢板的表面形貌特征及其对锈蚀钢材超低周疲劳寿命的影响，为锈蚀在役钢结构抗震性能评价提供依据，笔者通过人工加速锈蚀的方法获得4组不同锈蚀程度的试样，根据实测的表面形貌讨论蚀坑凹凸特征的表征方法，利用扫描得到的锈蚀钢板试样外形建立考虑表面形貌的有限元模型，用循环空穴扩张模型分析表面形貌对锈蚀试样超低周疲劳性能的影响。

1 钢板试样人工锈蚀

由于中性盐雾加速锈蚀结果与自然锈蚀较相近[17]，选用中性盐雾加速锈蚀方法对试样进行加速腐蚀，缩短钢材锈蚀周期。

试验材料为Q345钢，其中弹性模量为204 GPa，屈服强度为386 MPa，极限强度为529 MPa，伸长率为0.40。试件尺寸如图1所示。

试样加速腐蚀装置如图2所示。用立方形塑料罩的简易腐蚀箱，内置镂空试样安放架，在安放架四角的柱子上设置16个定时定量喷洒盐雾的喷头。盐雾为质量分数为5%的氯化钠溶液。

试样在腐蚀前进行称重，然后摆放在试样安放架，经过一定时间锈蚀后，置入酸洗溶液中浸泡10 min左右除锈，酸洗浸泡后用软刷清除表面残留锈蚀产物，并用氢氧化钙溶液中和残余酸液，最后用清水清洗并烘干。称取每个试样锈蚀后重量，并计算得到试样质量损失率，以反映锈蚀程度。

锈蚀试样共64枚，分为4组，每组16枚，标记为X01～X16（X为A、B、C或D）。试样锈蚀时间分别为A组60 d、B组120 d、C组180 d与D组240 d。锈蚀质量损失率数据如图3所示，各组平均质量损失率分别为7.24%、9.61%、9.79%与10.59%。在锈蚀初期，锈蚀速率较高，质量减小明显;经过一段时间后，锈层增厚，阻隔了内部金属与氧化物接触，锈蚀速率减缓，几乎停滞;在锈蚀后期，由于锈层逐渐脱落，锈蚀速率小幅回升。从各组质量损失率的结果来看，除了A组锈蚀程度较小，其他3组锈蚀程度接近。

2 锈蚀表面形貌测量及分析

为了描述锈蚀钢板表面宏观形貌，使用微距照相机与显微镜拍摄钢板表面。作为一例，图4给出人工锈蚀60、240 d的钢板形貌对比。从图4中可知锈蚀试样表面均存在大量不平的锈蚀痕迹，有不少明显的蚀坑。锈蚀时间短的试样表面蚀坑数量少，且分布零星，如图4（a）所示;锈蚀时间长的试样由于蚀坑过于密集，形成蚀坑集落，并在集落内又生成新的蚀坑，表面有较大面积的溃疡状锈斑，如图4（b）所示。

为了获得试样表面的三维轮廓，用思看激光扫描仪PRINCE775对试样进行扫描。图5为实际形貌与三维扫描结果对比。根据扫描结果可见，锈蚀后试样试验段满布位置随机且大小不一的蚀坑，其中最大的单蚀坑深度约为0.7 mm，直径约为3.5 mm。与实际形貌对比可以看出，三维扫描能够捕捉明显蚀坑分布。不难看到，随着锈蚀时间的增加，虽然锈斑面积增大，但并不意味钢板表面单蚀坑会变得深径比更大，或是显得更加明显。

为了获取试样表面详细的不平整特征，如图6（a）所示，在每个试样表面任意选择3道线用布鲁克Dektak XT探针式轮廓仪扫描，得到如图6（b）所示的表面二维轮廓线。

为了评价锈蚀试样表面的凹凸不平程度，这里用粗糙度、分形维数和功率谱密度函数这3种常用的表征参数进行分析。

粗糙度是指表面具有小间距和微小峰谷的不平度，属于微观几何形状误差，粗糙度越大，表面越不平整。粗糙度的主要参量为轮廓算术平均偏差Ra、轮廓均方根偏差Rq和轮廓最大高度Rz。Ra为取样长度内轮廓偏距Z的算术平均值，Rq为取样长度内轮廓偏距Z的均方根值，Rz为取样长度内5个最大轮廓峰高的均值Zp与5个最大轮廓谷深的均值Zv之和，如式（1）～式（3）所示。

图7为4组不同锈蚀时长的试样表面二维轮廓的粗糙度统计图。由图7可知，随着锈蚀时长的增加，3种粗糙度均呈先增大后减小的趋势，且变化量较小。

分形是Mandelbrot[18]提出并创立用来描述自然界具有自相似性的不规则形态的一种数学理论。分形维数是用来定量描述分形几何的自相似性特征的参数，通常可由计盒数法得到[19]，如式（4）所示。

图8为各组试样表面轮廓分形维数的统计图。不同锈蚀时长各组试样表面轮廓的分形维数十分接近，且均值都在1.03～1.04之间，表明锈蚀时长达60 d以上的试样锈蚀表面分形维数区分度不高。

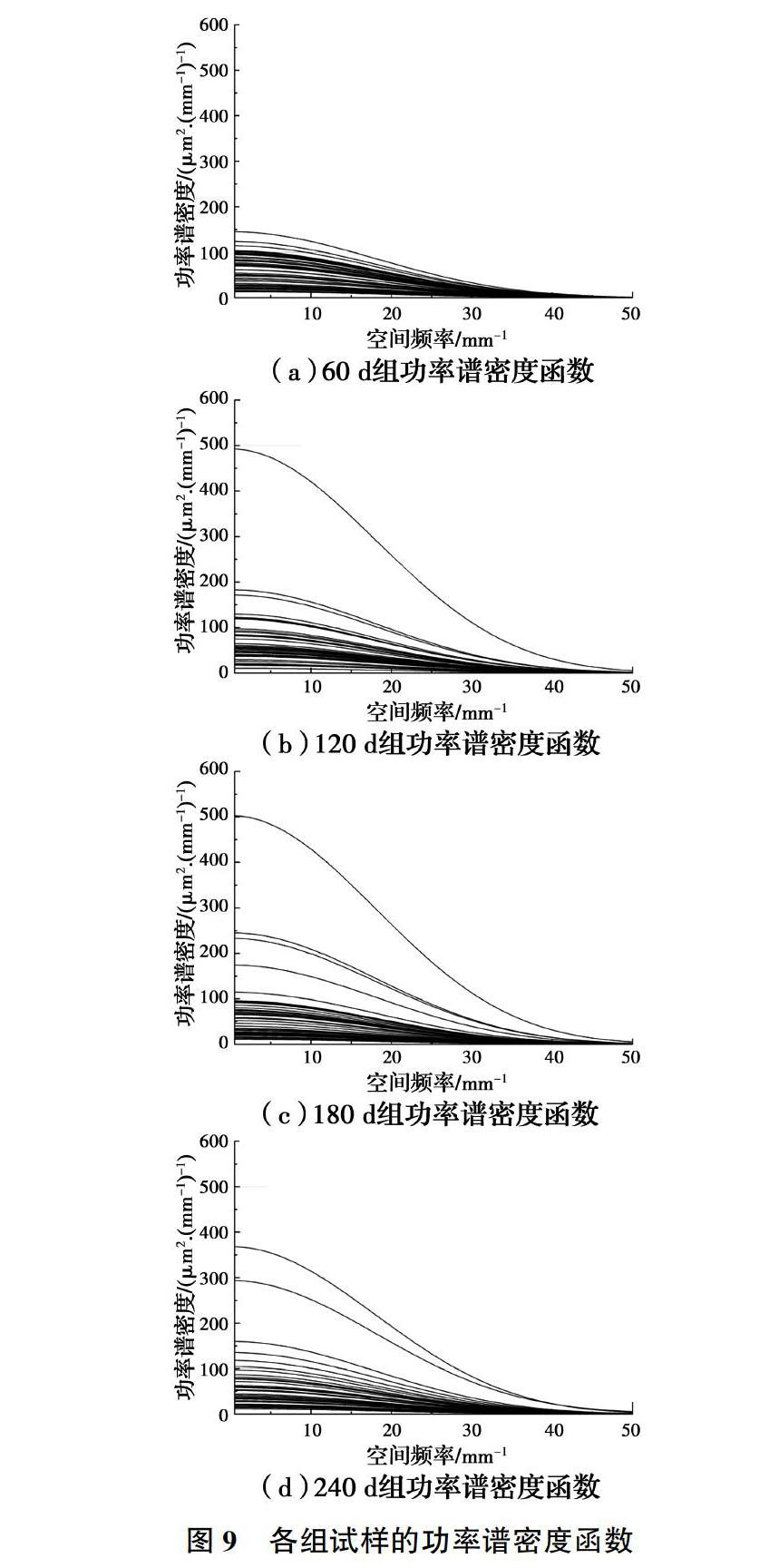
功率谱密度函数是信号在频域内的有限均方值。锈蚀表面形貌是描述空间域中的信号特征，因此横坐标采用空间频率，指单位长度（1 mm）内包含的形貌波形的波数。分析轮廓在空间频域内的功率分布情况，可为比较不同试样的锈蚀程度提供依据。图9为其中各组试样表面轮廓功率谱密度函数统计图。对比可知，大多数轮廓曲线的功率谱密度峰值在150以下，只有极个別轮廓曲线峰值较高，表明功率谱密度函数用于描述锈蚀表面形貌效果不理想。

通过对粗糙度、分形维数和功率谱密度函数的对比分析可以看出，尽管微距照片、3D扫描显示不同锈蚀时长下试样表面锈蚀形貌有很大区别，但各个锈蚀形貌表征参数并没有表现出显著的差异。试验中共采集分析了192条轮廓线，二维轮廓扫描只能反映极其有限的表面形貌特征。本次扫描的4组不同锈蚀时长的试样中，锈蚀质量损失率差异并不十分显著，尤其时长达到120 d及以上的锈蚀损失率，因此，上述锈蚀形貌表征参数评价试样表面锈蚀程度的适用性有待验证。

3 考虑表面形貌影响的锈蚀钢材超低周疲劳性能分析

3.1 超低周疲劳破坏判据

超低周疲劳破坏是钢桥在地震作用下最有代表性的破坏形式之一。1995年日本阪神地震以后，多国学者们对钢结构超低周疲劳的机理和算法进行了大量研究。目前，主要有两类验算方法，一是基于Coffin-Manson公式的经验方法，二是基于微观损伤机制的半经验、半理论方法。尽管Coffin-Manson公式得到了一系列改进，但这类方法不能考虑应力三轴度的影响。第二类方法主要有循环空穴扩张模型（cyclic void growth model， CVGM）和连续损伤力学模型（continuum damage model， CDM）两种模型。其中，CVGM模型是Kanvinde等[20]基于Rice-Tracey的空穴半径增长公式提出的预测模型，该模型将超低周疲劳破坏的临界状态定义为

式中：等式左边为循环荷载下的材料空穴增长指标，右边为临界空穴增长指标;T为应力三轴度;εaccp为受拉循环开始时的累积等效塑性应变;dεtp与dεcp分别为拉伸与压缩循环中的等效塑性应变增量;λ为材料损伤退化参数;η表示单调拉伸时的材料韧性参数。

Li等[21]在此基础上改进了CVGM，将断裂判据按预测位置的平均应力三轴度高低分为两种情况讨论，对于高应力三轴度情况（T>0.70），Q345钢材的损伤退化参数λ=-0.08;对于中应力三轴度情况（0.33

3.2 有限元模型

为了分析锈蚀对钢材超低周疲寿命的影响，利用扫描得到的三维形貌数据建立考虑锈蚀影响的精细有限元模型，并用CVGM模型进行分析。为此，使用逆向工程软件Geomagic Studio将扫描得到的IGS点云数据转化为三角形网格构成的STL格式数据，进而建模生成实体模型。但是直接生成的四面体网格单元在考虑复杂工况的有限元计算中精度较差，笔者利用HyperMesh中的Morph模块将规则的点阵覆盖到三维扫描模型表面，再借用其网格编辑功能构建出规则的、适用于超低周疲劳计算的六面体单元模型。上述建模方法的具体步骤如下：

1）扫描得到的原始数据存在一定缺陷，如空洞、毛刺等。数据导入到Geomagic Studio后需删去产生毛刺的多余点，补完产生空洞的区域，修整扫描模型，方便后续操作，如图10所示。

2）如图11所示，将修整模型导入HyperMesh，选择试样中间长度为30 mm的试验段上下表面作为后续mapping操作的目标面，删去其他多余的单元，记为T1与T2;然后新建两个规则网格，大小需要尽量覆盖但不超出目标面，记为M和N。调整4个面的位置，使各个面的中心法线大致重合。

3）使用工具栏中HyperMorph下的map to geom功能，3个选项栏分别设置为“map to elements”、“map nodes”和“along vector”，选择映射节点（M）与映射目标（T1），将映射方向设置为之前的中心法线方向，点击“auto mapping”即可得到如图12所示网格，记为M′。同样方法可得另一个面N′。

4）使用3D工具栏下的“linear solid”功能可得到如图13所示的规则六面体网格模型中间段，导入有限元通用软件ABAQUS后可建立完整的锈蚀试样计算模型，如图14所示。其中，模型中间段规则六面体网络单元边长约为0.25 mm，沿试样轴向均匀划分为120个单元，中间段总单元数量在14万左右，单元类型为C3D8R。

材料本构关系采用Lemaitre-Chaboche混合强化模型，相关参数如表1所示[21]。表中，σ|0为等效塑性应变为0时的应力;Q∞为屈服面的最大变化值;b为屈服面随塑性应变发展变化的比率;Ci为随动强化模量的初始值;γi为塑性变形增加时随动强化模量减小的比率。

加载采用一端约束，另一端施加强制位移循环荷载的方式进行。根据此前课题组试验结果[11]，Q345钢完好试样在应变幅为2.5%时，断口形貌即表现为延性断裂。为了确保计算结果属于能够反映钢材在强震下反应特征的超低周疲劳破坏，试验段轴向应变幅设置为6%，应变比R=-1，试验段应变幅使用UAMP子程序控制，加载方式如图15所示。

3.3 锈蚀试样的超低周疲劳开裂预测结果

为了直观地观察试验在循环荷载下的开裂位置，采用UVARM子程序将断裂判据CVGM嵌入有限元计算。计算过程中每一增量步都记录单元等效塑性应变与应力三轴度，代入式（5）进行断裂判断，对发生开裂位置的单元进行标记。每组试样建立2个模型，以及1个完好试样模型，共计9个有限元模型。计算结果如表2所示。

由表2可知，未锈蚀试样的开裂寿命为4个循环，开裂位置为截面中心，而锈蚀试样的开裂寿命均有不同程度的降低。相关试验结果表明，完好试样的开裂位置位于截面中心[21-22]，而蚀坑试样的开裂位置位于蚀坑附近[11]。因此，计算得到的开裂位置与试验相符。

这里根据计算结果，分析表2中锈蚀试样的超低周疲劳开裂寿命。由图16所示，试样A05（质损率约7%）与D04（质损率约10%）锈蚀较为均匀，表面形貌起伏较小，没有明显蚀坑，开裂寿命与未锈蚀试样接近，且较其他带有明显蚀坑的试样开裂寿命更长，开裂位置与未锈蚀试样相似，位于截面内部。这说明均匀锈蚀对试样超低周疲劳寿命的影响十分有限。

对于不均匀锈蚀特征明显的试样，超低周疲劳开裂往往发生在各种不利因素叠加的蚀坑位置。这些不利因素主要有：

1）蚀坑位于截面局部缩小处

试样B01、B11、C12与D08的表面形貌与开裂位置如图17所示。由图可知，锈蚀试样的开裂位置均位于局部最小截面位置。其中，B01与C12表面有溃疡状蚀坑群，B11表面存在明显蚀坑集群，D08表面则有一个半径大、深度浅的单蚀坑，均引起了可观的截面局部缩减，导致等效塑性应变在这些位置快速积累，进而引发超低周疲劳开裂寿命的下降。

2）蚀坑位置靠近试样棱线

如图18所示，试样A02轴向截面积差异不显著，开裂蚀坑位于靠近试样棱线的位置。

从CVGM断裂判据公式中可以看出，材料发生疲劳断裂主要与应力三轴度与等效塑性应变两个因素有关。分析试样A02在第一个荷载循环拉伸至最大时表面应力三轴度与等效塑性应变的分布情况。由图19可知，靠近棱线蚀坑位置的应力三轴度与等效塑性应变水平显著高于其他蚀坑，根据CVGM判据可知开裂位于蚀坑位置。

3）蚀坑深径比较大

如图20所示，试样C02在轴向截面积较为均匀，表面存在明显蚀坑a、b与c，深径比分别为0.19、0.29、0.19，开裂位置位于深径比较大的蚀坑b处。如图21所示，该处应力三轴度水平相对较高，等效塑性应变累积速度也更快，因此更容易发生开裂。

总之，锈蚀表面形貌复杂，锈蚀试样的超低周疲劳开裂寿命受多种不利因素耦合影响，包括蚀坑所处截面积、蚀坑位置与蚀坑形状特征等，单一变量无法准确描述可能导致试样疲劳开裂发生的位置。因此，在目前锈蚀结构超低周疲劳性能研究中，从结构易损位置的实际形貌入手进行分析较为妥当。值得一提的是，锈蚀60 d以上各组试样的分形维数与粗糙度区分度较低，超低周疲劳开裂寿命下降程度在各组之中的分布区分度也不明显，因此，也不能推断分形维数、粗糙度与超低周疲劳开裂寿命之间没有相关性。

4 结论

以Q345钢材为对象，对人工加速锈蚀试样进行了表面形貌的扫描测量，依照扫描结果，建立了适合超低周疲劳计算分析的锈蚀试样六面体单元有限元模型，在计算精度上较现有的四面体单元模型更加精确。基于CVGM模型对锈蚀钢材试样超低周疲劳开裂机理与性能进行分析，得到以下结论：

1）人工加速锈蚀试验中，锈蚀速率在开始阶段最快，锈层完全覆盖之后锈蚀几乎停滞，待锈层脱落锈蚀速率略有回升。

2）不同锈蚀时长的各组试样表面二维轮廓扫描处理后得到的粗糙度、分形维数与功率谱密度函数结果区分度不大，是否适合准确评价试样表面的锈蚀程度有待验证。

3）由基于CVGM断裂判据的锈蚀试样数值分析结果可知，锈蚀会降低钢材的超低周疲劳寿命。开裂寿命受均匀锈蚀的影响较小，且疲劳开裂发生于截面内，类似完好试件;受不均匀锈蚀的影响较大，锈蚀试样的开裂多发生于各种不利因素叠加的蚀坑位置。

4）不均匀锈蚀引起的不利因素主要为局部截面积减小、蚀坑位置靠近试样棱线以及蚀坑深径比较大。疲劳开裂寿命受这些不利因素耦合影响，单一变量无法准确描述可能发生开裂的位置。

参考文献：

[1] MILLER D K. Lessons learned from the Northridge earthquake [J]. Engineering Structures， 1998， 20（4/5/6）： 249-260.

[2] NAKASHIMA M， INOUE K， TADA M. Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake [J]. Engineering Structures， 1998， 20（4/5/6）： 271-281.

[3] 黄学伟， 张旭， 苗同臣. 建筑结构钢超低周疲劳断裂破坏的损伤预测模型[J]. 工程力学， 2017， 34（6）： 101-108.

HUANG X W， ZHANG X， MIAO T C. A damage prediction model forultra low cycle fatigue failure of building structural steel [J]. Engineering Mechanics， 2017， 34（6）： 101-108.（in Chinese）

[4] RAHGOZAR R. Remaining capacity assessment of corrosion damaged beams using minimum curves [J]. Journal of Constructional Steel Research， 2009， 65（2）： 299-307.

[5] 名取暢， 西川和廣， 村越潤， 等. 鋼橋の腐食事例調査とその分析[J]. 土木學会論文集， 2001（668）： 299-311.

NATORI T， NISHIKAWA K， MURAKOSHI J， et al. Study on characteristics of damages in steel bridge members[J]. Proceedings of Japan Society of Civil Engineering， 2001（668）： 299-311. （in Japanese）

[6] 柯伟. 中国工业与自然环境腐蚀调查[J]. 全面腐蚀控制， 2003， 17（1）： 1-10.

KE W. Current investigation into the corrosion cost in China [J]. Total Corrosion Control， 2003， 17（1）： 1-10.（in Chinese）

[7] APOSTOLOPOULOS C A. Mechanical behavior of corroded reinforcing steel bars S500 stempcore under low cycle fatigue [J]. Construction and Building Materials， 2007， 21（7）： 1447-1456.

[8] HAWILEH R A， ABDALLA J A， TAMIMI A A， et al. Behavior of corroded steel reinforcing bars under monotonic and cyclic loadings [J]. Mechanics of Advanced Materials and Structures， 2011， 18（3）： 218-224.

[9] 李晓章， 谢旭， 潘骁宇， 等. 拱桥吊杆锈蚀高强钢丝疲劳性能试验研究[J]. 土木工程学报， 2015， 48（11）： 68-76.

LI X Z， XIE X， PAN X Y， et al. Experimental study on fatigue performance of corroded high tensile steel wires of arch bridge hangers [J]. China Civil Engineering Journal， 2015， 48（11）： 68-76.（in Chinese）

[10] 郑祥隆， 谢旭， 李晓章， 等. 锈蚀钢丝疲劳断口分析与寿命预测[J]. 中国公路学报， 2017， 30（4）： 79-86.

ZHENG X L， XIE X， LI X Z， et al. Fatigue fracture surface analysis and fatigue life estimation of corroded steel wires [J]. China Journal of Highway and Transport， 2017， 30（4）： 79-86.（in Chinese）

[11] 宋方远， 谢旭. 锈蚀对钢材低周疲劳性能的影响分析[J]. 浙江大学学报（工学版）， 2018， 52（12）： 2285-2294.

SONG F Y， XIE X. Effect analysis of corrosion on low cycle fatigue behavior of structural steel [J]. Journal of Zhejiang University （Engineering Science）， 2018， 52（12）： 2285-2294.（in Chinese）

[12] 孔德英， 王守琰， 宋诗哲. 金属材料腐蚀形貌图像与实海挂片数据的相关性研究[J]. 中国腐蚀与防护学报， 2001， 21（6）： 352-356.

KONG D Y， WANG S Y， SONG S Z. Study on relativity between corrosion images and data of metallic samples in seawater [J]. Journal of Chinese Society for Corrosion and Protection， 2001， 21（6）： 352-356.（in Chinese）

[13] 徐善华， 何羽玲， 秦广冲， 等. 钢材锈蚀率与表面三维粗糙度参数的关系[J]. 材料科学与工程学报， 2016， 34（2）： 292-295.

XU S H， HE Y L， QIN G C， et al. Relationship between steel corrosion ratio and 3D surface roughness parameters [J]. Journal of Materials Science and Engineering， 2016， 34（2）： 292-295.（in Chinese）

[14] 王皓， 徐善華， 苏磊. 加速腐蚀环境下钢板表面坑蚀形貌统计规律[J]. 土木建筑与环境工程， 2016， 38（1）： 23-29.

WANG H， XU S H， SU L. Statistical regularity of surface pitting morphology of steel in accelerated corrosion environment [J]. Journal of Civil， Architectural & Environment Engineering， 2016， 38（1）： 23-29.（in Chinese）

[15] 徐善华， 张宗星， 秦广冲. 考虑腐蚀钢板表面形貌的三维逆向重建及力学性能退化分析[J]. 材料科学与工程学报， 2017， 35（1）： 81-86.

XU S H， ZHANG Z X， QIN G C. Three-dimensional reconstruction and degradation of mechanical properties based on real surface of corrosion steel [J]. Journal of Materials Science and Engineering， 2017， 35（1）： 81-86.（in Chinese）

[16] KUWAMURA H. Transition between fatigue and ductile fracture in steel [J]. Journal of Structural Engineering， 1997， 123（7）： 864-870.

[17] 赵婷婷， 徐善华， 孔正义， 等. 碳钢人工加速腐蚀试验研究[J]. 水利与建筑工程学报， 2010， 8（2）： 13-15.

ZHAO T T， XU S H， KONG Z Y， et al. Study on accelerated corrosion tests of carbon steel [J]. Journal of Water Resources and Architectural Engineering， 2010， 8（2）： 13-15.（in Chinese）

[18] MANDELBROT B B， PASSOJA D E， PAULLAY A J. Fractal character of fracture surfaces of metals [J]. Nature， 1984， 308（5961）： 721-722.

[19] 曾文曲. 分形理论与分形的计算机模拟[M]. 沈阳： 东北大学出版社， 1993.

ZENG W Q. Fractal theory and its computer simulation[M]. Shenyang： Northeast University Press， 1993.

[20] KANVINDE A， DEIERLEIN G G. Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue [J]. Journal of Engineering Mechanics， 2007， 133（6）： 701-712.

[21] LI S L， XIE X， LIAO Y H. Improvement of cyclic void growth model for ultra-low cycle fatigue prediction of steel bridge piers [J]. Materials， 2019， 12（10）： 1615.

[22] LIAO F F， WANG W， CHEN Y Y. Parameter calibrations and application of micromechanical fracture models of structural steels [J]. Structural Engineering and Mechanics， 2012， 42（2）： 153-174.

（編辑 胡玲）