返璞归真寻童趣 删繁就简守初心
2021-09-10曾红光
曾红光


摘要:2021年5月28日至6月22日我有幸加入了荆州市初中数学中考命题组,6月24日至6月28日又参与了中考评卷工作,从命题组的命题到学生的答题情况,作为一线教师的我,深感学生的学习习惯和思维品质的重要,让我再次静下来思考“回归”,如何喚醒学生的学习欲望,激发学生的学习兴趣。我要做好两件事:一是关注生活,收集情境,以“境”入“理”,学习真实数学,重建课堂新环境;二是开展命题、说题活动,以“评”促“教”,倒逼教学改革,重塑课堂新样态。
关键词:命题 评卷 回归 兴趣
中考命题对教学的发展与评价具有重要的意义,不仅是对教师基本功与专业素养的考察,对教师的教学有着非常重要的指导意义;也对学生掌握必备的基本知识、基本技能,培养学生的抽象思维和推理能力,培养学生的创新意识和实践能力,促进学生在情感态度与价值观等方面的发展,为学生的未来生活、工作和学习奠定重要基础。著名数学家波利亚在《如何解题》中曾说过:如何解题,回到概念。“回归”才是高效,“从简”才能高效。根据《义务教育数学课程标准(2011年版)》中指出:数学教学活动,特别是课堂教学应激发学生兴趣,调动学生的积极性,鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。如何塑造新形势下的新课堂,我将从提高学生的学习兴趣谈谈几点思考:
一.人性的回归
教学活动是师生积极参与,交往活动、共同发展的过程。学生要喜欢数学,首先要从对不讨厌数学老师开始,要对数学教师有敬爱之心。爱上一个人,恋上一座城。教师可以给学生分享自己的专业成长之路,还可以分享自己在坚持个人爱好或特长中的感受。如马拉松运动过程中的体验,马拉松人身体和灵魂总有一个在路上的坚持不懈的精神传递给学生。学习就是一场马拉松,人生就是一场马拉松。世上没有凭白无故的爱,爱,是相互的,也是有传递性的。教师要多走近学生的生活,走进学生的心灵,让学生从心里去“敬”和“爱”老师,才能让学生产生对数学学科求知的欲望与兴趣。
二.课堂的回归
课堂是学生学习和成长的主阵地,教师要紧紧抓住课堂这个中心,结合学生的特点,结合学生的认知规律和心里特征激发兴趣。
1.认真阅读的习惯,培养良好的审题品质,培养数学启蒙的学习兴趣。读题必须认真、仔细,通过读题来理解题意,实践证明,学生不会做,往往源于不理解题意。一旦了解题意,其数量关系也将明了。因此,从这个角度上讲,理解了题意就等于成功的一半。我们有的学生拿到题目后急于得结论,心浮气躁,往往容易出现的错误有:(1)没有读懂题意。(2)审题时漏看、错看已知条件和问题。(3)漏看题目中的条件。(4)找不到题中隐含条件,等等。这些我们觉得都是使学生“解题无从下手”、“解答易错易混”的原因。
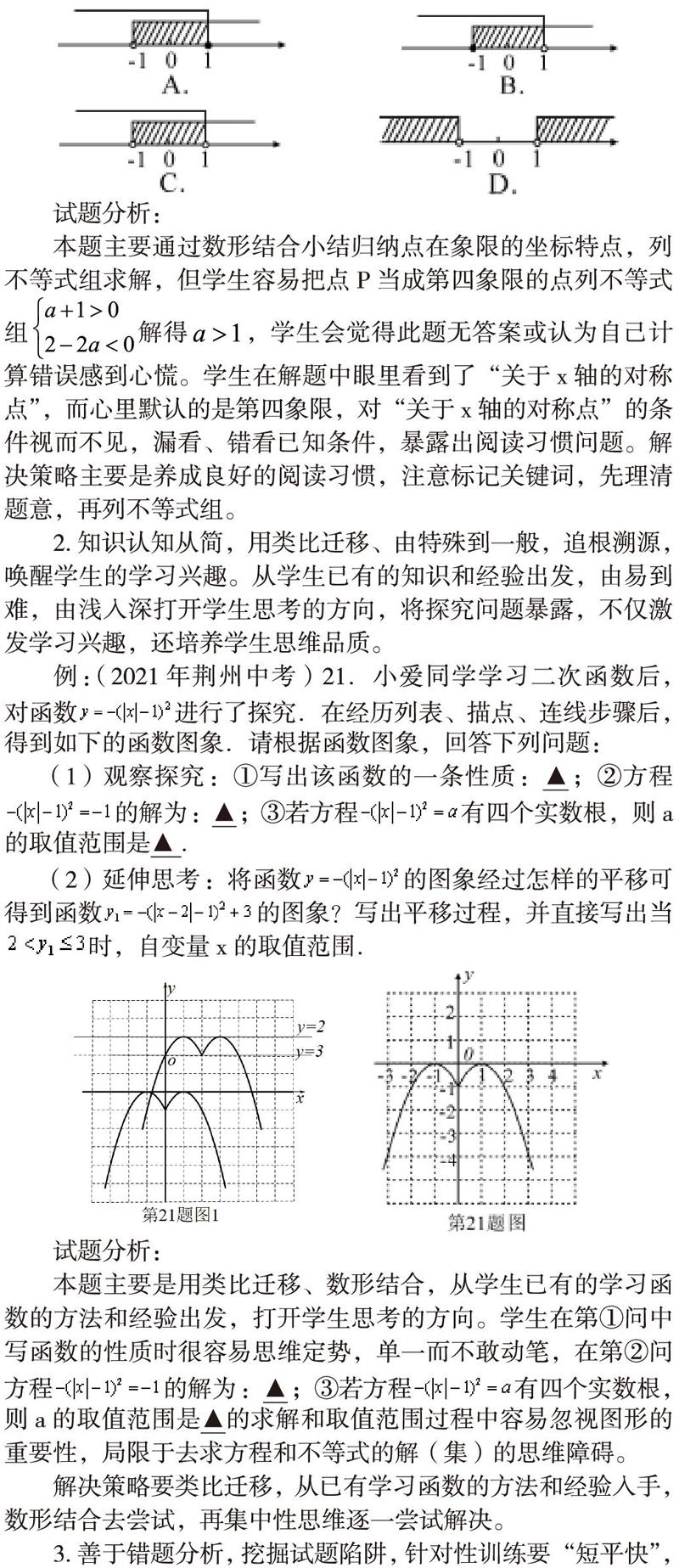
例:(2021年荆州中考)5.若点P(a+1,2-2a)关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为
试题分析:
本题主要通过数形结合小结归纳点在象限的坐标特点,列不等式组求解,但学生容易把点P当成第四象限的点列不等式组解得,学生会觉得此题无答案或认为自己计算错误感到心慌。学生在解题中眼里看到了“关于x轴的对称点”,而心里默认的是第四象限,对“关于x轴的对称点”的条件视而不见,漏看、错看已知条件,暴露出阅读习惯问题。解决策略主要是养成良好的阅读习惯,注意标记关键词,先理清题意,再列不等式组。
2.知识认知从简,用类比迁移、由特殊到一般,追根溯源,唤醒学生的学习兴趣。从学生已有的知识和经验出发,由易到难,由浅入深打开学生思考的方向,将探究问题暴露,不仅激发学习兴趣,还培养学生思维品质。
例:(2021年荆州中考)21.小爱同学学习二次函数后,对函数进行了探究.在经历列表、描点、连线步骤后,得到如下的函数图象.请根据函数图象,回答下列问题:
(1)观察探究:①写出该函数的一条性质:▲;②方程的解为:▲;③若方程有四个实数根,则a的取值范围是▲.
(2)延伸思考:将函数的图象经过怎样的平移可得到函数的图象?写出平移过程,并直接写出当时,自变量x的取值范围.
试题分析:
本题主要是用类比迁移、数形结合,从学生已有的学习函数的方法和经验出发,打开学生思考的方向。学生在第①问中写函数的性质时很容易思维定势,单一而不敢动笔,在第②问方程的解为:▲;③若方程有四个实数根,则a的取值范围是▲的求解和取值范围过程中容易忽视图形的重要性,局限于去求方程和不等式的解(集)的思维障碍。
解决策略要类比迁移,从已有学习函数的方法和经验入手,数形结合去尝试,再集中性思维逐一尝试解决。
3.善于错题分析,挖掘试题陷阱,针对性训练要“短平快”,提高效率,在收获中体验学习兴趣。学生往往急于完成任务或忙于刷题,总时“来也匆匆、去也匆匆”,很少停下来小结、反思。学生若习惯将成功或失败归因于自身因素,会增强后阶段自身行为的努力,培养良好的学习品质和人格品质。
例:(2021年荆州中考)10.定义新运算“※”:对于实数m,n,p,q,有[m,p]※[q,n]mn+pq,其中等式右边是通常的加法和乘法运算,例如:[2,3]※[4,5]25+3422.若关于x的方程[,x]※[5-2k,k]0有两个实数根,则k的取值范围是
A. B. C. D.
试题分析:本题是新定义试题,入口宽,出口窄,学生的思维和解题方法没有障碍,但易错易混。学生对所得方程有两个实数根,容易进入题目设计的陷阱得,而忽略,出错之后往往还认为自己没注意,不引起足够的重视。解决策略注重错题的小结和反思,类比题组,远离陷阱。
4.巧妙的设计“一题多解”“一题多变”,赋予学生足够的思维空间,助于学生丰富的生成,培养学生的探究兴趣。问题是学习的“心脏”,本题怎么做?为什么要这样做?自己是怎样做的?还可以怎样做?学习活动用问题激发,“立足于数学学科本质,使学生有疑问产生”,培养学生良好的思维品质和创新意识。
例:(2021年荆州中考)24.已知:直线与x轴、y轴分别交于A,B两点,点C为直线AB上一动点,连接OC,∠AOC为锐角,在OC上方以OC为边作正方形OCDE,连接BE,设BEt.
(1)如图1,当点C在线段AB上时,判断BE与AB的位置关系,并说明理由;
(2)直接写出点E的坐标(用含t的式子表示);
(3)若tan∠AOCk,经过点A的抛物线顶点为P,且有
6a+3b+2c0,△POA的面积为.当时,求抛物线的解析式.
试题分析:本题以直角坐标系为依托对数学知识的综合考查,既有很强的综合性,又有可操作性,通过学生自主探索,认识和掌握的一次函数、正方形图形的性质,帮助学生积累活动经验,培养学生的发散思维、空间观念、几何直观、运算能力、推理能力、应用意识等。
荆州市本次中考参考人数为46980人,此题得0分有1万多人,得1分(判断)的有2万多人,满分241人,暴露出学生做题没有先易后难的做题习惯,也反应了学生对做最后一题的时间和题目位置方面的心理压力。学生解题方法的思维暴露过程:(1)学生利用由直线yx+1得:由A (1,0),B(0,1)得OAOB,△OAB为等腰直角三角形,∠OAC∠ABO45° ,由正方形OCDE得:OCOE,∠EOB∠AOC 可证△AOC≌△BOE(SAS)得达到目的,但证∠EOB∠AOC时学生很多找不到切入点;(2)有的学生也先证△AOC≌△BOE(SAS)后,利用三角形绕O点旋转90°判断;(3)有的学生先过C、E向轴作了垂线,证,设了点C坐标得到点E的坐标,分别表示出BE、BC、CE的长利用勾股逆定理得出;(4)有的学生先由正方形OCDE四点共圆,再由判断点E在圆上,由直径对直角的;(5)有的学生先过C、E向轴作了垂线,证,设了点C坐标得到点E的坐标,求出直线BE的解析式:,由得。其中法(1)(2)(3)都属于常规思维,法(4)的知识点是课标中没有强调理解、掌握的内容,法(5)的知识点属高中的内容。在第(2)问写出E点的坐标中,大多数学生只写了点C在线段AB上的情况,没有分类考虑在线段AB的延长线上的情况。第(3)问学生易得含有三个参数的两个方程,而后面又出现了两个参数,很难得到P点的坐标。
学生思维障碍第(1)问在于证∠EOB∠AOC得全等;第(2)问在于考虑点C在线段AB的延长线上的情况;第(3)问在于参数过多。
解决策略:平时的学习中要注重“一題多解”“一题多变”,解题时发散思维,从已有的知识和经验出发,用数学思想和方法去联系与转化,再集中思维逐一尝试。
教学思想方法的凝练过程:分析法和综合法先证∠EOB∠AOC;化归,将线的问题转化成点的问题研究;交轨法,将几何图形关系代数化,代数运算结果几何化;方程方法;分类方法等培养和提升学生的思维品质。
5.动手实践,联系生活实例,能很快的激发学生对学数学知识的求知欲,激发出渴望学习的内驱力。数学与生活之间有千丝万缕的关系,不仅教材中涉及大量的生活元素,数学知识在现实生活中有广泛的应用,数学的最终目的也是为解决生活问题。
例:(2021年荆州中考)14.如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知BC8cm,AB16cm.当AB,BC转动到∠BAE60°,∠ABC50°时,点C到AE的距离为▲cm.(结果保留小数点后一位,参考数据:sin70°≈0.94,≈1.73)
试题分析:题立意与背景是选材学生生活中常见的手机支架,将解直角三角形和相似三角形知识结合,抽象建模,利用方程思想和方法,学生经历直观感知,操作确认,推理计算,有一定的难度。
解题方法的思维暴露,如何列方程求垂线段CD的长。
学生思维障碍首先主要体现在他们已有的列方程的方法常见的有勾股定理、三角函数、相似三角形、面积法等,有直角却无三角形、无特殊角,有此处又无直角、无三角形。学生已有的求解经验一般有三种:①用:直接由已知条件列方程;②换:将要求解的量进行代换后求得;③构:构造特殊图形列方程求解。
解决策略:就要先在特殊角构造直角,延长BC构造三角形,化归到已有的知识来解决。
第二个思维障碍在于如何求CD?解决策略:发散思维,顺其自然,从题目已有的条件出发,先用三角函数知识求BG,再求BF,分步进行,再集中性思维利用相似三角形的性质列方程求CD,
6.应用合作学习,提高学生学习兴趣和积极性,增强学生的自信心。利用小组合作学习下学生讲题,将学生分成若干个小组,可以让学生发挥主体作用,使其在小组内围绕共同的问题思考、分析、探索,提出各自的见解与看法,体验成功的喜悦,增强学生的学习兴趣和信心,形成良好的学习氛围,促使深度思维,深度学习的发生,在辩论中让辩论性思维获得成长。
7.合理引用信息技术,激发学习动机与学习期待,提升专注力与行动力,发展空间想象和思维创造力。多媒体能将抽象的数学知识具体直观的呈现出来,还可以培养学生的想象能力,进一步体会到几何图形的“变”与“不变”,从而完成从试验几何到推理几何的思维训练和提升,激发兴趣,形成深度认知。
三.生活的回归
1.数学现实的回归
陶行知先生说:“教育应以生活为中心,没有生活做中心的教育是死教育,没有生活做中心的书本是死书本。”《义务教育数学课程标准(2011年版)》中指出:贴近学生生活实际来甄选有利于学生的体验与理解、思考与探索的数学课堂内容,让学生感受数学与现实的联系,用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界,用数学的理性精神反思现实问题,增强学生对数学的学习兴趣。
例:(2021年荆州中考)20.高尔基说:“书,是人类进步的阶梯.”阅读可以启智增慧,拓展视野,……为了解学生寒假阅读情况,开学初学校进行了问卷调查,并对部分学生假期(24天)的阅读总时间作了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为(小时),阅读总时间分为四个类别:A,B,C,D,将分类结果制成如下两幅统计图(尚不完整).
根据以上信息,回答下列问题:
(1)本次抽样的样本容量为▲;
(2)补全条形统计图;
(3)扇形统计图中的值为▲,圆心角β的度数为▲;
(4)若该校有2000名学生,估计寒假阅读的总时间少于24小时的学生有多少名?对这些学生用一句话提一条阅读方面的建议.
试题分析:本题以“阅读”为载体,将数据的收集、整理、分析巧妙的结合,立意深刻,内涵丰富,通过条形统计图和扇形统计图描述数据,然后分析得出结论:要重视阅读,养成阅读习惯;要增加阅读时间,提高阅读质量;要培养阅读兴趣,保证阅读时间;要坚持阅读,从今天做起等。
培养学生多角度分析问题、解决问题的能力,引导学生自觉关心身边之事、社会之事和国家之事,普及相关知识,让学生充分体会生活中处处有数学,数学广泛应用于生活。
2.数学人文的回归
数学文化是人类文化的重要组成部分,它具有比数学知识更丰富、深邃的内涵。齐民友先生指出:一个没有相当发达数学文化的民族是注定要衰落的,一个不掌握数学作为一种文化的民族注定是要衰落的。《义务教育数学课程标准(2011年版)》中指出:数学文化作为教材的组成部分,应渗透在整透教材。因此,数学文化理应走进数学活动,融入中考数学命题,让数学升华学生的学习兴趣。
例:(2021年荆州中考)22.小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.
(1)求买一支康乃馨和一支百合各需多少元?
(2)小美准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为w元,康乃馨有x支,求w与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.
试题分析:本题以“母亲节”买花祝福妈妈为载体,将实际问题抽象成数学问题,建立数学模型,应用方程组、不等式、函数思想去设计方案,解决问题,属代数综合性试题。
学生解题方法的思维暴露主要是不遵循知识的形成规律,不能由浅入深,分步进行。不遵循解应用题的一般步骤:审、设、(表示)、列、解、求、验、答。特别是设了未知数或变量后,急于列关系式,忽略用单项式、多项式先去表示其它未知量。违背了我们对知识是经历从数、字母表示数、单项式、多项式、然后等式的认知过程。此题还有“验”这一关,∴的整数随的增大而减小∴当9时,-9+5546(元)。
本题立意深刻,背景内涵丰富,“小美”寓意心灵美,“康乃馨”代表健康和美好,“百合”代表百年好合,“11”代表一心一意,渗透感恩教育。引领教学关注数学文化渗透,关注中华民族传统美德,激励当代学生要有责任感、使命感,真正感受到文化的感染,產生文化共鸣,体会数学的文化品位,实现社会文化和数学文化的互动。
兴趣是最好的老师,是最大的内动力。中考命题对我教学最大的启示并不是大量的“刷题”,不能使用“题海战术”,而是我们要从学生的学习习惯和思维品质抓起,回归到学生的学习兴趣入手去落实数学的学科核心素养。只有充分体现“人”的重要性,“以人为本”,教学理念才能真正落实到课堂的每一个环节,从而提高学生解决问题的能力和数学学科核心素养。
参考文献:
(1)义务教育数学课程标准(2011年版)
(2)党宗权,初中数学教学中提高学生解题水平的途径——中学数学2020(10)
(3)刘成龙、钟梦圆、宋西泠,中考数学命题题材的几种视角——中学数学2020(11)
