数学思维方法视角下物理压轴题的评析
2021-09-10孔祥宇张一驰张洋
孔祥宇 张一驰 张洋


摘 要:高考作为选拔性考试,其物理压轴题分值大、难度高,而且涉及的物理规律多、物理情境新颖、运算过程复杂,考查学生的综合能力。2021年八省联考的试题是一次全员模拟的高考演练,文章对部分压轴题进行详细分析,讨论其中用到的数学思维方法。
关键词:八省联考;物理压轴题;数学思维
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2021)8-0043-4
从物理学的发展史来看,牛顿在建立经典力学过程中创造了微积分,麦克斯韦建立的电磁场理论和数学中矢量分析与经典场论有密切关系,爱因斯坦的广义相对论的基础是黎曼几何。可以说物理的发展和突破离不开数学。因此,高中阶段学好物理不仅要掌握数学工具,更重要的是善于利用数学的思维方法去学物理,两者是不可分的[1]。
2021年初,第三批高考综合改革的河北、辽宁、江苏、福建、湖北、湖南、广东、重庆八省市为全力做好新高考落地的各项工作,进行了全流程全员模拟高考演练。教育部考试中心和各省教育考试院精心制定命题并进行适应性测试,网称“八省联考”。在此背景下,深入研究“八省联考”的试题,对于深入理解高考内容的改革方向具有重要意义。本文将以“八省联考”中物理学科部分压轴题为例,在数学思维方法视角下对物理压轴题进行评析,总结数学思维方法在解决物理压轴题中的作用。
1 分类讨论思想
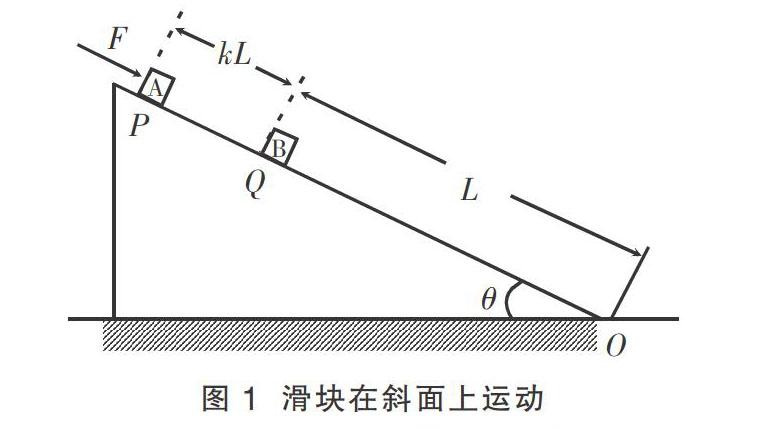
广东卷:如图1所示,固定的粗糙斜面,倾角θ=30°,斜面底端O处固定一个垂直斜面的弹性挡板。在斜面上P、Q两点有材质相同、质量均为m的滑块A和B,A和B恰好能静止,且均可视为质点,Q到O的距离是L,Q到P的距离是kL(k>0)。现始终给A施加一个大小为F=mg、方向沿斜面向下的力,A开始运动,g为重力加速度。设A、B之间以及B与挡板之间的碰撞时间极短,且无机械能损失,滑块与斜面间的最大静摩擦力等于滑动摩擦力。求:
(1)A、B第一次碰撞后瞬间它们的速率分别为多少;
(2)A、B第一次碰撞与第二次碰撞之间的时间。
解析 (1)两物体质量相等,碰撞后速度交换:vA=0,vB=(过程不再赘述)。
(2)第一次碰撞后B做匀速运动,到底端所用的时间为:
A做匀加速运动,aA=g,运动到底端的时间为:
分析tA和tB:若tA
第一种情况:
tA 由gt2=vBt,解得t=2 第二种情况:tA>tB,因此k>,第一次碰撞后,B做匀速运动,B与挡板碰撞时间为 B与挡板碰后原速率返回,由牛顿第二定律可得 mgsinθ+μmgcosθ=maB 解得aB=g A滑块此时的位移为,速度为gt1。此后,A和B的加速度大小、方向相同,A的速度沿斜面向下,B的速度沿斜面向上,因此由相对运动可知 (vB+gt1)(t-t1)= 解得t= 总结:不管是数学还是物理中的结论都有其成立的条件和适用范围,这就导致了有些问题的结论在解题过程中不能以统一的形式进行研究和表述。物理学中的分类讨论往往和临界状态相关联,临界状态前后,物体满足的状态方程发生变化。而本题中的临界状态正是来源于B滑块与弹性挡板的碰撞。在碰撞前后B滑块的速度发生突变,满足不同的运动方程,因而需要分别列式求解。利用分类讨论的思想解决物理问题的一般方法是:首先,分析所有可能的物理情境,进而分析不同物理情境之间的临界点以及对应的关键物理量,将所研究的问题转化成若干子问题,化繁为简,逐步求解。 2 几何作图与求解 重庆卷:有人设计了一种利用电磁场分离不同速率带电粒子的仪器,其工作原理如图2所示。空间中充满竖直向下的匀强电场,一束质量为m、电量为-q(q>0)的粒子以不同的速率从P点沿某竖直平面内的PQ方向发射,沿直线飞行到Q点时进入有界匀强磁场区域,磁感应强度大小为B,方向垂直于该竖直平面,PQ=4l。若速度最大粒子在最终垂直于PT打到M点之前都在磁场内运动,且其他速度粒子在离开磁场后最终都能垂直打在PT上的NM范围内,PM=8l,PN=6l,若重力加速度大小为g,求 (1)电场强度的大小; (2)粒子速度大小的范围; (3)磁场穿过该竖直平面内的最小面积。 解析 第1问比较简单,重力和电场力二力平衡,即可求得电场强度。第2问求粒子速度的大小范围,即求粒子在磁场中运动半径的最大值和最小值。如图3所示,速度最大值对应的圆弧轨迹是O1QM,速度最小值对应的圆弧轨迹是O2QR,而后从磁场射出沿着RN垂直打在PM上。设大圆弧O1QM半径为R1,小圆弧O2QR半径为R2。在直角三角形PQO1中,由几何关系可得 (PO1)2=(PQ)2+R=(PM-R1)2 解得 R1=3l,PO1=5l,∠QPO1=37°,∠QO1P=53° 进一步由几何关系可知,线段PQ、QO2、O2R在PM方向上的投影长度等于PN,可得 PQcos∠QPO1+R2cos∠QO1P+R2=PN 解得R2= 粒子做圆周运动的向心力由洛伦兹力提供,进一步由向心力公式可得粒子的速度范围为 第3问中所求是磁场在竖直平面的最小面积,若粒子速度满足第2问的条件,那么粒子运动范围在圆弧■、圆弧■和線段RM围成的阴影部分。由几何关系可知,阴影部分面积为扇形O1QM的面积减去扇形O2QR和梯形O2O1MR的面积,计算可得 总结:解决电磁学压轴题的核心在于准确描绘出粒子运动的几何图形。粒子在真空中的轨迹是直线,在电场中的轨迹是抛物线,在磁场中的轨迹是圆,磁场或电场的边界可能是直线和曲线的组合。电磁学常见的考查形式集中在由几何关系定圆心求半径、圆心角、时间、位移、速度、磁场区域等问题。因此,在求解此类问题时几何作图能力和由几何关系定量计算的能力尤为重要[2]。 3 二次函数求根 湖南卷:如图4所示,一滑板的上表面由长度为L的水平部分AB和半径为R的四分之一光滑圆弧BC组成,滑板静止于光滑的水平地面上。物体P(可视为质点)置于滑板上面的A点,物体P与滑板水平部分的动摩擦因数为μ(μ<1)。一根长度为L、不可伸长的细线,一端固定于O′点,另一端系一质量为m0的小球Q。小球Q位于最低点时与物体P处于同一高度并恰好接触。现将小球Q拉至与O′同一高度(细线处于水平拉直状态),然后由静止释放,小球Q向下摆动并与物体P发生弹性碰撞(碰撞时间极短)。设物体P的质量为m,滑板的质量为2m。 (1)求小球Q与物体P碰撞前瞬间细线对小球拉力的大小; (2)若物体P在滑板上向左运动从C点飞出,求飞出后相对C点的最大高度; (3)要使物体P在相对滑板反向运动过程中,相对地面有向右运动的速度,求的取值范围。 解析 (1)(2)略。 針对第3问,由动量守恒可得 mv0=mvA+2mvB 由能量守恒可得 联立解得方程 这是一个一元二次方程,首先要求判别式大于零,速度向右说明结果要小于零,则 联立解得 总结:判别式法是数学中解题的常用方法,可用于求值域、求极值、证明不等式以及求解参数的取值范围,本题即是用到了判别式法求解参数的取值范围。此类题目难点在于求解麻烦,求解极值问题或者约束范围问题常会用到。例如2017年全国新课标I卷第25题,涉及到判别式法,计算量大,考生得分率低。因此,平时可以加强此类题目的训练,增强学生对相关方法的熟悉度,针对此类题目要敏锐地发现物理公式在数学上的联系,从物理场景中抽象出数学方程,进而利用熟悉的数学公式实现对问题的快速求解。 4 教学思考与启示 本文所选“八省联考”的三道压轴题中的数学思维方法都很典型,并且综合来看,包含的范围也比较广泛,既有几何问题、函数与方程问题,也有分类讨论的一般思想。这体现了本轮高考内容改革对综合能力考查的重视,也给我们以下启示。 (1)在物理的学习中,数学是重要的一部分,在高中物理学习中,排斥数学是不可取的,如何将数学和物理思维有效结合至关重要。在高中阶段物理教学中不应只强调数学是公式的应用、解方程和计算结果,更重要的是如何把数学的思维方法迁移到物理的学习中[3]。 (2)高中阶段应注重培养学生从具体物理问题中抽象出数学问题的能力,利用物理思维构建整个物理过程,利用物理学规律从具体物理过程中提炼出数学方程式,然后利用分类讨论、几何作图、函数方程、归纳演绎等模块化的数学知识快速求解。 (3)高考物理压轴题的数学计算量普遍较大,例如2020年高考山东卷压轴题涉及到数学中等比数列求和公式,计算量大,求得结果较为耗费时间,对考生的综合能力尤其是计算能力要求较高。因此,在教学中应重视解方程、计算结果,这些不仅仅是数学课上的事情,恰恰也是解决物理压轴题的关键。 参考文献: [1]郭雪鹏.学习物理须重视数学——从2017年高考题谈起[J]. 物理教学探讨, 2018,36(02):40-41. [2]陈宏胜.电磁巧组合 变中求不变——对2013江苏高考物理压轴题的赏析[J].中学物理教学参考,2019,48(11):95-96. [3]徐忠平.提升思维能力 加强数学应用——2020年高考山东物理卷压轴题评析与教学思考[J].物理教师,2020,41(12):79-82. (栏目编辑 陈 洁)
