圆周法平面度误差测量与评定
2021-09-10赵新宇赵则祥刘如意任东旭席建普
赵新宇, 赵则祥, 刘如意, 任东旭, 李 彬, 席建普
(1. 中原工学院计算机学院,河南 郑州 451191; 2. 中原工学院机电学院,河南 郑州 451191)
0 引 言
平面度公差是高精度零件的形状公差项目之一。依据ISO 12781:2011,平面轮廓的测量方案主要有矩形栅格法、极坐标法、三角形栅格法、米字形栅格法、平行线栅格法[1]。上述测量方案中,极坐标法适用于圆平面轮廓的测量,其他则是矩形平面轮廓的测量方案。
Balázs Mikó[2]利用坐标测量机研究了不同测量方案对铣削平面平面度误差测量的影响以及最佳测量点数问题;Nermina Z U等[3]研究了在坐标测量机上采用不同的测头和不同的采样方案对平面度误差测量的影响;Yang Y等[4]研究了基于自适应混合的教育学优化算法在平面度误差评定中的应用,提高了平面度误差最小区域法的评定精度;Zhang Yu 等[5]设计了微型零件的平面度精密测量装置,并进行了平面度误差的最小二乘评定;Zha C Y 等[6]设计了基于激光点的大平面平面度误差的测量系统,利用该系统对大平面平面度误差进行了测量与评定。
对于高精度的圆平面,如回转工作台台面、晶圆平面、回转件的端面以及作为相关要求的圆平面基准等,可在圆(柱)度仪上用极坐标法对圆平面的轮廓进行测量。极坐标法有圆周法、射线法等测量方案,圆周法测量方案测头由圆(柱)度仪横臂移动到所设定的圆周上,工作台在每个设定的圆周上回转一周,在该圆周上测得相应的z向轮廓值;射线法测量方案是将工作台回转至所设定的角度,工作台停止转动,横梁带动测头沿射线径向移动,在该射线上测得相应z向轮廓值。不管是采用圆周法还是射线法的圆平面轮廓提取方案,均可采用最小二乘法[7]和最小区域法[8-9]进行平面度误差评定。最小区域法评定平面度误差,其实质是一个‘minimax’优化问题,可用形状误差(如圆柱度误差、圆度误差、直线度误差等)最小区域评定中常用的优化算法[10-12]和最大最小尺寸的优化算法[13]进行评定。本文基于圆周法的5种采样方案,建立了圆平面的平面度误差的最小二乘法和最小区域法的评定模型,提出了基于平面包容和轮廓包容的两种圆平面的平面度误差评定结果的可视化方法,并通过实验验证了所建评定模型的正确性和可视化方法的可行性。
1 圆平面轮廓的圆周法测量方案
圆周法的测量方案如图1所示,圆周测量方案是极坐标测量方案中的一种方案。
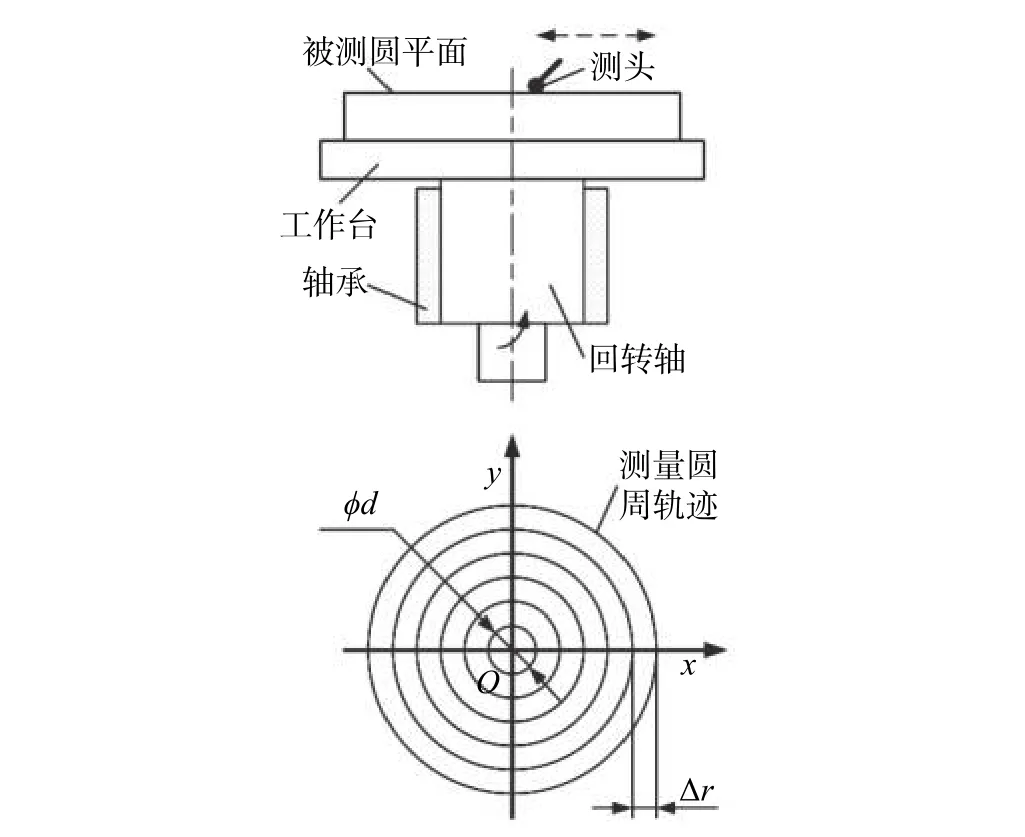
图1 圆周测量方案示意图
圆周测量方案可以是等角度采样,即各圆周上的采样点数相同,也可以是等弧长采样,即各圆周上的采样点数不同,采样点数随圆周的直径增加而增加。圆周间可以是等间隔,也可以随着圆周直径的增大采用不等间隔,尽可能使圆平面上的采样点数相对均匀布置。
根据实际情况,可以是多圆周布置,也可以用一个圆周近似替代。
2 圆平面的平面度误差评定模型
2.1 圆平面轮廓坐标的确定
假设测量圆周数为m,采用等角度和等圆周间隔测量,每个圆周上的采样点数为n,两相邻圆的间隔为Δr,第一个圆周(最小的圆)的直径为d,第i圆周上第j个采样点x和y坐标由下式确定:
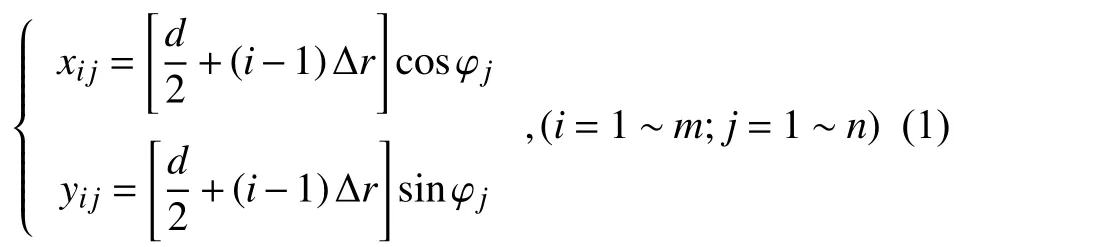
对于等弧长和等周圆间隔测量,由于受仪器结构(如编码器)的限制,实现等弧长测量还是困难的,但可随着测量圆直径的增加,适当增加采样点数较易实现。假定第1个圆周(最小圆周)的采样点数为n1,第i圆周上的采样点数ni可按一定的规律设置,但最大采样点数不能超过测量仪器转台一周的最大采样点数,如Taylor586LT的一周的最大采样点数为18 000,而圆柱体直径与形位误差综合测量仪的一周的最大采样点数为1 000。第i圆周上第j采样点的x和y坐标由下式确定:
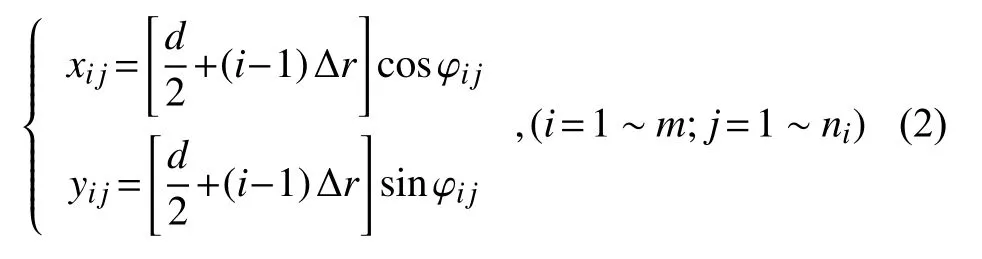

在xij和yij坐标点测得的轮廓值为zij。
当m=1时,用一个圆周上的轮廓值作为该被测圆平面的轮廓。
2.2 圆平面的平面度误差的评定模型
在xoyz坐标系中建立一平面方程,如下式所示:

由式 (3),假设C≠0,有,
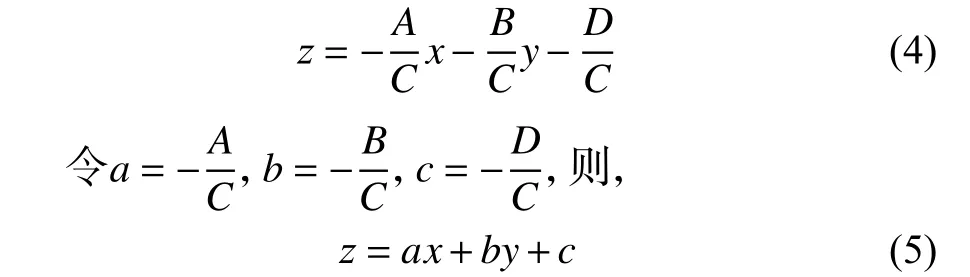
以等角度采样为例,依据所有采样点的坐标(xij,yij,zij),i=1~m,j=1~n,建立平面度误差最小二乘拟合方程为:

由式(6),可得三元一次方程组,即
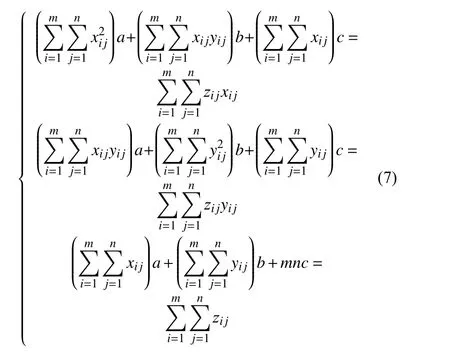
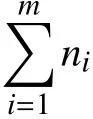
最小二乘平面度参数确定后,可得到第i圆周上第j采样点Pij到该理想平面的垂直距离sij,如图2所示。
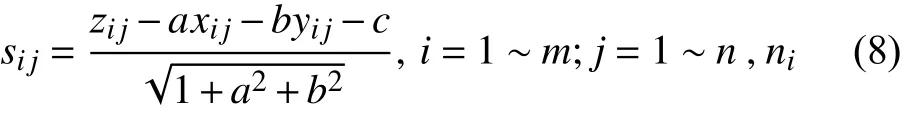
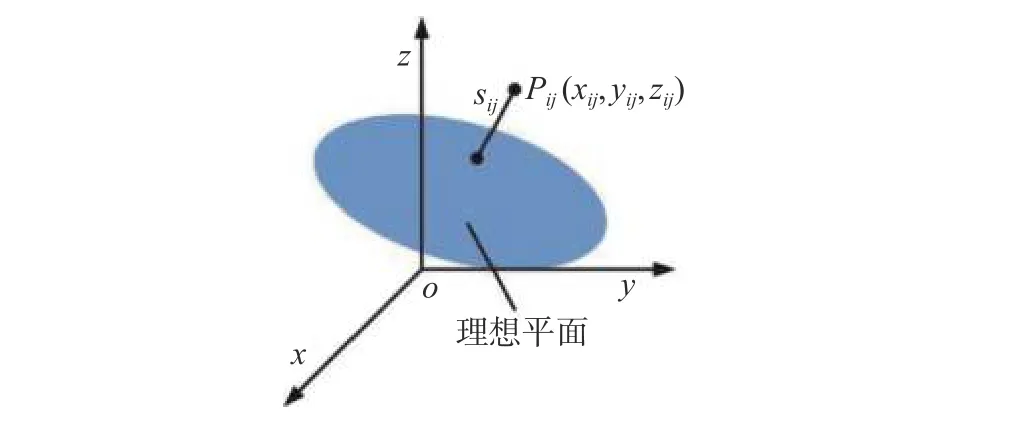
图2 点到理想平面的垂直距离示意图
由最小二乘法得到的平面度误差
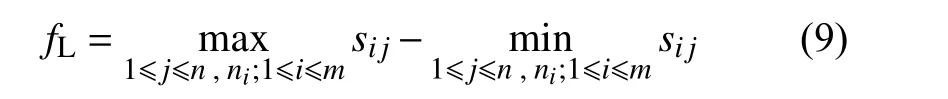
用最小区域法评定圆平面的平面度误差,可表示为:
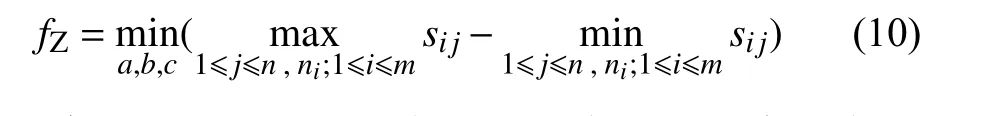
当m=1时,也可以尝试用圆度误差评定的方法进行处理。首先进行数据转换,将测得的z1j作为径向微小变动量,则第j采样点的径向值可表示为
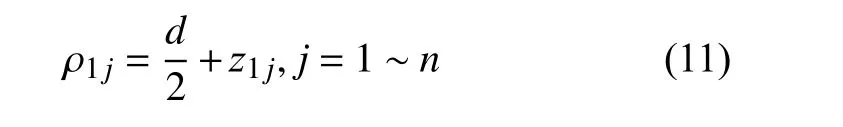
其中d的含义见式(1)或式(2)。
当m=1时,平面度误差的评定结果可近似由图3所示的圆度误差的评定结果替代,即


图3 平面轮廓转化为圆周轮廓的示意图
关于最小二乘法和最小区域法确定圆心坐标x0和y0的算法见文献[7-8]。
3 程序编制
最小区域法圆平面的平面度误差通过对式(10)和式(12)的优化问题采用Matlab中的‘fminimax’函数获得,最小区域平面参数的优化初始值均是最小二乘平面参数值。将Matlab中的plot3三维绘图函数与hold on语句组合使用,把m个圆周上的轮廓、相关理想平面呈现在一张图上。对于圆周轮廓的理想包容面(或最小二乘平面)的显示,可利用各圆周对应的理想圆周表示,也可用Matlab中的surf或mesh函数生成的理想平面显示。对于用一个圆周表示圆平面轮廓的测量,当用图3所示的圆周轮廓表示圆平面轮廓时,为使评定结果的可视化,将测得的轮廓值(z1j,j=1~ni)适当放大,可得到放大后的轮廓,用最小二乘圆表征最小二乘平面,用两个同心圆包容圆周轮廓代替用两个平面包容圆平面轮廓。
4 实 验
在Talyround585LT圆柱度仪对其工作台圆平面进行了轮廓提取,并将轮廓数据以‘.CVS’格式导出。采用等间隔等角度、等间隔不等角度和单圆周等三种轮廓测量方案,测量方案参数如表1所示。表2给出该工作台圆平面的平面度误差评定结果。

表1 轮廓测量方案参数
图4为采用等间隔等角度测量方案(方案1)的平面度误差的可视化评定结果;图5为采用等间隔不等角度测量方案(方案2)的平面度误差的可视化评定结果;图6为单圆周测量方案(方案3)的平面度误差的可视化评定结果;图7为采用单圆周测量方案(方案3)和圆周法的平面度误差的可视化评定结果。图4(a)和图5(b)为圆轮廓对实际轮廓包容;图4(b)和图5(a)为圆平面对实际轮廓包容。由表2和图4~ 图6可以看出,测量方案对平面度误差评定结果具有一定的影响,方案3对测量结果的影响较大,在测量仪器和被测结构允许的情况下,建议不采用方案3对圆平面的平面度误差进行测量。由图6和图7可以看出,两种评定方法的评定结果相同,圆周法可用于圆平面的单圆周测量方案的平面度误差的评定。

表2 平面度误差评定结果

图4 平面度误差评定结果可视化(方案1)
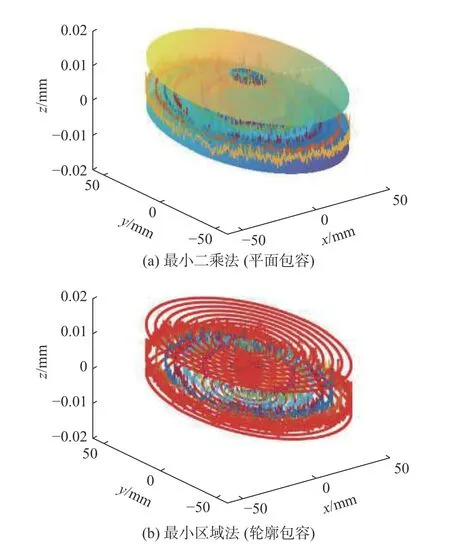
图5 平面度误差评定结果可视化(方案2)
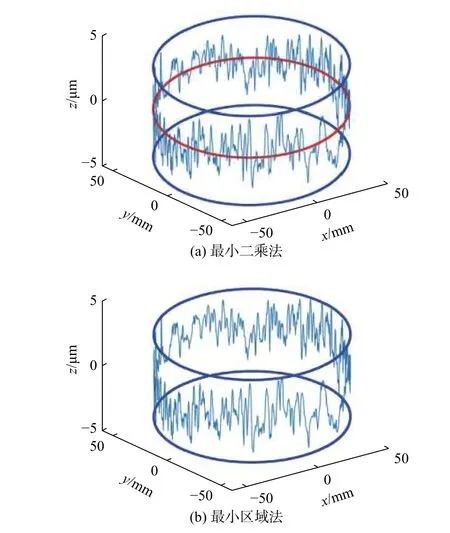
图6 平面度误差评定结果可视化(方案3)
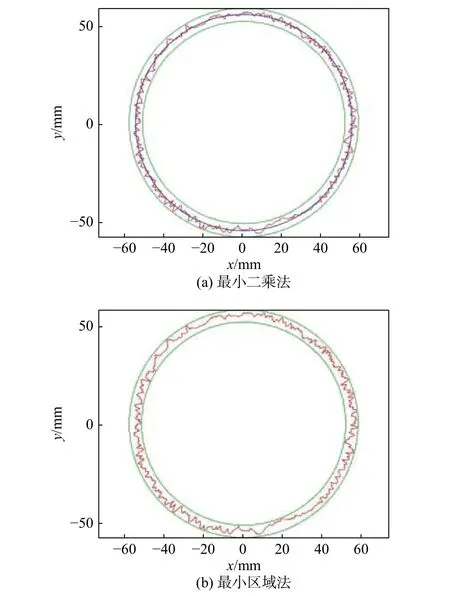
图7 平面度误差评定结果可视化(方案3圆周法)
5 结束语
基于圆周法的三种测量方案,研究了圆平面的平面度误差的测量与评定中的数据处理问题,建立了圆平面的最小二乘法和最小区域法的平面度误差评定模型。对于圆平面的单圆周的轮廓测量方案,提出了基于圆度误差评定模型的圆平面的平面度误差的评定方法。依据上述圆平面轮廓的圆周法测量方案和平面度误差评定模型,编制了圆平面的平面度误差评定及其结果的可视化程序。对一圆平面按三种测量方案进行了轮廓测量,并用所编制的程序进行了平面度误差评定和结果的可视化,程序运行结果验证了所建评定模型的正确性,并验证了单圆周测量方案情形下两种平面度评定方法的一致性。
