高强IF钢应变硬化模型研究及在仿真对标中的应用
2021-09-10王连轩张秀宏牛月鹏
王连轩,张秀宏,牛月鹏
(河钢集团邯钢公司技术中心,河北 邯郸 056015)
材料力学性能多指五大指标,即材料的屈服强度、抗拉强度、断后伸长率和断面收缩率以及一次冲击 a k 值[1]。长期以来,汽车零件一直是以材料的屈服强度、抗拉强度等基本力学性能指标作为设计的依据,并以此来预测零件的静态性能[2]。而随着计算机技术、数字模拟技术的发展,材料的应变硬化模型在结构设计、先进成形工艺仿真和安全仿真分析中得到了广泛应用[3-6]。在进行计算机仿真计算时,比如成形分析、刚度分析、强度分析、碰撞性能分析,需要以材料的真实应力-塑性应变曲线为输入,该曲线是否能够正确反映材料的真实性能是仿真分析关键。通过拉伸试验机可以获得材料的工程应力-应变曲线,但由于缩颈后的曲线并不能代表材料真实的应变强化,需要通过采用本构方程进行拟合外推。目前常用的拟合外推的模型包括Ludwik本构方程、Swift本构方程、Gosh本构方程、Hockett-Sherby本构方程、Swift- Hockett-Sherby混合本构方程等。本文通过验证,采用Swift本构方程拟合外推的曲线应变硬化强度高,采用Hockett-Sherby本构方程拟合外推的曲线应变硬化强度弱。因此本文通过采用加权系数构成Swift- Hockett-Sherby混合应变硬化模型,并采用仿真对标确定合适的加权系数。
1 拉伸试验设备介绍
采用Zwick/Roell Z100XL型全自动电子拉力试验机进行拉伸试样。Zwick/Roell Z100XL型是全自动电子拉力试验机,其最大的优势就是拉伸试验试样的夹持一致性高,避免人为夹持不对称、倾斜等缺点。Zwick/Roell Z100XL型全自动电子拉力试验机配置全自动纵向和横向引伸计、全自动横截面测量台、TestXpert智能测试软件。整台设备可以满足金属试样的全自动拉伸试验测试要求,以及金属薄板n值、r值试验要求。具备检测IF钢、低合金高强钢、双相钢、马氏体钢等汽车板材料的基础拉伸性能和应力应变曲线的测试。
2 拉伸试样尺寸及测试方法
高强IF钢试样采用GB/T 228.1-2010标准中规定的P6试样(见图1),矩形试样,其中L0=80 mm,b0=20 mm。L0为试样原始标距,0为试样平行长度的原始宽度。为了减小应变速率硬化效果,提高试验的准确性。材料发生屈服前应力速率最大60 MPa/s,材料在塑性范围和直至抗拉强度应变速率不超过0.0025/s。
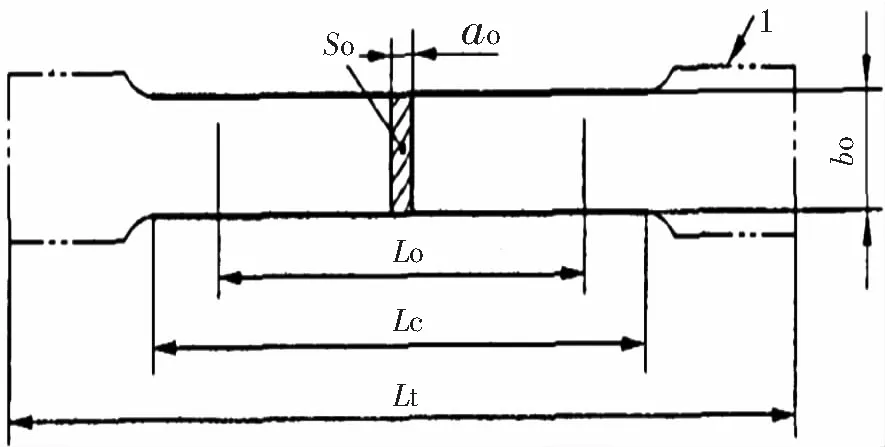
图1 拉伸试样示意图
3 试验材料及力学性能
试验材料为CR180IF和CR260IF,裸板,材料力学性能见表1所示。
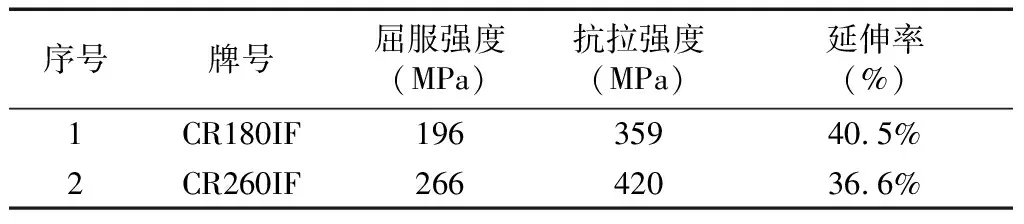
表1 力学性能
4 工程应力-应变曲线的检测与数据处理
通过Zwick/Roell Z100XL型拉力试验机获得CR180IF和CR260IF工程应力-应变曲线(见图2所示),其中工程应力为载荷与试样原始横截面之比,工程应变为原始标距的伸长与原始标距L0之比。CR180IF在抗拉强度(358.7 MPa)后发生缩颈,缩颈点对应的工程应变为0.210。CR260IF在抗拉强度(420.3 MPa)后发生缩颈,缩颈点对应的工程应变为0.208。利用公式1-3将工程应力和工程应变分别转化为真实应力和塑性应变,并去掉缩颈点以后的曲线获得真实应力-塑性应变曲线(见图2所示)。
真实应变计算方法,εT=ln(1+ε),ε为工程应变。(1)
真实应力计算方法,στ=σ*(1+ε),σ、ε分别为工程应力应变(2)
塑性应变计算方法,εplastic=ετ-στ/E
(3)
其中,εplastic为塑性应变,ετ为真实应变,στ为真实应力,E为弹性模量。
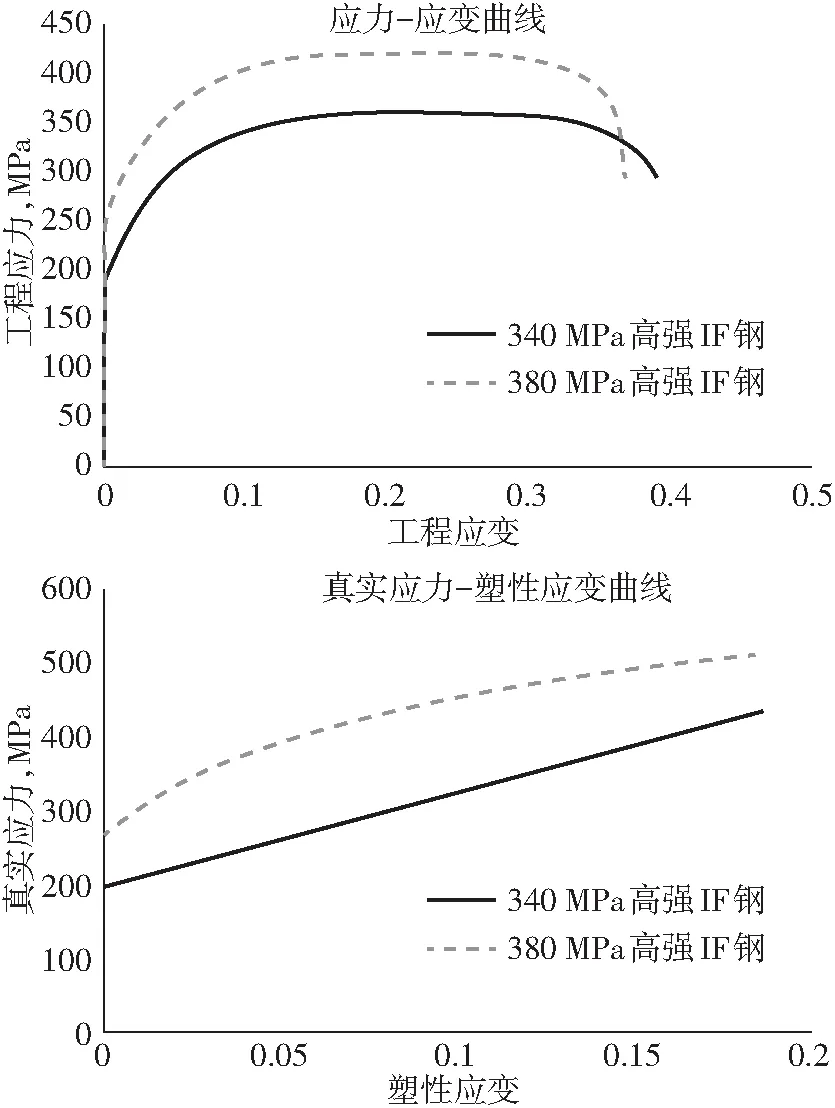
图2 应力-应变曲线
5 本构方程拟合
获得真实应力-塑性应变曲线后,采用Swift- Hockett-Sherby混合本构方程对真实应力-塑性应变曲线进行统一拟合外推到1。其中Swift- Hockett-Sherby混合本构方程如下:
(1)Swift本构方程:
σ=c*(εp1+εD)m
(2)Hockett-Sherby本构方程:
σ=σsat-(σsat-σi)e
(3)Swift- Hockett-Sherby混合本构方程:
σ=(1-α)*[*(εp1+εD)m]+α*[σsat-(σsat-σi)e]
首先拟合Swift本构方程,获得c、εD、m三个系数,然后拟合Hockett-Sherby本构方程,获得σsat、σi、α、p四个参数,拟合参数见表2所示。

表2 拟合参数
以CR260IF为例,不同加权系数本构方程的拟合曲线见图3所示,并与获得的真实应力-塑性应变曲线对比。加权系数α=0的曲线可以认为是Swift本构方程,α=1的曲线可以认为是Hockett-Sherby本构方程。从拟合曲线看,在缩颈前Swift和Hockett-Sherby本构方程都能够很好的拟合真实应力-塑性应变曲线。但是缩颈后,Swift本构方程的应变硬化的强度远大于Hockett-Sherby本构方程。通过不同的加权系数α,可以改变缩颈后材料的应变硬化强度。
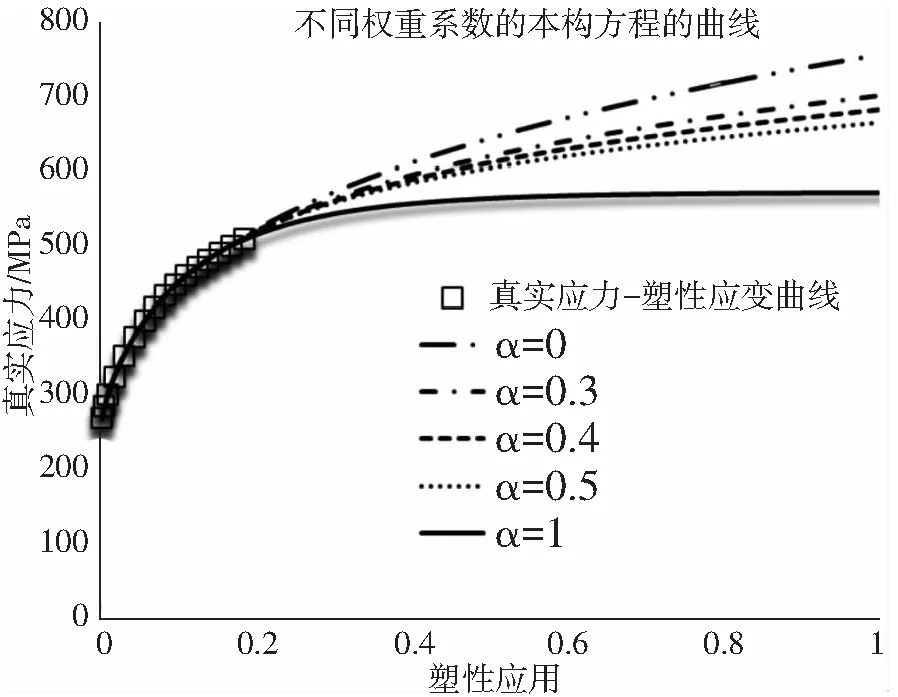
图3 不同权重系数的本构方程拟合曲线
6 仿真对标分析
按照实际拉伸试样尺寸建立拉伸仿真模型,具体见图4所示。为了保证仿真的准确性,采用实体模型,厚度2 mm。试样一端约束,另一端加载1 mm/s速度。输出载荷力和位移曲线,计算工程应力-应变曲线。
采用不同的α参数输入仿真模型进行计算,计算获得工程应力-应变仿真曲线,并与拉伸试验机检测的工程应力应变曲线进行对比,具体见图5所示。

图4 拉伸对标模型
针对CR180IF,缩颈前(工程应变<0.210),所有本构方程仿真计算的曲线与试验曲线吻合的非常好。缩颈后采用α=0.5仿真计算的曲线与试验曲线的吻合度要好于α=0.4和α=0.6。应变从0.2到0.36范围内,工程应力的试验值和仿真值对比见表3所示。通过拉伸试验和仿真计算获得的工程应力差值小于5.4 MPa,相对差值在1.6%以内,仿真计算能很好的吻合试验值。
针对CR260IF,缩颈前(工程应变<0.208),所有本构方程仿真计算的曲线与试验曲线吻合的非常好。缩颈后采用α=0.4仿真计算的曲线与试验曲线的吻合度要好于α=0.3和α=0.5。应变从0.2到0.36范围内,工程应力的试验值和仿真值对比见表4所示。通过拉伸试验和仿真计算获得的工程应力差值小于7 MPa,相对差值在2%以内,仿真计算能很好的吻合试验值。
7 结论
在拉伸试验过程中,当材料超过抗拉强度就会发生局部缩颈,因此缩颈后的应力-应变曲线并不能反映真实的应变强化,需要利用本构方程进行拟合外推。Swift本构方程拟合外推的曲线应变强化较大,而Hockett-Sherby本构方程拟合外推的曲线应变强化偏弱。针对高强IF钢CR180IF和CR260IF,采用Swift-Hockett-Sherby混合本构方程,通过加权不同的系数获得不同的应变强化。通过仿真对标,当加权系数分别为0.4、0.5时,CR180IF和CR260IF拉伸试验曲线和仿真计算曲线拟合最好。CR180IF从0.2到0.36范围内,通过拉伸试验和仿真计算获得的工程应力差值小于5.4 MPa,相对差值在2%以内;CR260IF从0.2到0.36范围内,通过拉伸试验和仿真计算获得的工程应力差值小于7 MPa,相对差值在2%以内。
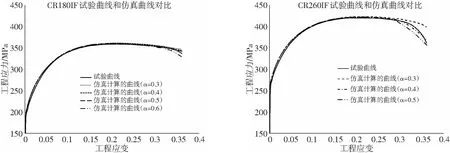
(1)CR180IF (2)CR260IF图5 高强IF钢试验曲线和仿真曲线对比
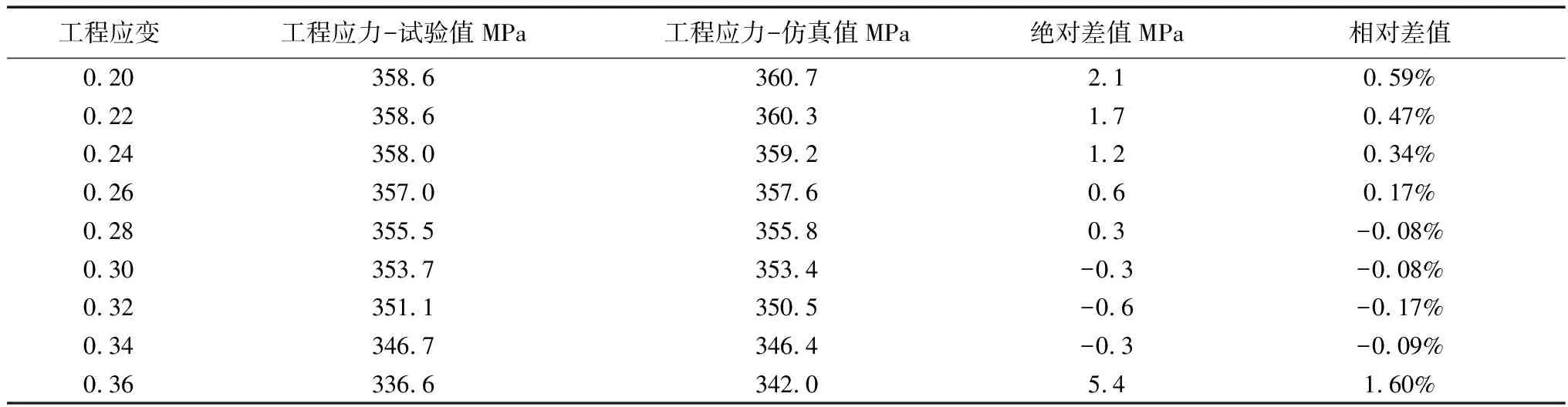
表3 CR180IF工程应力试验值与仿真值的对比
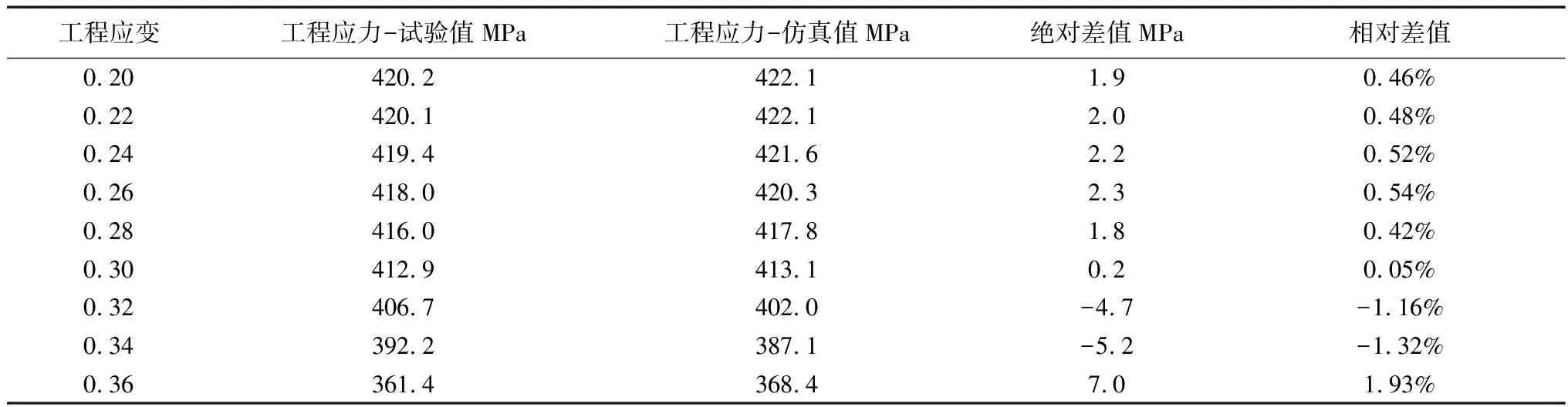
表4 CR260IF工程应力试验值与仿真值的对比
