Horadam多项式定义的两类双单叶解析 函数的系数估计

张成

（滁州城市职业学院 基础部，安徽 滁州 239000）

用R=(-∞,+∞)表示全体实数，C表示全体复数，用N:=｛1,2,3,...｝=N0{0}表示全体正整数. 令Α表示具有下述形式的函数的全体：

其在单位圆Δ={z:z∈C,|z|＜1}内解析. 用S表示Α中所有的单叶函数.

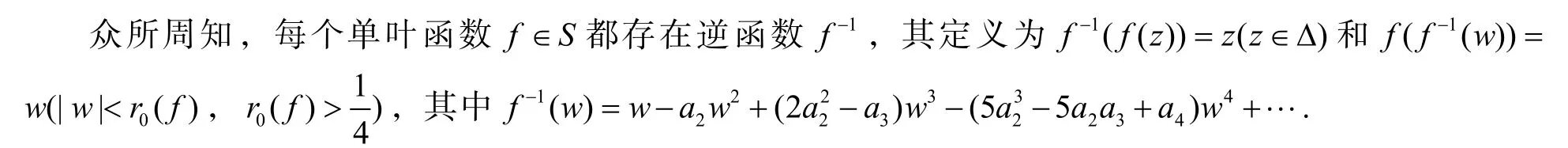
特别地，一个函数f∈Α称为Δ内的双单叶函数，如果函数f与其逆函数f-1都在Δ内是单叶函数. 用∑表示Δ的双单叶函数的全体.

根据文献[1-2]，Horadam多项式hn(x,a,b;p,q)记为hn(x)，满足下列递推公式：

当Horadam多项式hn(x)中的参数取一些特殊值时，就变为我们熟知的多项式：

其中，x∈R与z∈C是相互独立的，即x≠ℜ(z).

学者们研究了从属于多项式的双单叶解析函数类系数[3-10]，其中，文献[3]研究了函数类G∑(λ;x)和R∑γ,λ(x)的系数估计. 但既有研究在处理双单叶函数的系数估计时，考虑的限制条件少，其结果不够精确. 本文拟用文献[9]的方法，重新研究此函数类的系数，以期得到更精确的系数估计.

1 主要结果

定理1如果f(z)∈G∑(λ;x)，则：

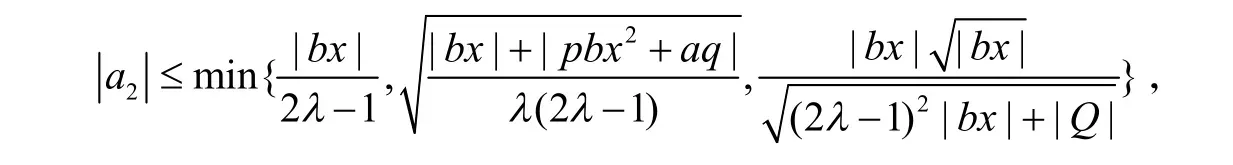
类似于定理1的证明，定理2得证.

注定理2要比文献[3]中的定理2.2更精确.

2 主要推论

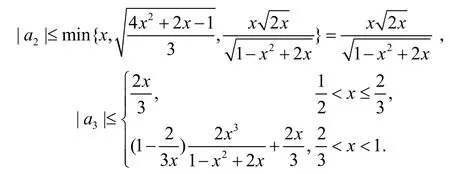
注推论3中|a2|、|a3|的估计要比文献[12]中的推论8更准确.