基于等效夹杂法的含多圆形夹杂的无限平面 热应力分析

黄云海，张炯，杨超，刘卫东

（1.五邑大学 土木建筑学院，广东 江门 529020；2.河海大学 机械学院，江苏 南京 210098）

颗粒增强复合材料具有优异的力学性能，在航空和机械等领域应用广泛. 然而，在其制造或使用过程中，由于热失配产生的残余应力会沿着夹杂物和基体之间的界面累积；当界面热应力与外荷载引起的应力结合时可能会引发界面裂纹，从而导致疲劳失效和材料性能下降. 因此，复合材料的界面热应力问题一直是人们关注的热点，研究者们采用了诸如复变函数、Mori-Tanaka方法和保角变换法等[1-4]探究了此类问题. 但从计算效率上讲，采用上述方法计算过程较为复杂，特别是处理多夹杂问题时效率较低.

从本质上讲，纤维可以被认为是嵌入在基体中的夹杂，Eshelby等效夹杂法[5-6]是研究纤维增强复合材料热应力的有效方法：Shibato[7]研究了由扁球形夹杂和基于等效夹杂方法的基体界定的错配界面引起的应力分布；Sanboh Lee[8]基于等效夹杂方法研究了球状夹杂引起的热应力. 一直以来，在采用等效夹杂法求解夹杂问题时，外弹性场的求解比较复杂. 然而，Jin[9]对于平面情形给出了Eshelby外部张量的封闭形式，这使得等效夹杂法更便于求解纤维增强复合材料的热应力，本文作者也在此基础上对无限大平面含单个夹杂的热应力进行了研究[10]. 然而实际工程中，复合材料会涉及到多个夹杂，为了解决无限平面含多个夹杂的热弹性场分布问题，本文同时采用Eshelby内部张量和Eshelby外部张量，将等效夹杂法的应用扩展到含多个圆形夹杂的无限大平面在均匀温度变化时热弹性场分布的场景.

1 等效夹杂法

对于图1和图2所示问题，根据胡克定律，可在任意夹杂Ii(i=1,2,…,n)中心建立平衡方程：

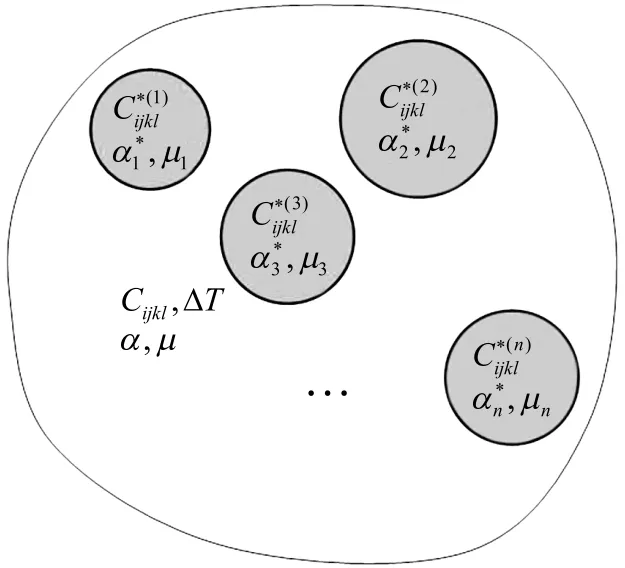
图1 均匀温度变化下无限大平面含任意个圆形夹杂

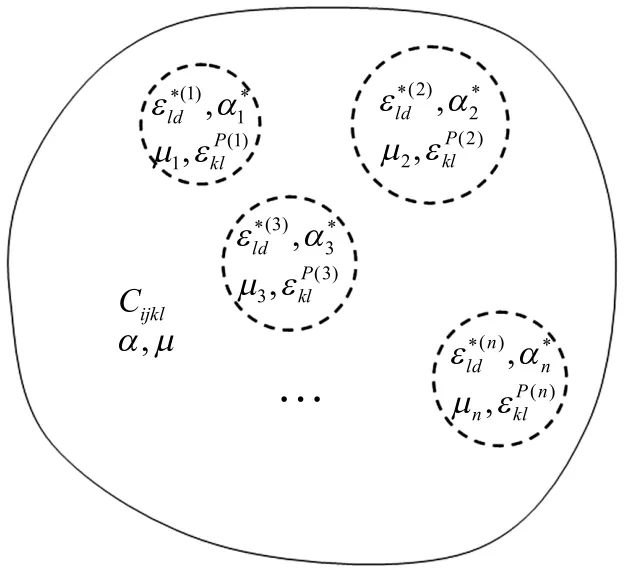
图2 等效夹杂法处理图1的结果

2 等效夹杂法求解的有效性分析

有限元法是求解偏微分方程边值问题近似解的数值技术，在固体力学领域得到了广泛的运用. 基于有限元解的准确性，其通常用来验证其他解法的准确性，如文献[11-12]均采用有限元法验证了其关于夹杂的弹性问题的理论解的正确性，因此本文结果也与有限元法进行对比.

将上述求解方法利用编程实现，并将本文方法的计算结果与ABAQUS的计算结果进行比较，以验证其有效性. 所有计算均在2.0 GHz的i5 CPU的电脑上进行. 本文算例均假设为平面应变问题.

如图3所示的一个无限大板含有2个圆形夹杂，基体与夹杂的材料参数如表1所示. 夹杂的半径分别为r1和r2，设r1=r2=1.0，两个夹杂之间的距离L=3.0；基体与2个夹杂的剪切模量分别为μ、μ1和μ2，令μ1=μ2，两夹杂圆心连线与x轴所成夹角为β，无限大板受到均匀的温度变化1.0TΔ=℃. 采用本文方法和有限元法计算了当45β=°时的Von Mises应力分布和S11应力分布，具体如图4和图5所示.

图3 无限大平面下含2个圆形夹杂

图5 S11应力云图（=45β °）

表1 基体与夹杂的材料参数

图4 Von Mises应力图（=45β °）

从图4～5可以看出，本文方法的计算结果与ABAQUS的计算结果吻合较好，两种方法的Von Mises应力和S11应力的最大误差分别在2%和2.5%内，证明了本文方法的准确性. 在计算图5所示的S11应力云图时，本文方法用时15.4 s，而有限元法用时94.8 s，表明本文方法具有更高的计算效率. 有限元法计算效率不如本文方法，原因是采用有限元求解时，必须对全局进行网格划分，且在夹杂界面处的网格划分尤为密集，而后需要同时求解；本文方法在求解该问题时，各点之间独立求解，并无直接联系.

3 多圆夹杂的无限平面热应力分析

由于夹杂物和基体之间的热膨胀系数不同，在温度变化时会产生热失配，由此引起的热应力和热变形是导致材料破坏的一个重要原因，因此研究夹杂物的排布方式和弹性常数对热弹性场的影响规律有着重要的现实意义. 下面采用本文方法，对无限大平面下含多个圆形夹杂的热弹性场进行计算，并分别求出夹杂界面的径向应力差值（rσΔ ）、环向应力差值（θσΔ ）、剪应力差值(rθσΔ).

3.1 夹杂排布方式对界面应力的影响

为了探究夹杂排布方式对界面热应力的影响，在无限大平面内不断加入不同数量的圆形夹杂，产生如图6所示的5种不同的夹杂排布方式：5个夹杂的菱形排布、3×3的方形布置、13个夹杂的菱形排布、5×5和7×7的方形布置. 每个圆形夹杂的半径R=1.0，间距L=3R. 基体和夹杂的材料参数如表2所示，且每个夹杂的弹性模量相同. 固定夹杂与基底的剪切模量比值K=μi/μ=2.0，其中μ=E/2(1+v)；ΔT=1.0℃；计算当无限大平面下分别含5、9、13、25、49个圆形夹杂时的界面应力差值变化情况.

表2 基体与夹杂的材料参数

图6 圆形夹杂布置

由于几何形状和温度变化的对称性，我们只计算了0°~45°处的界面热应力. 计算结果如图7所示：当采用3×3、5×5和7×7的方形排布时三个应力差值明显小于菱形排布，而采用5个夹杂的菱形布置时应力集中现象最为明显；当采用方形周期排布时，排布数量的增加对应力差值的影响不大，且在55× 处开始收敛.

3.2 剪切模量比对界面应力的影响

为了探究夹杂弹性常数对界面热应力的影响，以图7中55× 的方形排布为例，基体和夹杂的材料参数如表3所示，固定L=3R，每个圆形夹杂的半径均为R=1.0，ΔT=1℃，每个夹杂的弹性模量相同；计算夹杂与基底的剪切模量比值K分别取0.1,0.4,1.0,2.0,10.0和∞时的界面应力差值. 结果如图8所示：当采用方形排布时，应力差值呈对称性；且三个应力差值随着K的增加其增幅逐渐减少，并在K=10.0时开始收敛；环向应力差值受K的影响较大，而角度对其的影响较小，这可能与夹杂的几何形状有关；径向应力差值的峰值出现在45°处，而剪应力差值的峰值则出现在20°附近.

表3 基体与夹杂的材料参数

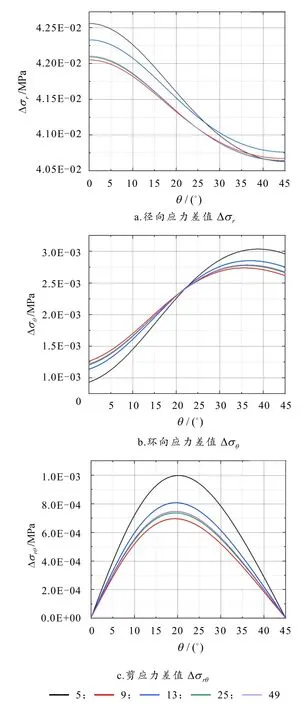
图7 不同夹杂排布方式下的界面应力差值

图8 不同K值下的界面应力差值

4 结论

本文基于等效夹杂法对无限平面含多夹杂的热弹性问题进行了理论推导和程序实现，通过有限元分析验证了方法的正确性和高效性，并探讨了夹杂排布方式和剪切模量比对界面热应力的影响，结果表明方形排布有利于降低界面应力差值，更适用于复合材料的生产. 此外，利用等效夹杂法计算含多个圆形夹杂结构的热弹性场，不需要像有限元方法一样对整个结构进行建模和网格划分，而只需要夹杂的位置、半径和弹性模量就可以进行计算，十分方便和高效，体现了该方法在复合材料细观力学分析中的实用性和有效性. 但是本文工作目前仅适用于二维情况，后续可进一步扩展到三维问题.