交超格上的模糊超滤子

赵雪欣，谢祥云

（1.五邑大学 数学与计算科学学院，广东 江门 529020； 2.江门职业技术学院 教育与教育技术系，广东 江门 529030）

1 引言及预备知识

1965年Zadeh首次提出模糊集的概念[1]，1971年Rosenfeld[2]探讨了模糊子群的概念，自那以后，模糊代数结构被广泛研究. Liu[3]探讨了模糊子环的概念，Kuroki[4]研究了模糊半群的相关性质，Yuan和Wu[5]探讨了格上的模糊理论等. 超结构理论最初是由Marty在1934年第八届数学家代表大会上提出的[6]. 随着超结构理论的发展，超代数系统理论被应用到很多方面. Koguep等[7]研究了超格上的模糊素理想；Hedayati[8]研究了超格上的模糊超滤子；Feng等研究了模糊子超格的直积和区间值模糊子超格[9]，以及(,)λμ-模糊子超格[10]；Xin等[11]研究了超格上的模糊软超理想等.

本文引入了交超格上的(∈,∈∨q)-模糊超滤子以及它与超滤子之间的等价刻画，给出模糊超滤子的概念以及等价刻画，并进一步探讨supp(μ)的等价刻画，以及χF的等价刻画.

定义1[6]设H是一个非空集合，H上的二元超运算是指f:H×H→P*(H)的一个映射，其中P*(H)表示H的所有非空子集的集合，P*(H)=P(H)-∅.

定义2[12]171设L是一个非空集合，在L上定义二元超运算“∧”和普通二元运算“∨”如下所示，如果对任意的a,b,c∈L，满足：

1）a∈a∧a，a=a∨a；

2）a∧b=b∧a，a∨b=b∨a；

3）(a∧b)∧c=a∧(b∧c)，(a∨b)∨c=a∨(b∨c)；

4）a∈[a∧(a∨b)]∩[a∨(a∧b)].

则L称为交超格.

若交超格L满足a∈a∧b⇒a∨b=b，则L称为强交超格. 其中对任意的A,B∈P*(L)，记A∧B=∪{a∧b a∈A, b∈B}，A∨B={a∨b a∈A, b∈B}，特别地，若A={a}，则A∧B记为a∧B.

由定义2，若a,b∈L且a∨b=b，则有a∈[a∧(a∨b)]∩[a∨(a∧b)]，因此a∈a∧(a∨b)=a∧b ，即a∨b=b⇔a∈a∧b.

在交超格L上定义二元关系“≤”：(∀a,b∈L) a≤b⇔a∨b=b，则“≤”是L上的一个偏序关系. 在(L,≤)中，若存在最小元，则记为0；若存在最大元，则记为1.

定义3[12]173交超格L上的一个非空子集F称为L上的一个超滤子，如果：

1）∀x,y∈F⇒x∧y⊆F；

2）∀x∈F,x≤y⇒y∈F .

定义4设μ是交超格L上的模糊子集，则μ是L上的一个模糊超滤子，如果对任意的x, y∈L：

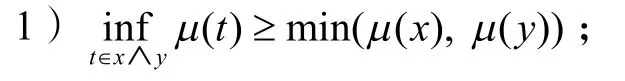
2）x≤y⇒μ(x)≤μ(y).

定理1 设μ是交超格L上的模糊子集，则μ是L上的一个模糊超滤子当且仅当对任意的α∈[0, 1]，μα(≠∅)是L上的一个超滤子.

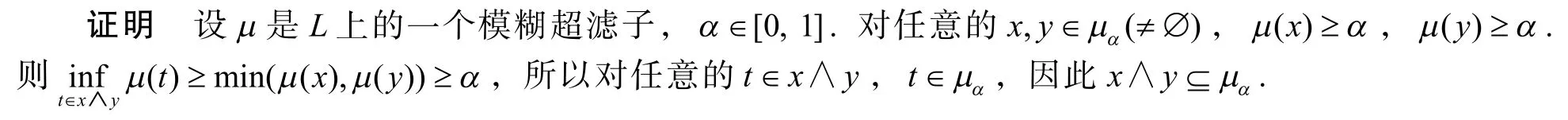
设x∈μα，x≤y，则有μ(y)≥μ(x)≥α，因此y∈μα，μα(≠∅)是L上的一个超滤子.

假设存在x0,y0∈L使得x0≤y0且α=μ(x0)＞μ(y0)，则x0∈μα，y0∉μα，矛盾. 因此对任意的x, y∈L，x≤y⇒μ(x)≤μ(y).

定义5设L1和L2是两个交超格，映射f:L1→L2称为同态，若对任意的x,y∈L满足：

1）f(x∨y)=f(x)∨f(y )；

2）f(x∧y)=f(x)∧f(y ).

由定义5的1）知，若x≤y，则f(y)=f(x∨y)=f(x)∨f(y )，所以f(x)≤f(y)，因此有x≤y⇒f(x)≤f(y)，即f是保序的.

2 主要结果

交超格L上的模糊子集μ形如

设L是一个交超格，x,y∈L，若对任意的t∈x∧y，有tr∈∨qμ(r∈[0,1])，即tr∈μ或trqμ，则记为(x∧y)r⊆∨qμ.

定义6设μ是交超格L上的一个模糊子集，μ称为L上的一个(∈,∈∨q)-模糊超滤子，如果对任意的r,s∈[0,1]和x,y∈L，有

i）xr,ys∈μ⇒(x∧y)min(r,s)⊆∨qμ；

ii）xr∈μ,x≤y⇒yr∈∨qμ.

特别地，由定义4，交超格L上的每一个模糊超滤子都是一个(∈,∈∨q)-模糊超滤子，反之不一定成立.

例1设L={0,a,b, 1}，定义L上的∧-超运算和∨-运算如下表1，则L是一个交超格.

表1 ∧-超运算和∨-运算的运算表

L上的模糊子集μ定义如下：

推论1交超格L上的一个模糊子集μ是L的一个(,)q∈∈-∨ 模糊超滤子当且仅当定理2中的1）和2）成立.

定理3设μ是交超格L上的一个模糊子集，若μ是L的一个(,)q∈∈-∨ 模糊超滤子，则对任意的00.5r≤ ≤ ，rμ=∅或rμ是L的一个超滤子；

反之，若对任意的0≤r≤0.5，μr(≠∅)是L的一个超滤子，则μ是L的一个(∈,∈∨q)-模糊超滤子.

设x∈μr，x≤y，则有μ(x)≥r，μ(y)≥min(μ(x), 0.5)≥min(r, 0.5)=r，即y∈μr. 因此μr是L的一个超滤子.

反之，设μ是L上的一个模糊子集使得对任意的0≤r≤0.5，μr(≠∅)是L的一个超滤子.若x,y∈L，有

设μ是交超格L上的一个模糊子集，J是r∈[0, 1]构成的集合使得μr=∅或μr是L的一个超滤子. 若J=[0, 1]，则由定理1，μ是L的一个模糊超滤子；若J=[0, 0.5]，则由定理3，μ是L的一个(∈,∈∨q)-模糊超滤子. 类似地，下面给出J=(0.5 , 1]的情况.