基于导向矢量修正的空间临近强干扰阻塞方法

田蕴琦，向龙凤，肖开奇，朱 磊

(电子信息控制重点实验室，四川 成都 610036)

0 引言

水声对抗场景中，敌方常发射大功率干扰信号以掩盖和压制目标信号，影响我方对目标的波达方向(direction of arrival, DOA)估计，特别是当干扰与目标存在于同一波束内时，目标谱峰可能完全淹没在干扰谱峰或算法产生的伪峰中[1-2]，因此估计弱目标前需要对强干扰信号进行抑制。干扰抑制方法主要分为两类：一类是在干扰方向产生零限的自适应波束形成技术[3]，但这类方法在处理主瓣内的空间临近干扰时存在副瓣电平增高、主波束变形及偏移等问题[4]，难以达到理想的目标估计效果；另一类是干扰阻塞法[5](jamming jam method, JJM)，其与MUSIC等特征分解类算法结合可以获得较高的分辨率，但存在空间谱基底起伏问题，阻塞空间临近强干扰时会对目标峰值造成衰减，甚至产生探测盲区。针对这一问题，文献[6]利用阵列协方差矩阵Toeplitz平均后的特点构造阻塞矩阵，减小了干扰抵消造成的信号衰减，但未解决空间谱基底起伏问题。文献[7]利用对角加载修正因子对阻塞处理后的协方差矩阵进行修正，减小了波束畸变和探测盲区，但在实际中存在对角加载电平不易选取的问题。文献[8]通过对导向矢量进行二次不等式约束，利用拉格朗日乘数法和牛顿迭代法求出了对角加载电平的精确值，但该算法对干扰估计误差要求较高。文献[9]采用多尺度形态学方法对干扰阻塞输出波束进行校正，降低了波束基底起伏，但该方法未从根本上解决波束基底起伏问题，且多次形态学处理引入了较大的计算量。

针对JJM在抑制空间临近强干扰时弱目标方位估计性能不佳的问题，本文提出基于导向矢量修正的干扰阻塞方法(jamming jam method based on modified steering vector, MSV-JJM)，通过导向矢量模值一致化约束，抵消阻塞处理对MUSIC空间谱的影响，提高弱目标的DOA估计性能。

1 干扰阻塞方法

干扰阻塞法的原理是利用干扰的方向信息构建一个阻塞变换矩阵，剔除掉阵列输出数据里的干扰信号。

x(t)=As(t)+n(t)

(1)

式(1)中，x(t)=[x1(t),x2(t),…,xM(t)]T为阵列数据；s(t)=[s1(t),s2(t),…,sK(t)]T为入射信号矢量；n(t)=[n1(t),n2(t),…,nM(t)]T为接收噪声矢量；A=[a(θ1),a(θ2),…,a(θK)]为ULA对入射信号的阵列流形矩阵，而a(θk)=[1,e-juk,e-j2uk,…,e-j(M-1)uk]T表示第k个信号的导向矢量，uk=2πdsinθk/λ，λ为信号波长。阵列接收数据的协方差矩阵为：

(2)

式(2)中，E[·]表示统计平均，Rs=E[s(t)sH(t)]，IM表示M×M维单位阵。

当强干扰信号s0(t)从θ0方向入射，干扰导向矢量为a(θ0)，JJM的阻塞变换矩阵如式(3)所示：

(3)

T左乘阵列接收数据，得到：

(4)

当θk=θ0时，干扰信号被从阵列接收数据中剔除掉，而其他方向的信号相比阻塞处理之前发生了1-e-j(uk-u0)倍的变化，y(t)降为(M-1)×1维向量，说明阻塞矩阵导致了阵列孔径的减小。

2 空间临近强干扰阻塞方法

2.1 空间谱基底起伏原因分析

阻塞处理后阵列接收数据协方差矩阵为：

Ry=E[y(t)yH(t)]=TRxTH=
TARsAHTH+σn2TTH

(5)

对Ry进行特征分解：

(6)

式(6)中，Σ=diag{λ1,λ2,…,λM-1}为Ry的特征值矩阵，并且按照由大到小进行排序。US表示K个大特征值对应的信号子空间，UN表示剩余小特征值对应的噪声子空间。

由于阻塞处理使信号的导向矢量发生了降维和1-e-j(uk-u0)倍的线性变化，因此MUSIC的搜索矢量为a(θ)的前M-1维：

(7)

(8)

根据式(8)中的谱峰搜索公式即可估计弱目标的DOA。

从式(5)可以看出，由于阻塞矩阵的影响，噪声协方差矩阵变为σn2TTH，相当于引入了色噪声。各阵元的噪声不再相互独立，由信号导向矢量张成的空间和噪声子空间不再严格正交，当干扰与目标方位临近时MUSIC算法将失效[10]。因此利用JJM抑制空间临近强干扰必须先对阻塞矩阵进行白化预处理，将噪声恢复为高斯白噪声。白化矩阵Q为[11]：

Q=(TTH)-1/2

(9)

白化处理后的阵列数据协方差矩阵为：

Rz=QRyQH=QTARsAHTHQH+σn2I

(10)

(11)

(12)

(13)

因为阻塞矩阵T为行满秩矩阵，所以TTH为非奇异矩阵，可以特征分解表示为：

TTH=EΠEH

(14)

2.2 基于导向矢量修正的干扰阻塞法

根据2.1可知，导向矢量模值的变化是空间谱基底起伏的原因，因此本文在阻塞处理后对模值进行一致化约束，消除导向矢量模值的影响。假设修正因子为c(θ)，约束条件：

(15)

解得：

(16)

修正后的导向矢量为：

(17)

(18)

3 仿真验证

3.1 有效性仿真

图1 导向矢量模值Fig.1 Modulus of steering vectors

图2 MUSIC、JJM与MSV-JJM的空间谱Fig.2 Spatial spectrum of MUSIC, JJM and MSV-JJM

3.2 弱目标估计性能仿真

为比较JJM和MSV-JJM的弱目标DOA估计性能，设计如下仿真实验。仿真条件：ULA的阵元数为11，阵元间距满足半波长条件，考虑JJM引起的阵列孔径损失，半功率点波束宽度约为10.2°；目标1从5°入射，目标2从-20°入射，0°方向有一非相干强干扰，信干比-40 dB。干扰与目标的角度差小于半功率点波束宽度的一半时，可以认为是空间临近干扰，因此0°干扰是目标1的空间临近干扰，是目标2的普通干扰。噪声为加性高斯白噪声，信噪比为-5 dB，快拍数为300，蒙特卡洛实验次数为500。利用弱目标检测概率和DOA估计的均方根误差(root mean square error, RMSE)来衡量算法的弱目标估计性能。采用谱峰搜索的方式估计目标信号的DOA，通过限定DOA估计偏差得到弱目标的检测概率，检测门限为半功率点波束宽度的一半，RMSE根据满足检测条件的DOA估计值进行计算。

3.2.1信噪比对弱目标估计性能的影响

改变信噪比，其他仿真条件不变，弱目标检测概率结果如图3所示，实线表示目标1，虚线表示目标2。

图3 弱目标检测概率随信噪比变化曲线Fig.3 Detection probability varies withsignal-to-noise ratios

由图3可知，随着信噪比的增大，JJM和MSV-JJM的检测概率逐渐增大，对目标2的检测能力均强于目标1，MSV-JJM对两个目标检测性能的差距小于JJM。对于空间临近强干扰影响下的目标1，0 dB以下的相同信噪比条件，MSV-JJM的检测概率大于JJM；当检测概率大于0.9时，JJM和MSV-JJM对应的信噪比分别为-5 dB和-10 dB，因此MSV-JJM的信噪比门限更低，在低信噪比下具有更好的检测性能。两种方法均有效检测时，目标1 DOA估计的RMSE如表1所示，可以看出两种算法的DOA估计精度随信噪比的增加逐渐变高，相同信噪比下MSV-JJM的RMSE小于JJM，估计精度高于JJM。

表1 不同信噪比下目标1的RMSE

3.2.2干扰角度对弱目标估计性能的影响

目标入射角不变，改变干扰的入射角，检测概率如图4所示。目标1与干扰始终处于一个主波束内，随着干扰角度的逐渐接近，JJM对目标1的检测概率明显下降，并且小于MSV-JJM对目标1的检测概率；检测强干扰主波束以外的目标2时，JJM与MSV-JJM都具有较强的检测能力，检测概率始终为1。图4和表2的仿真结果验证了MSV-JJM较现有JJM能估计与强干扰角度相差更小的弱目标，且精度更高，适用于空间临近强干扰场景。

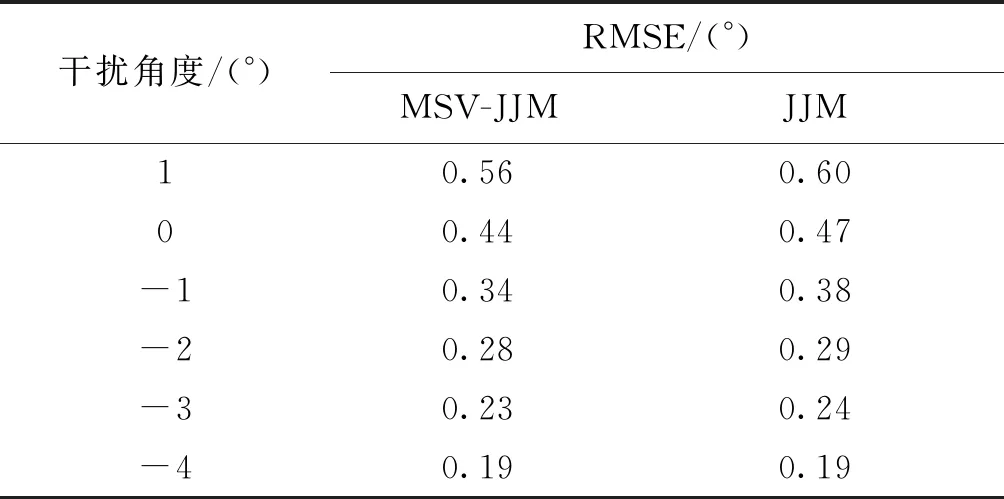
表2 不同干扰角度下目标1的RMSE

图4 弱目标检测概率随干扰角度变化曲线Fig.4 Detection probability varies withangles of the jamming

3.2.3阵元数对弱目标估计性能的影响

改变ULA的阵元数，检测门限随之动态调整，目标检测概率如图5所示，目标1的RMSE结果如表3所示。可以看出，随着阵元数的增加，JJM和MSV-JJM对目标1的检测概率逐渐增加，当检测概率大于0.9时，JJM和MSV-JJM对应的阵元数门限分别为11和8，相同阵元数下MSV-JJM的检测概率大于JJM，RMSE小于JJM。因此MSV-JJM相较于JJM，对阵元数的要求更低，估计精度更高。

表3 不同阵元数下目标1的RMSE

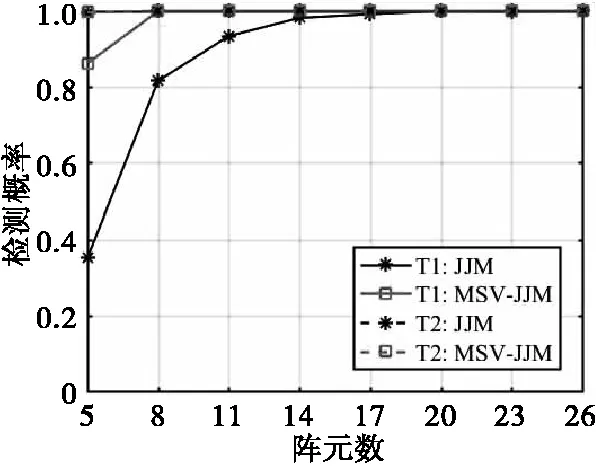
图5 弱目标检测概率随阵元数变化曲线Fig.5 Detection probability varies with number of elements

4 结论

本文提出基于导向矢量修正的空间临近强干扰阻塞方法。该方法首先根据强干扰方位信息构建阻塞矩阵，并对阻塞矩阵进行预白化，然后利用白化矩阵和阵列流形计算导向矢量模值修正因子，最后采用修正的导向矢量和阻塞后的阵列数据估计弱目标的方位。数值仿真表明：本文方法在阵元数为11，信噪比为-5 dB的条件下，可以有效检测与强干扰相邻1°，信干比-40 dB的弱目标；在信噪比较低、阵元数较少的情况下，弱目标DOA估计性能优于常规干扰阻塞法。因此，本文方法能够对主波束内的强干扰进行有效抑制，通过导向矢量模值一致化约束解决了阻塞处理引起的目标信号衰减和空间谱基底起伏问题，提高了干扰阻塞法对空间临近强干扰的适用性。