基于自适应MMSE-LSA与NMF的语音增强算法
2021-09-10马振中
董 胡,刘 刚,2,马振中
(1.长沙师范学院信息科学与工程学院,湖南 长沙 410100; 2.中南大学物理与电子学院,湖南 长沙 410012)
0 引言
语音增强是提高含噪语音信号质量和清晰度的重要步骤,为了更好地理解含噪语音信号,需要一种语音增强技术来去除环境中的噪声。在以往的文献中,各种各样的语音增强技术都被用于降噪。虽然抑制背景噪声和改善语音质量的语音增强算法的开发已经取得了一定的进展,但在提高语音清晰度和可懂度的算法方面仍需进一步改善。
近年来,相关研究者提出了一些低信噪比[1-2](<6 dB)环境下的语音增强算法。文献[3]提出基于单麦克风信道的语音增强算法,与传统的单通道语音增强方法相比,该算法具有较好的语音增强性能,但它不适用于快速变化的非平稳噪声。文献[4]和文献[5]分别提出基于波形网络、生成对抗网络的语音增强算法,这两种算法能较好地将目标语音与混合语音分离,但这两种算法的计算复杂度较高,对内存资源的要求较高。目前常用的谱减法、维纳滤波法、最小均方差估计法在去除背景噪声方面有一定的效果,但有时会造成语音失真或产生音乐噪声[6-8]。其中,幅度谱估计算法中的对数谱最小均方误差估计算法(minimum mean square error of log-spectral amplitude estimator, MMSE-LSA)[9-11]具有较好的语音保真度,因此得到广泛的关注;然而,传统MMSE-LSA算法无法依据输入信号的信噪比对增益因子作自适应调整,在输入信号的信噪比变化的条件下,该算法性能不稳定。非负矩阵分解(nonnegative matrix factorization, NMF) 算法对语音与噪声作非负矩阵分解获得相应字典矩阵,测试阶段将混合信号幅度谱分解为字典矩阵与权重矩阵的乘积;最后通过语音字典及权重矩阵乘积重构增强后语音[12-14]。本文针对上述问题,提出了基于自适应MMSE-LSA与NMF的语音增强算法。
1 自适应MMSE-LSA算法
MMSE-LSA算法对语音增强涉及先验信噪比与后验信噪比的估算问题[15]。伴随着对噪声估计结果的变化,需对信噪比作适时更新,由于在先验信噪比的估算过程中引入了调节因子α′,通常对其设定一个范围,再依据多次实验结果来确定一个经验值。然而,这种通过实验来确定经验值的方法,对于不同信噪比的情况可能会造成语音失真或产生音乐噪声问题,因此需对α′值作及时更新[8]。自适应MMSE-LSA算法则采用先验信噪比的最小均方差,依据噪声变化获得α′在不同信噪比情况下的自适应最优值。
x(n),d(n)和y(n)分别代表纯净语音、噪声及含噪语音,有:
y(n)=x(n)+d(n)
(1)
式(1)经FFT变换后可得下式:
|Y(n,k)|2=|X(n,k)|2+|D(n,k)|2
(2)
式(2)中,|Y(n,k)|2,|X(n,k)|2,|D(n,k)|2分别为含噪语音、纯净语音及噪声短时谱幅度。
Y(n,k)=|Y(n,k)|∠θy
(3)
X(n,k)=|X(n,k)|∠θx
(4)
式(3)、式(4)中,∠θx和∠θy代表相位。

(5)
|X(n,k)|=G(n,k)|Y(n,k)
(6)
(7)
式(7)中,ξ(n,k)为语音信号第n帧的第k个频率点先验信噪比,其定义如下:
(8)
(9)
从式(7)可知,计算增益函数须获得先验信噪比,进而才能估计出纯净语音,能否准确估计出先验信噪比对语音增强效果有重要影响。传统MMSE-LSA算法对先验信噪比的估计使用直接判决法。
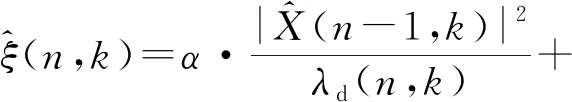
(10)
式(10)中,α依据经验其取值范围[0.8,1],ε为一个无限接近于0的正实数,γ(n,k)是后验信噪比(SNRpost(n,k)),定义如下:
(11)
由文献[16]可知,先验信噪比估计的另一种表示式为:
(12)

(13)
(14)
由式(12)和式(14)可得下式:
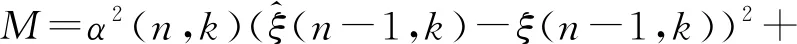
(15)
对M进行求导,并假定∂M/∂α[n,k]=0,则可求α的最优解:
(16)

2 NMF语音增强算法
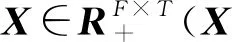
X≈WH
(17)
式(17)中,W为字典矩阵,K为W的维度,H为权重矩阵。W的列向量是描述X频谱结构的基向量,H中的值为W中基向量对应的激活值。式(17)可通过解决下面最优化问题获得W和H:
(18)
dKL(·|·)为广义Kullback-Leiber散度(KL divergence),定义为:
(19)
可通过下述乘法迭代准则得到最小化KL散度:
W=W.*((X./(WH))HT)./(lHT)
(20)
H=H.*(WT(X./(WH)))./(WTl)
(21)
其中,l为值全为1的矩阵,维度与X相同,.*和./表示矩阵逐点相乘和逐点相除。通过将W和H初始化为非负值,然后通过式(20)、式(21)迭代并更新W和H进而获得最终的W和H。基于NMF的语音增强算法主要由以下四个部分组成:
1) 计算训练数据中语音和噪声信号的幅度谱XS和XN、测试信号的幅度谱X;
2) 对XS和XN通过式(17)作非负矩阵分解,得到WS和WN,令W=[WS,WN];
3) 对X作非负矩阵分解,即X≈WH,固定W,由式(21)迭代获得权重矩阵H;
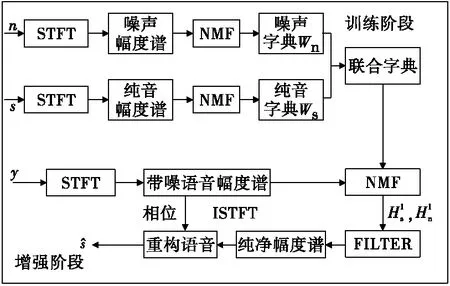
图1 NMF语音增强框架Fig.1 NMF speech enhancement framework
3 仿真实验结果
实验用的纯净语音来自于IEEE语音数据库,噪声选用Noisex-92噪声数据库。通过人工加噪方式,将纯净语音信号与噪声信号按一定信噪比进行混合(SNR=-5~10 dB),进而获得一定量的含噪语音信号,分别使用谱减算法、维纳滤波算法及本文提出的自适应MMSE-LSA与NMF算法进行语音增强,并将纯净语音信号作为评价增强效果的标准信号。选择语音质量感知评价(perceptual evaluation of speech quality, PESQ)[17]和对数谱距离(log-spectral distance, LSD)[18]作为语音增强效果的客观评价指标。
为了说明本文所提自适应MMSE-LSA与NMF语音增强算法的有效性,图2—图5分别给出white噪声、factory噪声、m109噪声及volvo噪声环境下SNR=-5 dB的含噪语音信号经谱减算法、维纳滤波算法及本文算法进行语音增强结果。从图2—图5可知,在-5 dB的white噪声、factory噪声、m109噪声及volvo噪声环境下,谱减算法的去噪效果相对于维纳滤波及本文提出的算法较差,对于语音中的清音部分几乎被噪声所掩盖;在低信噪比的factory噪声、m109噪声及volvo噪声环境下,谱减算法不仅无法有效提取语音中的清音部分,而且会产生语音失真及音乐噪声现象。在-5 dB的white噪声、factory噪声、m109噪声及volvo噪声环境下,维纳滤波算法相对谱减算法虽能较好地去除背景噪声,但维纳滤波算法无法提取出含噪语音中的清音部分,甚至将部分清音信号滤除掉,且会产生音乐噪声现象。本文算法与谱减算法、维纳滤波算法相比,不仅能准确有效地提取含噪语音中的清音部分,而且降低了音乐噪声,在可懂度和清晰度方面均具有较明显的优势。
实验对比分析了谱减算法、维纳滤波算法和本文提出的自适应MMSE-LSA与NMF语音增强算法在不同噪声环境下的语音增强效果,实验所得结果见表1与表2。表1给出了不同噪声环境下三种增强算法进行增强语音后的PESQ值,表2给出了对应的LSD值。

图2 含white噪声SNR=-5 dB谱减、维纳及本文算法增强结果Fig.2 Spectral subtraction, Wiener and enhancement results of our algorithm with SNR =-5 dB white noise

图3 含factory噪声SNR=-5 dB谱减、维纳及本文算法增强结果Fig.3 Spectral subtraction, Wiener and enhancement results of our algorithm with SNR =-5 dB factory noise

图4 含m109噪声SNR=-5 dB谱减、维纳及本文算法增强结果Fig.4 Spectral subtraction, Wiener and enhancement results of our algorithm with SNR =-5 dB m109 noise

图5 含volvo噪声SNR=-5 dB谱减、维纳及本文算法增强结果Fig.5 Spectral subtraction, Wiener and enhancement results of our algorithm with SNR =-5 dB volvo noise

表1 不同噪声环境下的PESQ
由表1可知,在white、factory、m109和volvo背景噪声环境下,当SNR分别为5、0和-5 dB时,本文提出算法的PESQ值要比谱减算法及维纳滤波算法高。
在SNR=-5 dB的white噪声及m109噪声环境下,本文所提算法的PESQ值最高比谱减算法分别高出0.503及0.403;在SNR=0 dB的white噪声及SNR=-5 dB的volvo噪声环境下,本文所提算法的PESQ值最高比维纳滤波算法分别高出0.174及0.147。

表2 不同噪声环境下的LSD
表2为在white、factory、m109及volvo噪声背景下,三种不同语音增强算法的LSD值。由表2可知,本文算法的LSD值均要小于谱减算法及维纳滤波算法,这主要是因为谱减算法及维纳滤波算法语音增强后存在“音乐噪声”,导致它们的LSD值相对较高。在给出的四种不同信噪比的噪声环境下,本文的语音增强算法的语音失真度都较小。在处于-5 dB的white噪声下,本文算法的LSD值相对于另外两种语音增强算法平均下降9.15%;在factory噪声下,LSD值平均下降 9.56%;在m109噪声下LSD值平均下降10.83%;volvo噪声下,LSD值平均下降12.12%。由此可见,低信噪的噪声环境下,本文提出的语音增强算法相对于谱减算法及维纳滤波算法,其LSD性能表现为最优。
4 结论
本文提出了基于自适应MMSE-LSA与NMF的语音增强算法。该算法结合了自适应对数谱幅度最小均方误差和非负矩阵分解两种语音增强算法的优点,利用MMSE估计器对含噪语音信号进行增强,提高输入信号的信噪比,然后利用NMF算法对增强后产生的语音失真和残留噪声进行补偿,既能有效地降低背景噪声又减少了语音失真。仿真实验结果表明,综合PESQ及LSD两种语音增强标准,本文提出的自适应MMSE-LSA与NMF语音增强算法要优于谱减算法及维纳滤波算法。此外,在不同的低信噪比环境下,语音增强算法具有良好的增强效果,表明本文提出的算法具有较强的适应能力。
