O2O模式下连锁超市生鲜百货的配送路径优化研究

何丹

摘  要：在新零售时代，传统连锁超市通过O2O模式进行零售变革，通过线上来挖掘和吸引客源，其关键在于配送的时效性、安全性、便捷性，而配送的一个重要环节便是配送路线的优化，寻找最优的配送路径，可以节省行驶的里程，提高配送效率，实现有效满足顾客的时间诉求。本文利用人本超市“淘鲜达”平台运营数据对其配送问题进行了描述，针对问题构建了带时间窗的配送路径优化模型，通过计算分析，该模型在解决其配送问题上有一定的可行性。

关键词：时间窗;配送路径;节约里程法

中图分类号：F721.7                              文献标识码：A               文章编号：1672-0105（2021）01-0047-06

A Research on Distribution Path Optimization of Fresh Department Store in Chain Supermarkets under O2O Mode

HE Dan

（Zhejiang Industry & Trade Vocational College， Wenzhou，325003，China）

Abstract：  In the era of new retail， traditional retail supermarket chain is changed to O2O Mode， which relies on online sources to explore and attract customers， and its key lies in the distribution of timeliness， safety， convenience. Moreover， an important part of delivery is to optimize distribution route， which means to search for an optimal distribution route， saving mileage， improving the efficiency of distribution and effectively meeting customers' demands. This paper describes the distribution problems of Renben Supermarket based on the operation data of “Tao Xianda” platform， and constructs a distribution path optimization model with time window to solve the problems. Through calculation and analysis， the model is feasible to solve the distribution problems.

Key Words：  time window;distribution path;saving algorithm

随着网络信息技术、云计算、大数据等数字技术的快速发展，零售新理念与新技术的融合正在加剧改变当前的零售业态。其中依托线下即时物流配送的B2C网上超市业务，逐渐发展成为一种新型的零售模式。这种新兴的O2O电子商务网购模式，随时随地连接线下商家与线上用户，有效地融合了线下实体经济与线上资源。传统连锁超市要借助O2O电子商务网购模式的优势，通过线上来挖掘和吸引客源，就需要解决最后一公里的配送问题。本文将利用浙江省人本超市“淘鲜达”运营数据对O2O模式下连锁超市物流配送问题展开研究，探索即时配送路径优化的方法。

一、问题描述

浙江人本超市有限公司正在借用“淘鲜达”平台的线上流量优势，推进线上线下的融合发展的路径。人本超市的客户可以通过“淘鲜达”平台下单，订单会自动分配到离客户最近的店面，由店面承担拣货配送任务，一般店面的配送范围大约3-5公里，但是客户对生鲜百货的消费订单，在商品准时送达方面要求比较高，因此，商品准时送达是提升线上流量的关键因素。课题组通过对新田园门店7月份的数据进行整理分析发现，该月客户订单取消率为16.60%，其中因配送超时的客户订单取消率为39.30%，同时客户订单超时送达率为20.12%。上午9：00-12：00，下午13：00-16：00，平均每個小时的客户订单达200单左右。客户需求是不确定，但是对时间是有要求的。针对客户需求不确定以及服务时间窗口限制，一般还要求每辆配送车辆从店面出发并最后再回到店面，进行下一单的配送，因此需要根据客户的位置、下订单时间、送达时间要求，进行安排配送任务。假设客户需求服从随机分布，根据这些特性，则构成了一种随机需求下带时间窗的物流即时配送路径问题。

二、基于时间窗的配送路径优化模型构建

在研究生鲜百货的配送车辆路径时，引入时间窗问题，综合考虑每一位消费者要求的服务时间、需求量以及门店与消费者之间的距离等因素，结合节约里程法，计算确定每一配送车辆的配送路线即服务各消费者的次序和时间，从而实现物流配送网络的优化。

节约里程法核心思想是根据节约里程大小依次将运输问题中的两个回路优化合并成为一个回路，每次路线优化合并后，其总运输距离减小的幅度达到最大程度，直到达到一辆车的装载限制时，再进行下一辆车的优化，逐步寻找最佳配送路线，实现高效率的配送，使配送的时间最小、距离最短、成本最低。

假设有节点集合[V={P0， P1， P2， P3 …， Pn}]，其中0为门店，1，2，3，4，…，n为客户节点。[Pn]的地理坐标为（[Xn， Yn]），[PnPn-1]表示节点[Pn]与[Pn-1]的距离（单位：公里），[Pn-n]表示[Pn]下的订单号，[Qj]表示第[j]个客户的订单量（包裹数），[Qi]表示的是第[i]条配送路线上所有客户的订单量（包裹数），[Si]表示第[i]条配送路线的最短距离（单位：公里）。

[mini=nSi]                                                               （1.1）

[s.t.]

[anPn-nbn]                                                       （1.2）

[an′tIbn′]                                                       （1.3）

[Qi=j=nQj8]                                                        （1.4）

[P0Pn4]                                                              （1.5）

[Si=j=nSj10]                                                      （1.6）

式（1.1）為模型的目标函数，即总配送距离最短。约束式（1.2）是指时间窗口（an，bn）的客户订单。约束式（1.3）为客户的服务时间窗口约束，保证客户在该时间窗口内得到服务。约束式（1.4）指第[i]条配送路线上的最大配送量，其值取自于公司运营经验设定值。约束式（1.5）是门店到客户间的距离约束，其值取自于公司运营经验设定值。约束式（1.6）第[i]条配送路线的最远距离约束，其值取自于公司运营经验设定值。

本配送路径优化模型在构建中，将时间窗问题和节约里程法进行了有效的融合，设定客户下单时间窗[[an，bn]]，从客户下订单的时间，选出本轮配送路线优化的订单[Pn-n];再设定客户服务时间窗[[an， bn]]，明确配送的距离、配送量，以总的配送距离最短为目标，利用节约里程法的公式进行计算，确定最优的配送路径。

三、实验

（一）示例构造

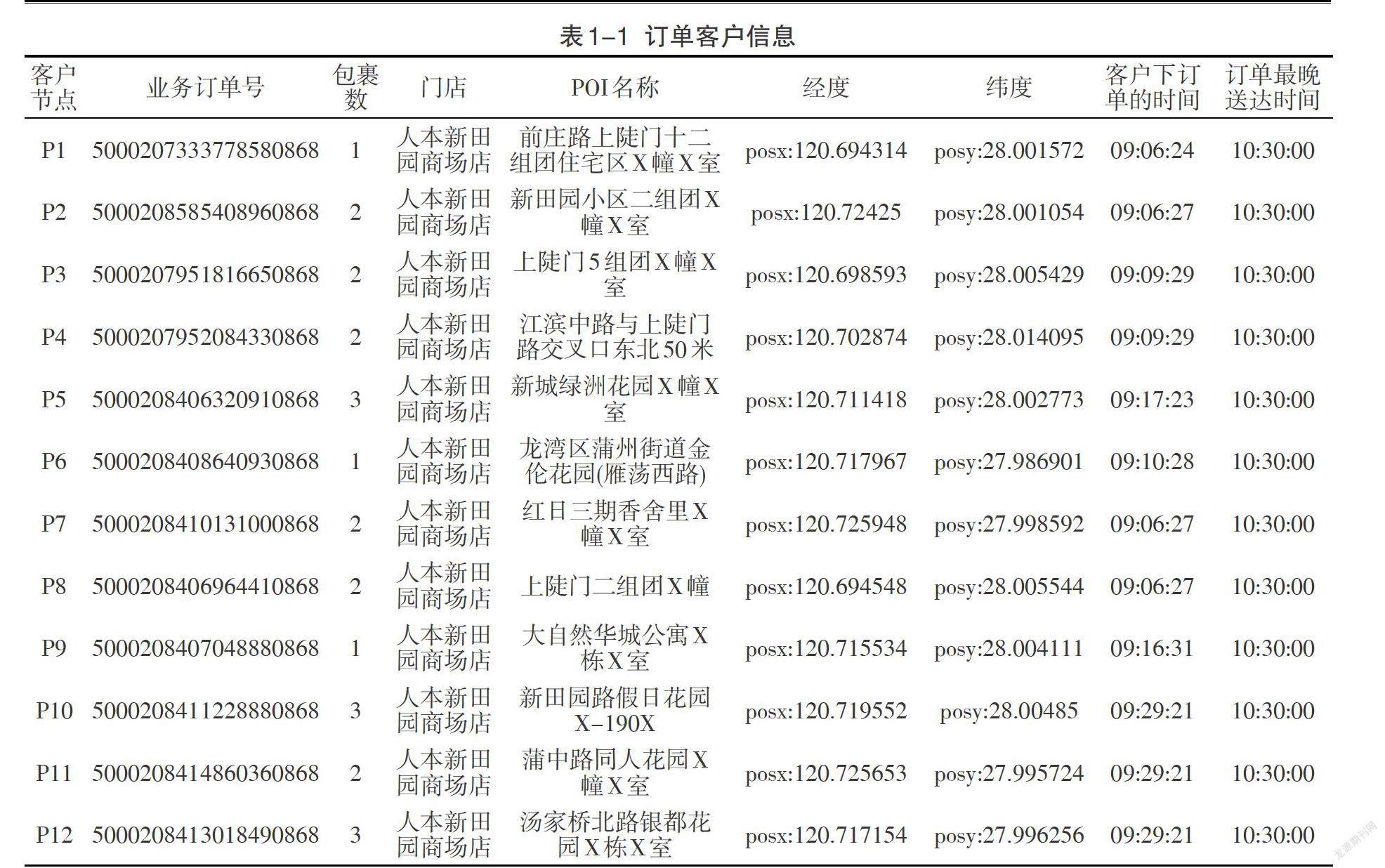
针对研究的问题，项目组随机从后台系统里挑选12客户进行基于时间窗口的节约里程法演算。查阅超市门店后台系统，时间窗口为9：00到9：30，这个时间区域的客户订单数为70单。随机挑选的订单，其客户的位置、包裹数、下单时间，送达时间要求，如下表1-1所示。

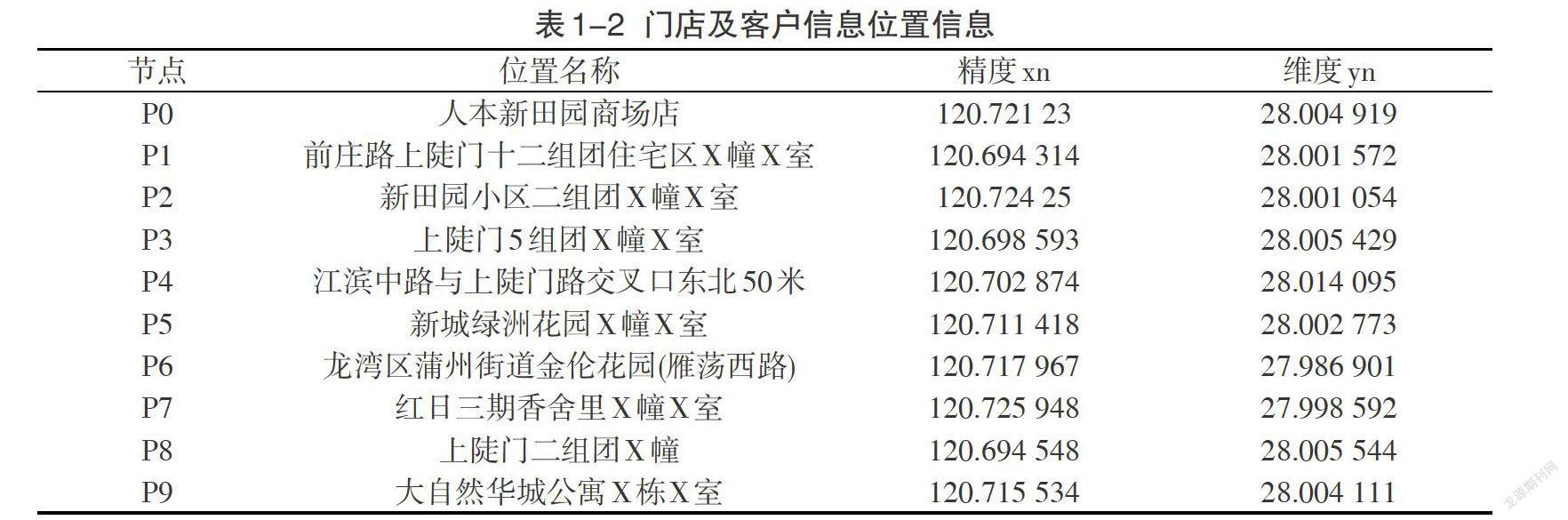
依据所构建的配送路径优化模型，对表1-1的数据进行整理。[P0]为人本新田园商场店，[P1， P2， P3…， P12]为12个客户，具体信息见表2-1。客户订单配送将由[P0]向[P1， P2， P3…， P12]等12个客户进行货物配送，送达时间范围要求为10：00—10：30。根据表1-3门店与客户以及客户间的最短骑行距离显示，12个客户都满足约束式（1.5），说明12个客户都是有效客户，因此，按照约束式（1.4）、（1.6），所规划配送路线的距离不能超过10公里，配载量不超过8件。在满足约束条件的基础上，实现配送距离最小化。

利用GPS软件，根据门店、客户的经纬度信息，计算门店与客户以及客户间的最短骑行距离，具体信息见表1-3。

（二）计算结果及分析

第一步：根据表1-3中门店与客户以及客户间的最短骑行距离，以[P0]為点，从[P1， P2， P3…， P12]中任意选择两个客户，形成三角形线路，按照两边之和大于第三边的原理，计算每条三角形线路的节约里程数，最后，其结果如表1-4所示。

第二步：将门店与客户间的节约里程按照从大到小的顺序进行排列，结果如表1-5所示。

第三步：根据模型中的约束条件与计算出的节约里程大小，按照顺序连接各客户节点，逐条进行配送线路的优化，其优化过程如下：

①原始解：从[P0]向[P1， P2， P3…， P12]等12个客户进行直达配送，能在时间窗口内完成配送任务，则配送线路为12条，其配送总距离[S=i=12Si=50.4]（公里）。

②节约里程优化：

第一，对第1条配送线路进行优化。按照节约里程排序大小，优先连接[P4-P8]，则配送线路为[P0-P4-P8-P0]。

第一次优化验证计算：

配送距离

[S1=j=4、8Sj =3.9+1.3+3.5=8.710]

配送量[Q1=j=4、8Qj=2+2=48]

第一次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接[P8-P1]，则配送线路优化为[P0-P4-P8-P1-P0]。

第二次优化验证计算：

配送距离

[S1=j=4、8、1Sj =3.9+1.3+0.97+3.2=9.3710]

配送量[Q1=j=4、8、1Qj=2+2+1=58]

第二次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接上[P3-P4]，则配送线路优化为[P0-P3-P4-P8-P1-P0]。

第三次优化验证计算：

配送距离

[S1=j=3、4、8、1Sj=2.7+1.3+1.3+0.97+3.2=9.4710]

配送量Q1=[j=3、4、8、1Qj]=2+2+1+2=7≤8

第三次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接上[P1-P6]，则配送线路优化为[P0-P3-P4-P8-P1-P6-P0]。

第四次优化验证计算：

配送距离

[S1=j=3、4、8、1、6Sj=2.7+1.3+1.3+0.97+3.7+3.4=13.37>10]

配送量Q1=[j=3、4、8、1、6Qj]=2+2+1+2+1=8≤8

第四次计算结果显示，配送距离超过10公里，配送量达最大值，故在该回路上不能连接上[P6]。因此，第1条最优配送线路为：[P0-P3-P4-P8-P1-P0]。

第二，对第2条配送线路进行优化。按照节约里程排序大小，接下来优先连接[P6-P11]，则配送线路为[P0-P6-P11-P0]。

第一次优化验证计算：

配送距离[S2=j=6、11Sj=3.4+1.7+2.1=7.210]

配送量[Q2=j=6、11Qj=1+2=38]

第一次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接[P12-P6]，则配送线路优化为[P0-P12-P6-P11-P0]。

第二次优化验证计算：

配送距离

[S2=j=12、6、11Sj=1.4+1.8+1.7+2.1=710]

配送量[Q2=j=12、6、11Qj=3+1+2=68]

第二次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接上[P11-P7]，则配送线路优化为[P0-P12-P6-P11-P7-P0]。

第三次优化验证计算：

配送距离

[S2=j=12、6、11、7Sj=1.4+1.8+1.7+0.85+1.4=7.1510]

配送量[Q2=j=12、6、11、7Qj=3+1+2+2=88]

第三次计算结果显示，配送距离虽未超过10公里，但配送量已达最大值，故在该回路上不能再继续连接。因此，第2条最优配送线路为：[P0-P3-P4-P8-P1-P0]。

第三，对第3条配送线路进行优化。按照节约里程排序大小，接下来优先连接[P5-P9]，则配送线路为[P0-P5-P9-P0]。

第一次优化验证计算：

配送距离[S3=j=5、9Sj=1.4+0.72+0.97=3.0910]

配送量[Q3=j=5、9Qj=3+1=48]

第一次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接[P2-P5]，则配送线路优化为[P0-P2-P5-P9-P0]。

第二次优化验证计算：

配送距离

[S3=j=2、5、9Sj=0.83+1.5+0.72+0.97=4.0210]

配送量[Q3=j=2、5、9Qj=2+3+1=68]

第二次计算结果显示，配送距离、配送量均未达到最佳值，故在该回路上可以继续连接。根据节约里程排序大小，再连接上[P10-P2]，则配送线路优化为[P0-P10-P2-P5-P9-P0]。

第三次优化验证计算：

配送距离

[S3=j=10、2、5、9Sj=0.39+0.82+1.5+0.72+0.97=4.410]

配送量[Q3=j=10、2、5、9Qj=2+2+3+1=88]

第三次计算结果显示，配送距离虽未超过10公里，但配送量已达最大值，故在该回路上不能再继续连接。因此，第3条最优配送线路为：[P0-P10-P2-P5-P9-P0]。

③优化结果汇总：

通过优化后，从[P0]向[P1， P2， P4…， P12]等12个客户进行配送，能在时间窗口内完成配送任务，可以通过3条配送线路来完成，其配送总距离[S=i=3Si=9.37+7.15+7.38=23.9]（公里），则总节约里程数[S=S-S50.4-23.9=26.5]（公里）。

四、结论

项目组构建的基于时间窗的节约里程法配送路径优化模型，通过随机抽取时间窗内的客户订单，根据节约里程法的原理进行计算分析发现，按照该模型进行配送路径优化，可以节约配送里程数达26.5公里，其节约里程数率达52.58%，说明该模型具有一定可行性。其节约里程的重要意义在于提高即时配送的效率，在一定程度上解决了客户需求不确定以及服务时间窗口限制等条件下的客户配送问题，有利于提升客户网络购物的体验以及满意度。后期项目组将按照该模型进行计算分析软件的开发，以便能更好地实现其价值。

参考文献：

[1] 刘威.基于B2C和O2O联合配送模式的车辆路径规划问题研究[D].广州：华南理工大学硕士学位论文，2018：26-38.

[2] 贺晶晶.O2O模式下连锁超市生鲜农产品物流配送路径优化研究[D].天津：天津理工大学硕士学位论文，2016：20-32.

[3] 李穗豫.基于电子商务农产品物流体系的构建研究[J].商场现代化，2008（03）：150-156.

[4] 王春兰.我国传统农产品流通模式问题及创新[J].价格月刊，2016（01）：73-76.

[5] 郭瑜等.O2O模式下连锁企业物流配送网络的路径优化[J].现代商贸工业，2020（27）：34-35.

（责任编辑：陈碎雷）