含孤石土质边坡稳定性及破坏特征的数值分析*
2021-09-09朱建旺赵炼恒胡世红
李 亮,朱建旺,赵炼恒,2,胡世红,左 仕
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙 410075)
0 引言
滑坡是最为常见也是最为严重的地质灾害之一。边坡力学性质复杂,内部受力状态易受外部环境(如降雨、荷载等)变化的影响,继而导致边坡失稳,滑坡每年都会造成大量的财产损失且严重危害人民群众的生命安全。通常的土质或岩质边坡,在进行稳定性分析时,可以将其视为均质材料,对于这类均质边坡,传统的基于假设滑裂面的条分法已经比较成熟。但在实际的工程应用中,经常遇到非均质材料组成的边坡,孤石边坡便是其中1种。
花岗岩不均匀风化形成的残留物被称为孤石(或称为花岗岩风化球),这种地质现象广泛分布于我国南部及东南的沿海地区,如福建和广州等地[1]。孤石的硬度大,形状不规则,而土体则较软弱,当孤石存在于边坡内部时,土石之间的不同力学性质容易使边坡内部软硬不均[2],复杂的内部构造和力学性质使得孤石边坡的潜在滑裂面形状复杂且难以事先估量,因此,传统的条分法难以适用,而有限元强度折减法既不需要假设滑裂面,又能计算边坡的应力、应变及位移场分布等内容[3],在复杂边坡计算方面的应用越来越广泛。
目前对孤石的研究主要侧重于2个方面,一是对孤石边坡安全性的研究,这一研究主要侧重于对边坡外露孤石的安全性分析,刘治军等[1]对不同存在形式的孤石根据特点分类,并建立力学模型计算,进行稳定性分析;杜甫志等[2]对孤石的分布进行合理划分,分析了孤石含量对土压力及边坡稳定性的影响。二是地下工程中孤石的探测研究,李术才等[4]提出了将地面物探普查方法和电阻率CT详查相结合的方法用来探测地铁盾构区间内的孤石;Cao等[5]分析了我国华南地区含孤石地区盾构施工过程中的盾构机选型和参数控制。
由此可见,现有对孤石地质的研究大多集中在孤石地下探测、盾构施工工艺优化、边坡外露孤石滚落等方面。然而对于通过勘查等手段探测出的边坡体内部的孤石形态对边坡稳定性影响的研究较少,刘晓华等[6]虽然利用FLAC3D软件,对孤石位置和角度对边坡安全性影响做了分析,但仅仅是二维分析。本文通过摄影测量技术和数字图像处理技术,对大量的野外孤石进行影像重构,建立了大量的孤石三维模型,以及具有不同形态孤石的边坡模型,并利用ABAQUS有限元软件对其进行计算,分析边坡内部孤石位置、大小和形状对边坡稳定性及破坏特征的影响。
1 孤石模型的建立
1.1 摄影测量原理
为了建立具有真实形状的孤石模型,本文采用摄影测量方法,对野外大量的孤石进行拍照,利用数字图像处理技术,建立孤石模型。摄影测量是通过摄像机获取被测量物体的二维信息,通过二维信息获取物体包括位置、大小和形状在内的三维信息的技术。进行测量时,首先要获取孤石的大量的二维信息,然后根据所获得的二维信息进行三维影像重构[7]。为了确保建立模型的精确,从不同角度对孤石进行拍照,并保证每次拍照的照片重叠率不低于60%。保证孤石上的每一个点都被捕获到。孤石三维影像重构依赖于二维影像,主要包括3个步骤:点云采集、点云处理和三角网格重建。首先从所有的2D图像中获取稀疏点云,点云中包含孤石表面的大量信息,图像中重叠的部分会自动校准重叠;之后利用基于多视点的立体视觉算法[8]对稀疏点云进行处理,获得密集点云,密集点云中含有孤石形态的细节信息;再根据所获得的密集点云,进行三角网格重构,从而获得完整的孤石模型。
1.2 孤石模型的处理
通过摄影测量技术和数字图像处理技术获得的孤石模型会被保存成由众多三角面片组成的.stl格式的模型文件。这些模型与真实块石的形状几乎一模一样,但模型精度越高,其形状越复杂,运算量就越大,计算时间就越长。为了减小运算量,在保证精度的情况下,对模型的三角面片进行简化,简化后的模型大约由300个三角面片组成,并将简化后的模型输出为可导入ABAQUS的.igs格式文件,整个块石模型的处理过程如图1所示。

图1 孤石模型
2 边坡模型的建立
本文探究孤石的位置,大小和形状对边坡稳定性的影响,基本思路是:1)首先从所建立大量孤石模型中随机选取5个具有不同形状参数的模型(如图2所示),作为平行试验,每个孤石模型分别置于均质边坡滑裂面的上部、中部和坡脚处,并对处于上部和中部的孤石模型向边坡坡面处平移,平移间距为1 m/次,改变其在边坡中的相对位置,分析孤石位置对边坡稳定性的影响;2)对1)中所选的孤石进行缩放,并将其置于滑裂面中部,探究孤石大小对边坡稳定性的影响;3)从建立的大量的孤石模型中,选取具有不同长细度和扁平度的模型,每组5个,探究孤石形状对边坡稳定性的影响。边坡模型尺寸如图3所示,本文共建立了181个边坡模型,如图4所示,其中均质边坡模型1个,内含孤石的边坡模型180个。

图2 5个不同形状的孤石模型

图3 模型尺寸
图4 边坡模型示意
3 模型边坡稳定性分析
3.1 强度折减法原理
有限元强度折减法最早由Zienkiewicz等[9]于1975年提出,其实现过程如式(1),在保持外荷载不变的情况下,用强度折减系数Fr对土体的黏聚力c和内摩擦角φ进行折减,将折减后的土体参数cm,φm代入有限元进行试算分析,随着折减系数的增大,土体材料的抗剪强度逐渐减弱,当土体因抗剪强度不足而达到极限状态时的Fr即为边坡安全系数。
(1)
3.2 模型信息
ABAQUS是目前最主流的应用于岩土非线性计算的软件之一。在ABAQUS中,将土体的黏聚力c和内摩擦角φ设置为随场变量线性变化,可以在计算中实现强度折减,为了使边坡不在计算第1个分析步时发生破坏,起始折减系数设置为0.5,终止折减系数设置为2,材料参数随场变量变化情况见表1。花岗岩风化土受岩性、环境条件和地理位置的影响,强度指标会有所不同,而相对于土体而言,孤石的强度又远大于土体,因此,结合相关工程经验,材料参数确定见表2。由于模型中土石的刚度差异大,且在具体的分析过程中,土-石接触面可能存在相对的滑移、分离等情况,因此,在模型土-石界面应设置合理接触类型。通用接触是ABAQUS中内置的1种接触类型,它可以自动搜索包括同一部件本身以及不同部件之间可能会相互接触的作用面,并赋予相应的接触参数,在接触面较多或者接触面形状复杂的模型中,具有良好的适用性。本文的土-石界面采用通用接触类型,其中在界面法向采用硬接触,即界面不可相互侵入,界面的切向采用罚函数来设置界面摩擦力,摩擦系数为0.5。

表1 随场变量变化的材料参数

表2 材料参数
3.3 模型安全系数的确定
运用有限单元法进行边坡稳定性分析时,对边坡失稳破坏时的判断准则讨论,目前主要有3种说法:一是将数值计算是否收敛作为边坡是否破坏的依据[10];二是将边坡特征点的位移发生突变作为边坡极限状态的判断依据[11];三是将塑性应变区的贯通作为边坡失稳判断准则[12]。在进行孤石边坡的强度折减分析时,当数值计算不收敛时,坡顶处此时已经发生无穷大的位移,此时的边坡实际上已经破坏,据此得出的安全系数一般偏大,而含孤石的边坡模型的塑性应变发展过程较为复杂,会出现塑性应变区不贯通的情况,因此,塑性应变区贯通也不适宜作为边坡失稳的判断依据。结合以上分析,本文采用坡顶处水平位移突变作为边坡失稳的判断依据。
4 结果分析
将建立的孤石边坡模型导入ABAQUS软件进行计算,并将计算结果加以分析,分析内容包含孤石对边坡安全系数的影响,对边坡位移的影响,对塑性应变发展的影响。
4.1 安全系数
4.1.1 孤石位置对边坡稳定性的影响
孤石的不同位置,会对边坡的稳定性造成不同的影响,本文利用5个不同形状和大小的孤石模型,分别将孤石中心置于滑裂面的上部、中部和坡脚处,并对上部的孤石向坡面处分别移动1,2,3,4,5,6,7 m,对中部的孤石向坡面分别移动1,2,3,4,5 m,坡脚处的孤石中心位于边坡内部的同一点,分别对这75个模型进行计算,分析孤石位置对边坡稳定性的影响,孤石模型中心位置如图5所示,计算结果见表3和图6。

图5 孤石中心点位置示意

表3 孤石位于坡脚处时边坡安全系数

图6 孤石位置对边坡安全系数的影响
如表3和图6所示,孤石的位置不同,孤石对边坡安全系数的影响不同,总体来说:
1)当孤石中心位于坡中时,随着孤石逐渐远离潜在滑裂面,边坡的安全系数逐渐减小,这是因为,当孤石中心位于滑裂面时,孤石对位于其上的土体的下滑趋势具有阻挡作用,从而增加了滑裂面的抗剪强度,使得安全系数提高,当孤石中心逐渐远离滑裂面,孤石对滑坡体的阻挡作用减弱,同时,由于孤石密度较土体大,滑坡体的下滑力增加,安全系数减小。
2)当孤石位于坡顶时,随着孤石位置逐渐远离均质边坡的滑裂面,边坡的安全系数出现先增大后减小的情况,这是因为,孤石的位置会改变边坡滑裂面的位置,孤石处于不同的位置,其对边坡滑裂面位置的改变效果不同,坡顶处的孤石更容易使均质边坡的潜在滑裂面位置改变。当孤石置于均质土坡滑裂面顶部时,由于孤石的存在,滑裂面会从孤石临近坡面一侧绕过,孤石起不到阻挡作用,随着孤石逐渐向坡面移动,边坡的滑裂面逐渐与孤石相交并出现绕石效应,故安全系数增大,当孤石进一步移动,孤石远离滑裂面,安全系数减小。
3)当孤石位于坡底时,相当于在坡底进行了加固,故相较于均质边坡,孤石边坡的安全系数增大。
4.1.2 孤石大小和形状对边坡稳定性的影响
描述三维颗粒形态的指标主要有长细度、扁平度、球度、平均半径、凸度、圆度、规则度和粗糙度等[7,13],其中长细度和扁平度、球度和平均半径是第1层次描述颗粒形态的指标,主要描述颗粒的宏观形状;凸度和圆度是第2层次描述颗粒形态的指标,用来描述颗粒表面的微观形貌;规则度和粗糙度是第3层次描述颗粒形态的指标,用来描述颗粒轮廓的纹理结构。本文利用平均半径(r)来描述孤石的大小,用长细度(EI)和扁平度(FI)来描述孤石的形状。平均半径定义为与孤石体积相等的等效球体的半径,见公式(2)。采用长细度(EI)和扁平度(FI)作为衡量孤石形状的指标,长细度和扁平度是Krumbein[14]提出的第1层次评价颗粒几何形状特性的指标,Krumbein认为颗粒的几何形状可以用颗粒沿3个主轴方向的轴长之比表示,其中3个主轴如图7所示[7],分别为,第1主轴(L)为颗粒最长方向的轴长;第2主轴(I)为垂直于L方向的次长轴的轴长;第3主轴(S)为同时垂直于L和I方向所测得的最短轴的轴长,EI和FI定义见公式(3)。

图7 颗粒3个主轴示意
(2)
式中:r为孤石平均半径,m;V为孤石体积,m3。
(3)
曹权等[15]对深圳市的孤石地质区进行钻孔探测,结果显示大部分孤石的竖向直径在0~5 m,超过5 m的只占4%。分析孤石平均半径为1,1.5,2,2.5,3 m和平均半径为2.5 m,EI,FI分别等于0.4,0.6,0.8,1.0时的边坡安全系数,孤石通过潜在滑裂面的中部,结果如图8~9所示。

图8 不同粒径孤石边坡安全系数
图8是对5个不同形状的孤石边坡模型,通过对孤石进行缩放至指定粒径,计算出的孤石通过潜在滑裂面中部时的安全系数。从图8中可以看出,随着孤石粒径的增大,边坡的安全系数逐渐增大,这是由于随着孤石粒径的增加,孤石对其上土体下滑的阻挡作用和影响范围也增大。相对孤石粒径而言,孤石形状对边坡稳定性的影响规律性较小,图9所示的为孤石长细度和扁平度分别为0.4,0.6,0.8,1.0组合时的孤石边坡的安全系数,每1组由5个具有相同EI和FI的不同孤石组成,共计80个模型,从图中可以看出,计算所得的安全系数均在1.40~1.49之间,而在每种组合下,安全系数的极差和变化幅度均较大,孤石形状对边坡安全系数的影响表现出不确定性。

图9 不同形状的孤石边坡安全系数
4.2 边坡破坏特征分析
就边坡土体在进行强度折减过程中的塑性应变发展过程及最终形成的虚拟位移分布2个方面来探讨孤石边坡破坏特征的影响。
图10、图11分别显示了典型的孤石边坡的塑性应变发展过程及虚拟位移场分布情况。具体可以看出,在孤石边坡内部抗剪强度逐渐折减的过程中,最先在土-石界面处发生破坏,塑性应变区最先在孤石周围发展,然后坡脚处也出现破坏,并延伸至土-石界面处,随后塑性应变进一步向坡顶发展至贯通,但随着土体强度的进一步折减,孤石周围的塑性应变值进一步发展,已贯通的塑性应变区逐渐收敛,最终的塑性应变区表现为1条以孤石周围为中心的极为不规则的塑性剪切应变带。整体来看,塑性应变最先出现在孤石周围的土体中,最终也是孤石周围的土体中的塑性应变最大,因此,在实际工程中,对于稳定性不高的孤石边坡,要特别注意对孤石的加固处理,防止因降雨等因素使孤石松动,进而导致灾害的发生。
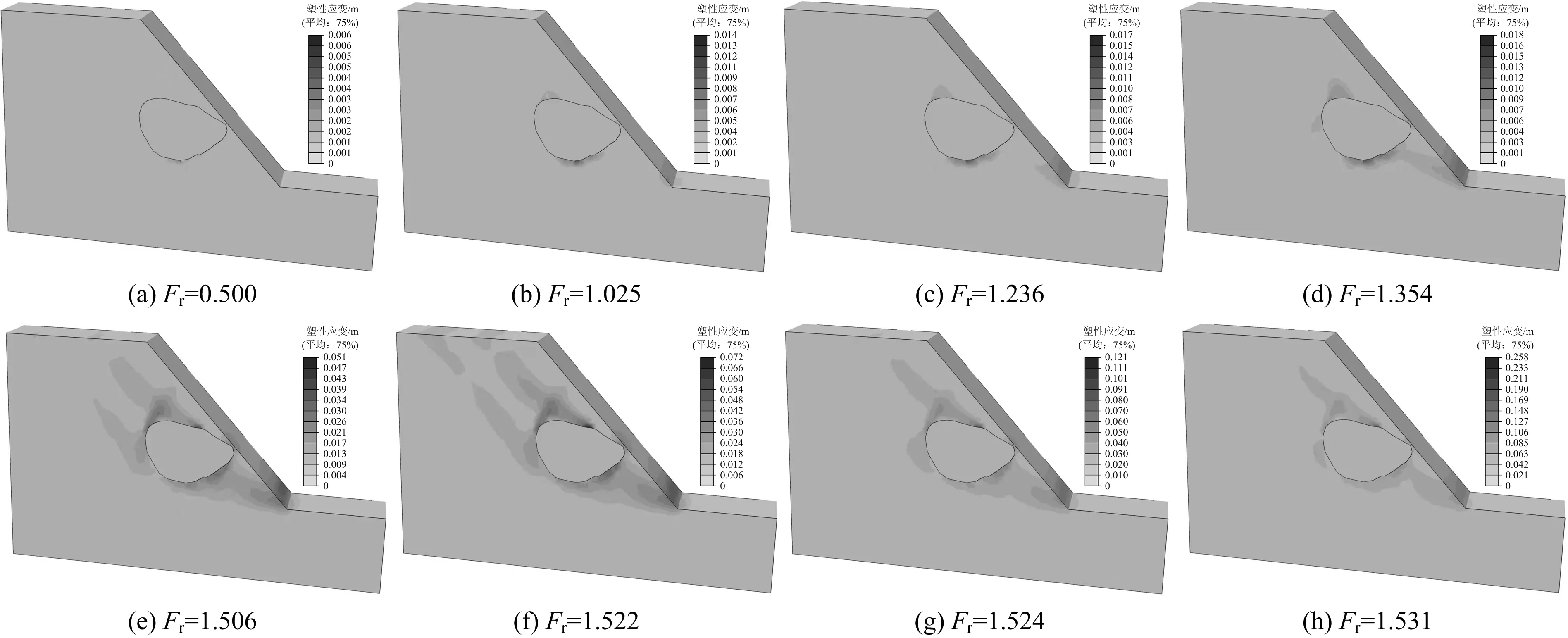
图10 孤石边坡塑性应变典型发展过程

图11 不同粒径孤石边坡位移
从最终的位移云图来看,不同位置、大小和形状的孤石对边坡的位移场分布情况有所不同,但又有一定的规律。就孤石大小而言,孤石的体积较小时,孤石对其上方土体几乎没有阻挡作用,甚至会增加下滑力,所以安全系数较小,随着孤石体积的增大,阻挡作用增大,安全系数增大,对位移场分布的影响逐渐增大。就位置而言,孤石会影响最大位移等值线的位置,不同位置的孤石,越靠近滑裂面,对最大位移等值面位置的改变越明显。另一方面,在距离边坡潜在滑裂面附近孤石,无论其形状大小如何,都会明显改变边坡最大位移向零位移转变的位移过渡区,使得位移过渡区范围增大,这个范围长度大致为孤石所在位置及其沿滑裂面方向向上至坡顶处,且范围宽度大致是整个孤石的宽度范围,孤石对土体的下滑的阻挡作用也体现在这一区域。
5 结论
1)孤石的位置和大小均会对边坡的稳定性产生规律性影响,具体表现为孤石位于坡底部时,边坡的安全系数会增加;当孤石位于坡中部时,随着孤石逐渐向坡面一侧远离滑裂面,边坡的安全系数逐渐降低;当孤石位于坡顶部时,随着孤石从潜在滑裂面逐渐向坡面侧远离,边坡的安全系数先增大后减小。孤石通过滑裂面中部时,孤石粒径越大,边坡安全系数越大。粒径相同时,孤石形状对边坡安全系数的影响表现出不确定性。
2)孤石对边坡安全系数的影响是通过改变滑裂面的位置和形状实现的。由于孤石的硬度和刚度远大于土体,在土体参数折减的过程中,塑性应变区和位移均会绕过孤石,形成绕石效应,从而改变滑裂面的位置和形状。
3)孤石影响了边坡塑性应变区的发展过程和位移场的分布情况。孤石边坡的塑性应变区发展以孤石为中心,向坡脚和坡顶发展,且最终的塑性应变区主要分布在孤石周围,最大塑性应变值也在孤石周围。孤石能减小其上方土体的位移值,使得边坡最大位移值向零位移值的过渡区范围增大,孤石的位置越靠近中部,孤石粒径越大,对位移场分布的影响越明显。
