不中断交通高速公路改扩建交通仿真参数标定
2021-09-09陈雅楠李美玲马晓刚
陈雅楠, 修 辉, 李美玲, 冉 晋, 马晓刚
(1.山东建筑大学 山东高校重点实验室道路与交通工程实验室, 济南 250101; 2.山东省交通科学研究院, 济南 250102; 3.山东高速股份有限公司, 济南 250101)
随着区域经济的快速发展和汽车保有量的迅速增长,先期建成的高速公路有很多已近饱和状态,通行效率下降严重,亟需改造提升。高速公路改扩建是一种很重要的改造方式,此类公路多为超大中修期服役,受数据采集设备和调查工具局限,较难得到改扩建道路持续真实的运行状态,借助仿真手段搭建微观交通模型[1]。近些年,PTV研发的VISSIM软件在道路交通研究领域广泛应用,但其中大量的独立参数显现的是德国交通系统特征,并不符合我国道路的实际情况,因此模型缺省值参数的标定工作对于特定工程的研究是必要的。
交通仿真参数标定主要有宏观参数校正法和全微观参数校正法,前者改变模型参数的输入值,以缩小宏观数值与实测值误差;后者利用加速度、车头时距、停车间距等实测微观数据校正[2]。涉及到的标定参数集各自取值范围庞大且无交集,国内外学者通过提高寻优效率的算法进行全局枚举工作。如孙剑等[3]以城市信号灯控交叉口为例,建立遗传模拟退火启发式算法,实现仿真参数的自动化校正;章玉等[4]发现模型标定时SPSA算法比GA算法快1.7倍;韩国华等[5]基于PSO算法提出完整校正流程;杨艳芳等[6]验证了SOGA算法应用;还有一些学者着力于改进遗传算法,进一步提高精确性和计算速度[7]。以上大多是针对复杂城市道路网系统进行的研究,由于不同场景交通流特性的差异,对于高速公路改扩建工程的参数标定还需进一步探讨。
参数标定的实质是不断调整微观交通仿真模型缺省值,选取模型输出结果与实测值误差最小的校核指标和参数,使标定后的仿真模型与道路实际运行状况更为接近。本文基于不中断交通高速公路 “双侧加宽”形式的仿真模型,研究指标参数取值与标定方法改进。标定好的模型能更好地呈现改扩建期间交通运行状况,可应用于济青高速后续相关问题的仿真研究,为今后类似的改扩建工程项目仿真参数标定提供参考依据。
1 交通仿真参数标定流程
改扩建期间因“边通车、边施工”,难以获得大量准确的微观实测数据,故应用现有的参数校正体系[8],参考周晨静等[9]有关全局参数敏感性分析的研究,依据微观交通仿真试验自身特性和方差分析理论,降低标定工作的复杂度。具体标定流程如下:
1) 提出高速公路改扩建工程模型驾驶参数选取依据,采集相关数据;
2) 对待标定指标和参数组合进行敏感性分析,检验各参数变化对模型运行结果的影响程度,筛选出对交通运行状况具有较大影响的重要指标和参数集,以简化标定工作量;
3) 设计交通仿真方案。利用科学有效的正交表格安排分析多因素、多水平的交通仿真试验,模拟验证具有代表性的参数水平组合,分析并评价仿真运行结果以全面了解目标问题,找出具备均匀分散、齐整可比的最优水平组合,作为不中断交通的高速公路改扩建工程模型参数标定方案[9-10],如图1所示。
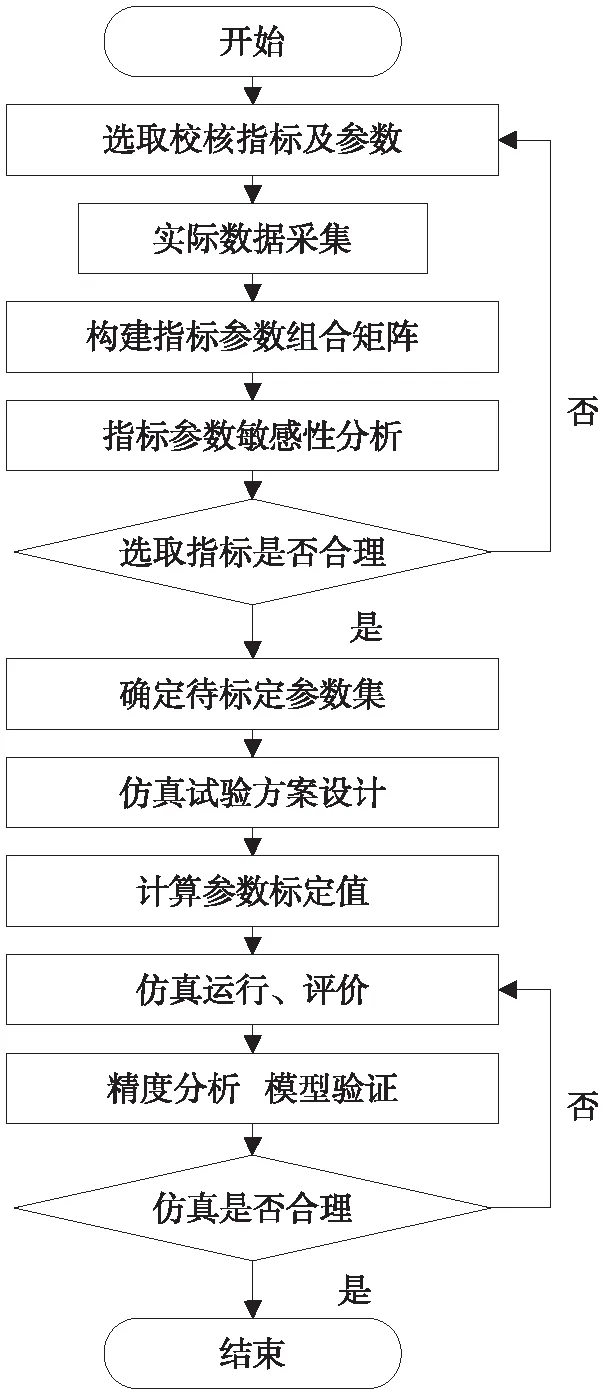
图1 模型参数标定流程
2 敏感性分析和参数标定的方法
2.1 参数选取和数据采集
2.1.1 标定参数选取
仿真模型中,国内外的车辆尺寸、道路宽度及类型等物化设施无明显差异,但驾驶习惯不同,需考虑驾驶行为的参数模型,如期望车速、跟驰模型和车道变换模型等。改扩建期间高速公路在道路线形和施工环境等方面存在较大的不同,极易引起驾驶员的心理波动。面向高速公路的跟车行为以Widemann-99模型为选取依据,变道行为使用Willmann和Sparamann的基于行为阀值的换车道模型,核心模型采用德国大学教授的生理-心理模型[11]。
因此,考虑不中断交通的改扩建高速公路特性,选取2类关键参数进行标定:一是影响交通流稳定性较大的因素j作为校核指标Ai,包括目标道路的总流量、车辆行程时间、平均延误、平均排队长度、平均速度;二是选择基于道路特征的微观参数j作为待标定参数Nj,包括跟车模型参数CCm(停车间距、车头时距、跟车变量、前后车的纵向摆动约束、进入跟车状态的阈值、消极跟车状态的阈值、积极跟车状态的阈值、车速振动、振动加速度、停车的加速度、80 km/h车速时的加速度)和换道模型参数Cn(最大减速度、可接受的减速度、消散前的等待时间、最小车头空距)。
2.1.2 实际数据采集
实际数据采集是特征路段模型建立的准备工作,在一定程度上影响交通流模拟的真实性,是参数标定中极其重要的基础性工作。通常采用随机抽样法保证样本的无偏性,样本的多少取决于研究精度需求[12]。
2.1.3 待标定参数验证
通过敏感性分析获得待标定指标和参数集,可直接采取正交试验设计法标定。将仿真输出值与实测值相对误差作为评价指标,误差值越小效果越好。考虑到交通调查的误差以及道路交通运行状态本身所具有的随机性,当拟定参数误差指标控制在5%之内时,即认为仿真值和实际调查数据有较好的拟合度,通过了有效性评价,可满足模型标定的精度要求,如式(1):
(1)
式中:Q为调查实测值;Q′为仿真运算值。
2.2 参数指标组合敏感性分析
此工作需借助搭建的交通微观仿真模型,可参考文献,选择便捷、精确的敏感性分析方法[13],对具有代表性的多个标定指标和驾驶微观参数重新组合,并确定标定指标及指标参数集。
2.2.1 参数指标组合
将众多参数组合成不同水平的指标参数集Ai·Nj,通过构建参数指标组合矩阵Pij进行敏感性分析,选出每个指标对应的标定参数相关性最大组合,如式(2):
CC1…CCnC1…Cm
P=[maxPij]
(2)
式中:Pij为参数指标组合矩阵;P为参数指标最优组合;Ai= [A1,A2,…,Ai],i= 1,2,3,4,5为校核指标集合;Nj=[CCn,Cm],j= 1,2,…,n+m为标定参数集合;CCn= [CC0,CC1,…,CCn],n= 0,1,2,…,9为跟驰模型参数集合;Cm= [C1,C2,…,Cm],m= 1,2,3,4为变道模型参集合;λi,n+m为判断指标。
2.2.2 参数敏感性分析
敏感性分析又称为参数灵敏度分析,是对仿真模型输入变量对输出变量影响程度的定量描述方法。适用于校正参数集筛选,预先有效排除标定指标重要度较低的驾驶行为参数,以减少标定工作量。构建仿真试验分析矩阵如式(3)~式(7),判定仿真参数对校核指标的敏感性。
(3)
(4)
(5)
(6)
(7)
式中:Xij为仿真试验分析矩阵;随机种子所取水平数l= 1,2,3,…,n;k= 1,2,3,…,m为仿真参数变化水平;Iij为参数变化引起试验结果标准差的算术平均值;I′ij为随机因子变化引起试验结果标准差的算术平均值;STDEVA为样本标准差函数;λi,n+m为判断指标,如果λi,n+m>1.5,判定仿真模型参数对校核指标具有影响,如1<λi,n+m<1.5,有影响,不显著,否则λi,n+m<1,无影响。
2.3 参数标定方法
全面试验法的优点在于对各因素与试验指标的关系剖析清楚,缺点是不做重复试验无法区分主次因素;简单比较法次数少但考察的因素水平仅限于局部区域。由于改扩建工程模型涉及的实际数据难以采集,亦没有数学公式科学表示,标定极为复杂,因此根据研究目的,选择相关指标与参数组合进行敏感性测试与分析。经过综合考虑决定,选择使用不同水平数之间有交互作用的多指标正交试验法,既可减少试验次数,提高效率,又可利用科学的规格化表格安排多因素试验,次数可控、精准高效,适合改扩建模型参数标定[14-15]。
3 案例应用
3.1 工程介绍与特征路段选取
选取济青高速公路改扩建工程中青岛方向K306+500路段作为参数标定工作的研究对象。既有济南—青岛高速公路为双向4车道,改扩建后采用双向8车道高速公路标准,是我国目前一次性改扩建里程最长、投资最大的高速公路改扩建工程,也是国内首次采用下面层行车的改扩建保通方案。
K306+500路段为双向2车道,经过中分带开口后变换为单车道的直行路段,中分带开口长225 m、宽3 m,车道宽度为3.75 m,如图2所示。实际数据采集时间为2018年4月,交通量为1 450 pcu/h,选取单向输入方式,入口交通流量输入2 000 pcu/h,车辆运行期望速度为80 km/h,中分带开口段限速40 km/h,小汽车与货车、大型客车的流量比为7∶2.5∶0.5,仿真时长3 600 s,有效周期时长选取其中第600 s ~ 3 000 s。
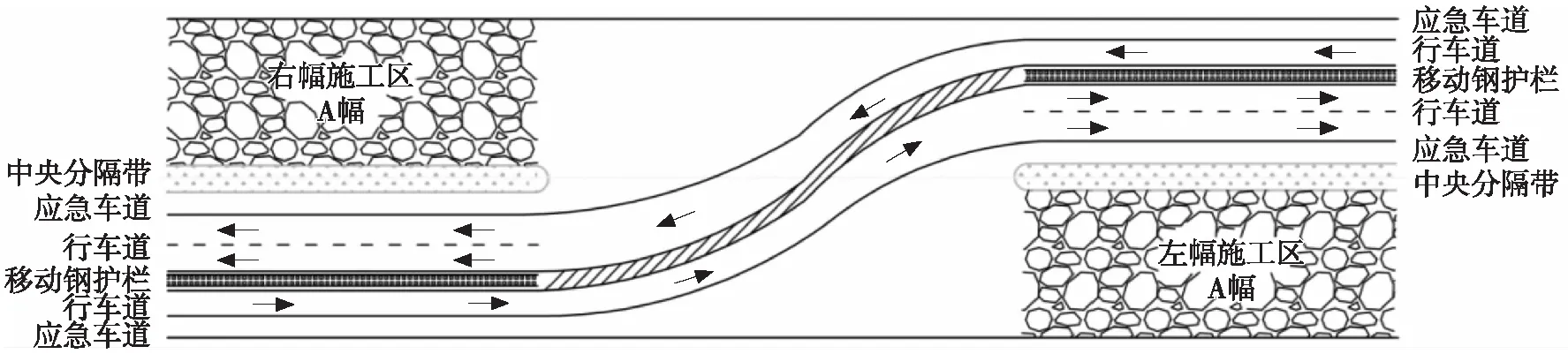
图2 K306+500段车流转换形式
3.2 试验方案设计
3.2.1 指标参数选取
仿真模型输出参数:600 s ~ 3000 s内整个路段的总流量、行程时间,中分带开口段车辆的平均延误、平均速度、中分带开口段上游车辆的平均排队长度,共5个标定指标。待标定的14个微观参数(跟驰参数CCm和换道参数Cn)默认值及取值范围参考使用手册[11]。
3.2.2 敏感性分析
采用插值法将各个参数在其取值范围内10等分,使每个仿真参数具有11个取值水平,仿真随机种子选取20、60、100、140、180共5个水平,在不同水平的随机种子下每次仿真只变化1个参数的水平值,其他参数取值设为默认值。
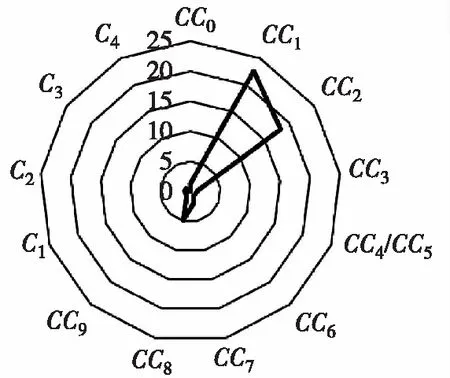
现以停车间距(CC0)为例对此路段总流量的敏感性进行分析。获取在仿真参数CC0数值变化和随机种子变化条件下的试验结果,按照式(3)~式(7)分别计算仿真输出的试验结果标准差,其最终判别指标为1.33,判定停车间距对整个路段总流量有影响但并不显著,具体结果如表1所示。
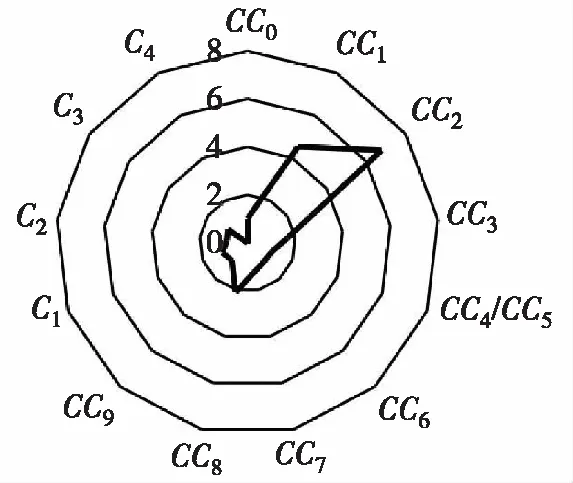
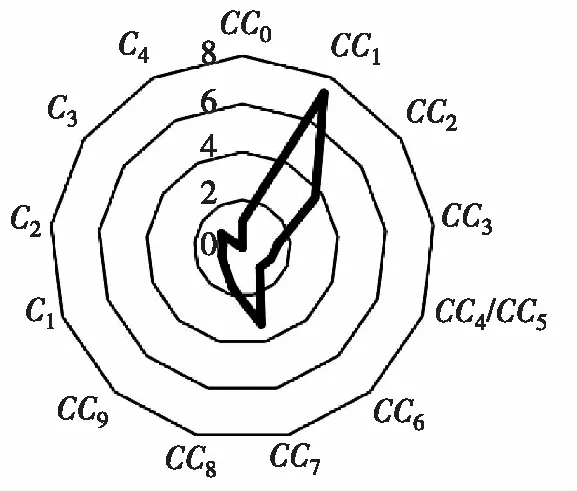
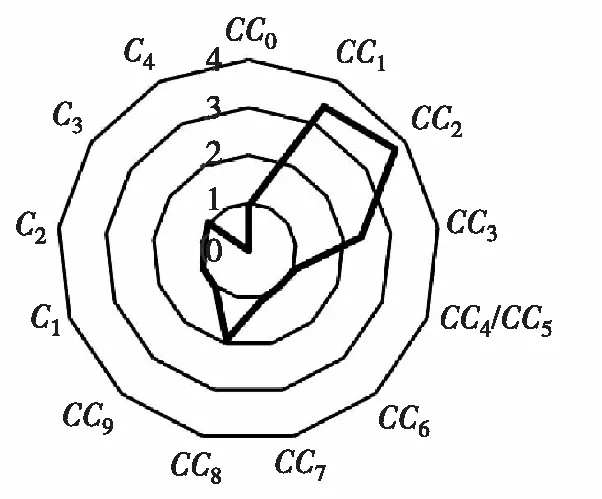
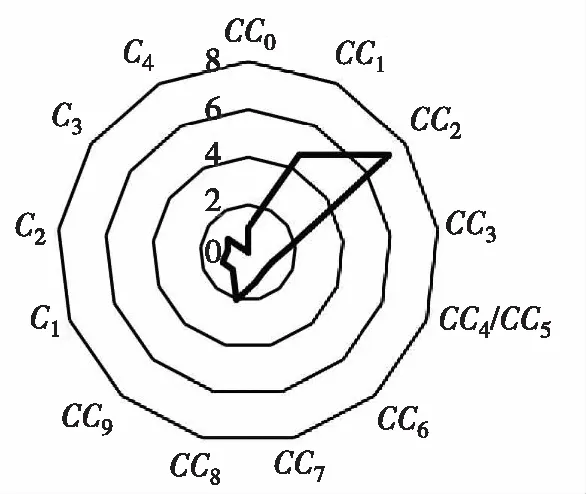
按照以上分析方法可得出其他微观标定参数对校核指标的敏感性状况,如图3所示。其中CC1、CC2、CC8三个参数对5个校核指标都有显著影响,CC7对流量和平均速度有显著影响,CC3对延误、行程时间和排队长度有显著影响。考虑到数据采集的便捷性,选取整个路段的车流量作为标定指标,CC1、CC2、CC7、CC8四个参数为标定参数。
3.2.3 正交试验法参数标定
敏感性分析的标定指标结果为路段车流量,待标定参数为车头时距(CC1)、跟车变量(CC2)、振动加速度(CC7)、停车的加速度(CC8)4个微观参数,每个参数划分3个水平。选用3水平4因素正交表L9(34)进行仿真试验,按照正交表中各参数标定试验方案的水平组合运行VISSIM仿真,9个方案分别在不同的随机种子下运行5次,对试验结果进行极差分析,得出不同因素不同水平值对试验指标的影响程度及主次顺序,进而确定最优因素水平组合:CC1=1,CC2=5,CC7=0.6,CC8=7。
3.3 标定参数精度分析
敏感性分析选取5个标定指标和14个微观参数,选取受参数影响较多的指标作为微观交通仿真的参数标定指标。正交试验将路段车流量指标与待标定的4个微观参数重新科学组合成参数集最优解,再次仿真输出的流量为1 428,标定后的最优仿流量值与实测数据接近,误差在可接受范围内。
对4个微观参数标定结果的均值进行主效应验证,每个参数划分为3个水平,如图4所示。由图4可知,趋势线不平行于横轴表示存在主效应,线越陡峭主效应量值越大,故经验证所用标定组合有效。
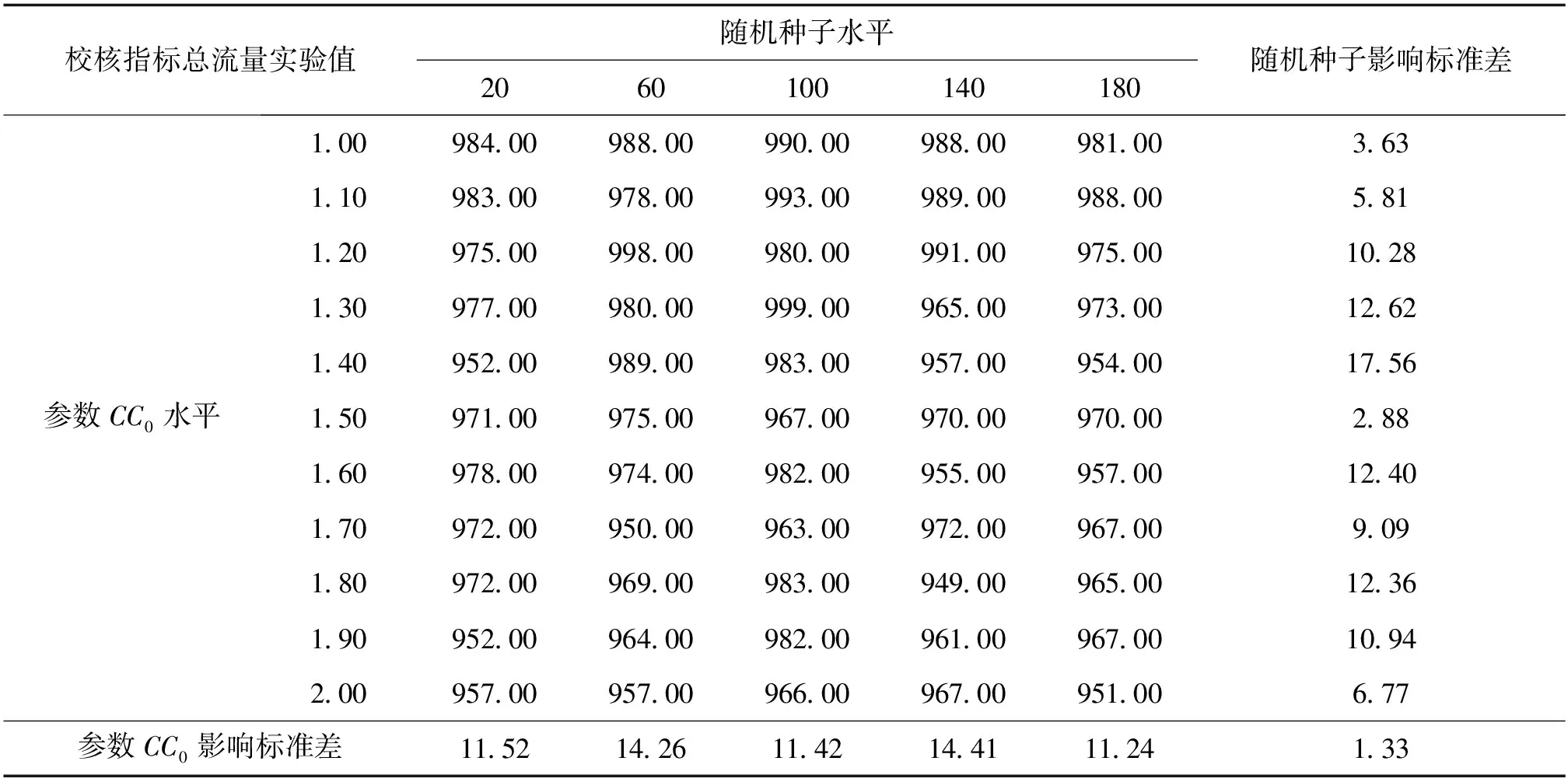
表1 停车间距(CC0)对总流量敏感性分析
(a) 延误对参数敏感性
(b) 流量对参数敏感性
(c) 速度对参数敏感性
(d) 排队长度对参数敏感性
(e) 行程时间对参数敏感性
最终微观参数标定结果如表2、表3所示,其他参数保持缺省值不变。
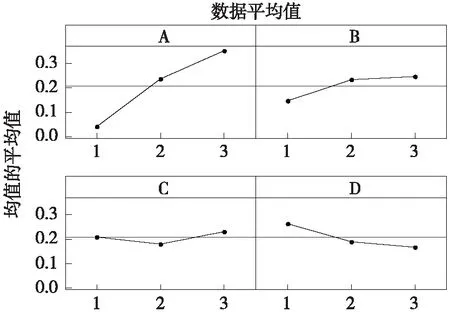
图4 标定结果均值的主效应验证
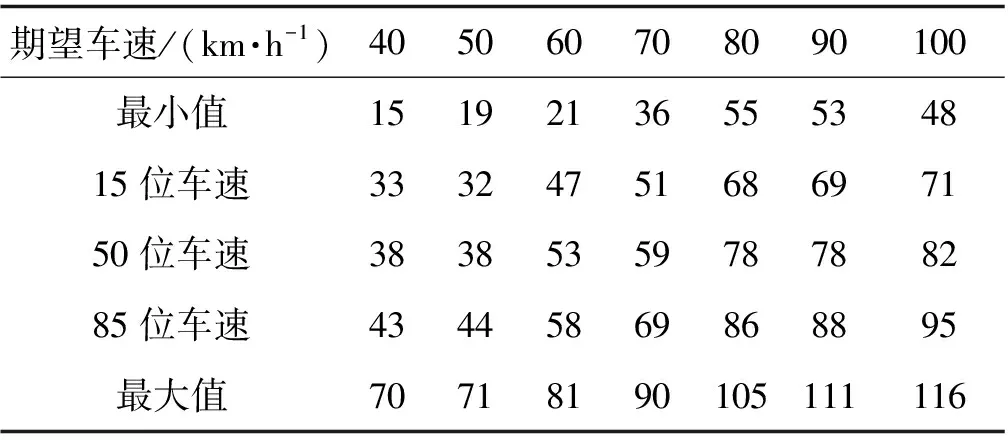
表2 期望车速标定参数结果

表3 驾驶行为标定参数结果
4 参数标定结果对比分析
为了验证本文提出的敏感性分析与正交试验相结合的参数校正方法具有科学性、实用性和有效性,搜集国内外部分高速公路的参数标定结果进行对比分析,结果如表4所示。
A列采集美国880号州际公路自南向北方向(简称1-880N)交织区内1 d的实际数据,目的是建立实时事故风险预测模型[16]。将每30 s车辆速度仿真结果值与速度分布默认值、计算事故风险值与事故风险分布默认值比较,发现此模型CC4~CC7校正值与缺省值差别较大。B列以广深高速公路广州收费站建模[17],标定值变化幅度较大,表明该模型可作为大流量高速公路普通路段的参考依据。C列以新建邢衡高速为仿真对象[18],考虑了匝道入口处的交通流特性,针对部分跟驰参数进行校正。
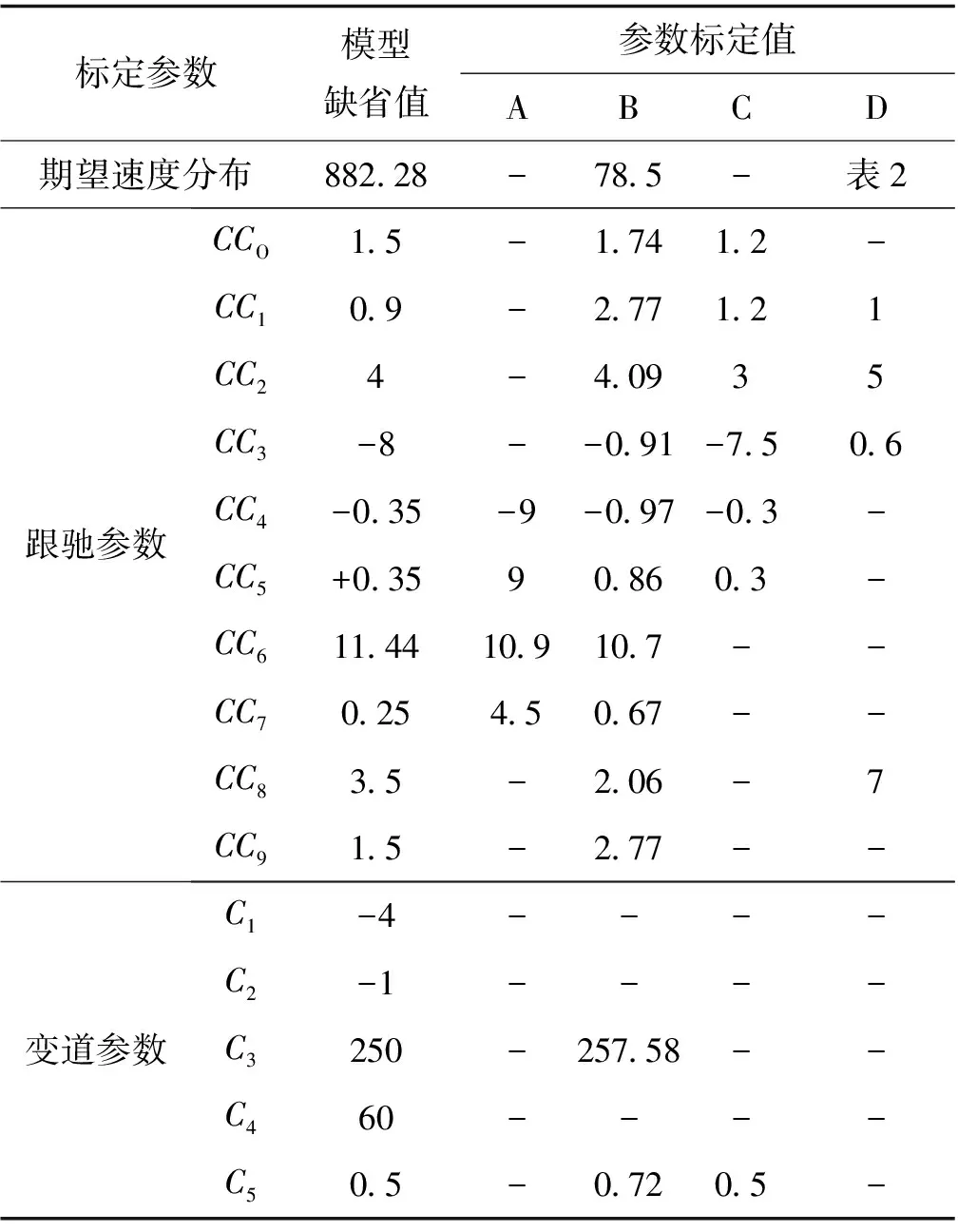
表4 不同高速公路的参数标定结果对比
D列是本文案例标定的参数值。通过对比分析可知,不同的场景参数有明显差异,需要特殊问题特殊研究。本文提出的方法以实际地点车辆速度的调查数据对期望车速进行详细标定,并选择14个跟驰模型和变道模型的参数进行标定,全面具体,贴近实际,标定好的模型可同时对不间断交通的高速公路改扩建期间大量问题路段的仿真进行研究。此外,经由完善的标定方法借助科学有效的方式筛选出影响程度较高的参数水平组合,在一定程度上可以减少数据采集和标定工作量。
5 结束语
针对不中断交通的改扩建工程特点,完善了仿真参数标定流程,提出了敏感性分析与正交试验相结合的参数校正方法,并校正关键参数指标涉及的驾驶行为参数模型。
以济青高速改扩建工程为例,通过敏感性分析筛选出5个基于道路特征的微观参数j作为校核指标Ai,基于参数j选取14个跟驰模型参数CCm和换道模型参数Cn,作为待标定参数Nj,由此克服了指标选取的盲从性,降低了标定复杂度和工作量。通过正交表格设计科学有效的仿真方案,找出具备均匀分散、齐整可比的最优水平组合作为参数标定结果。经案例应用分析并评价仿真运行结果发现,CC1=1、CC2=5、CC7=0.6、CC8=7为最优因素水平组合。研究结果为今后类似的改扩建高速公路仿真模型构建提供了借鉴。
