公路边坡数值模型几何尺寸的影响分析

潘永坚， 王华俊， 卿翠贵， 张 建

(1.浙江省工程勘察设计院集团有限公司， 浙江 宁波 315012； 2.宁波大学 土木与环境工程学院， 浙江 宁波 315211)

在公路边坡设计过程中通常涉及到大量的数值计算，以确定最优坡比及相应的支护方案，数值计算结果是工程决策的重要依据[1-2]。为了提高计算效率，数值计算过程要在计算效率与计算准确性之间达到平衡。由于数值模型存在边界约束条件，构建合理的数模是获得可靠参考数据的前提[3]。闫东晗等[4]对一边坡模型(取右侧边界R= 2.5H、下侧边界B= 2H、左侧边界L= 1.5H，H为坡高，各参数的意义见图1)利用强度折减法计算时，发现采用二维模型左侧边界对计算结果影响次于下边界。郭昊天等[5]在对路堑高边坡进行分析时，采用了类似R=H、B=H、L=H的等边界尺寸模型进行计算，并对相关工程案例进行了分析。任晋岚等[6]在进行强度折减计算时，为了减小尺寸效应的影响，建模时将模型的边界尺寸尽可能扩大，以减小边界约束条件对计算结果的影响。孙志杰等[7]在物理模型试验中，采用坡体宽度大于高度的物理模型试验，以降低模型尺寸边界对物理试验结果的影响。Ma等[8]在三维数值分析中比较了运算时间长度，当W=H时(W为三维模型宽度)，所得三维模型进行分析结论较为可靠。张坤勇等[9]采用W> 6H的模型进行计算时，发现可以将三维问题简化为二维问题来处理，以减小运算时间，但当W< 3H时，数模的三维效应应当被考虑。陈达章等[10]认为W取值较小时，会对计算结果有较大影响，取坡体模型宽度为坡高的一倍以上时可满足精度要求。

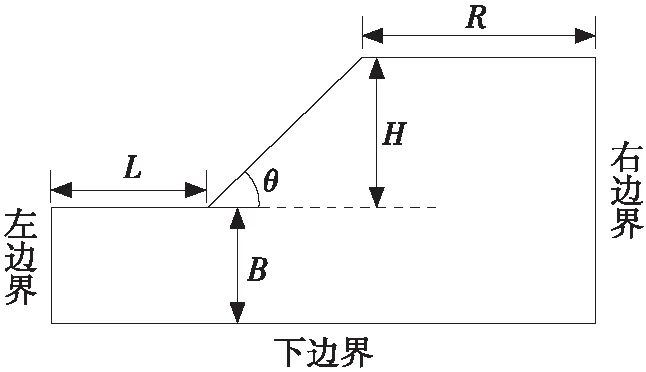
图1 边坡数值模型几何参数示意

在工程应用过程中，盛晓杰等[11]通过延长模型边界的方法进行计算，但是并没有考虑到模型尺寸与计算结果可靠性的关联。谢洪斌等[12]在研究高边坡在动力作用下的动力响应特征时所采用的模型边界取值偏小，其对结果的影响也缺乏进一步说明。王钰[13]在对经典模型进行计算时，分析了3种典型模型，但所采用的尺寸各不相同，模型尺寸对分析结果的影响并未详细说明。

基于以上文献分析，目前对坡体数模尺寸的选用并没有统一的分析结论。在构建数值模型过程中，通常不考虑计算效率，取较大的边界值以获得准确的计算结果。为了获得较准确的分析结果及较高的计算效率，数值模型尺寸到底该如何设计，是值得进一步讨论的问题。鉴于此，本文采用系统分析的方法，分别讨论基于强度折减法[14]及有限差分软件(FLAC3D)[15]在进行二维及三维边坡模型分析时，数模尺寸对分析结果的影响，阐述数值模型对几何尺寸的敏感性，并给出针对模型构建的实用性建议。

1 二维模型边界尺寸影响分析

初始分析模型先在有限元软件ANSYS中构建，划分网格后将模型的节点及单元尺寸信息导入FLAC3D中构建最终的分析模型。所有模型均采用相同的网格密度，划分的最小网格单元体尺寸为2 m。数模的上部为自由界面，无任何约束，下边界为全约束，左右界面采用法向约束，即不可水平方向发生位移。取坡高H= 20 m，左侧边界L= (0.25-3.5)H，右侧边界R= (0.25-3.5)H，底部边界B= (0.25-3.5)H。土体的强度计算本构关系采用经典的摩尔-库伦准则。计算过程中涉及到的土的物理参数为：土体重度γ= 20 kN/m3，内聚力c= 20 kPa，内摩擦角φ= 20°，弹性模量E= 30 MPa，泊松比v= 0.3。

1.1 模型几何尺寸与坡体安全系数的关联分析

1) 3处边界取值相同的情况

设计如下试验：取L=R=B=C，C有0.25H、0.5H、H、1.5H、2H、2.5H、3H、3.5H等共计8组取值，坡角θ=45°。通过等比例逐步扩大模型的边界尺寸，计算得到的安全系数FS见表1。

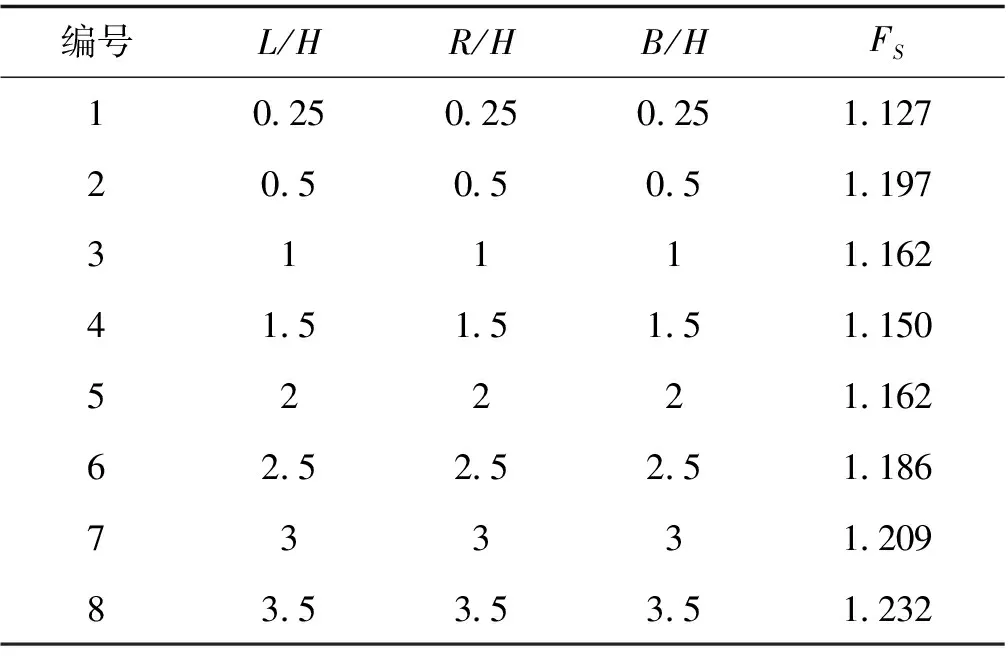
表1 等边界条件下的安全系数求解结果

从表1可以看出，计算所得的坡体安全系数随边界取值的不同呈波动变化。在该组试验中，最大安全系数与最小安全系数的幅度相差7.2%，从第3组取值开始，模型尺寸越大，计算所得安全系数逐渐递增，计算所需要的存储空间及计算时长也逐步增加。

根据以上分析，当模型的边界约束尺寸较坡体本身的尺寸较大时，计算所得的安全系数相对较大。但这个较大的安全系数并不是对工程实际的真实反映，因为求解模型来源于简化的工程实体，以牺牲运算效率为代价，为增加数值分析结果与实际问题解的接近程度的做法，并没有具体的实际意义。因此，在合理的取值范围内，解算结果偏于安全的边界取值才是数值分析搜寻的目标。针对表1的计算结果，数值模型中3处边界取值均为1.5H时，所得的安全系数相对较小，用此时的安全系数评价边坡的稳定性结果偏于安全，可用于实际参考。

为了进一步分析坡角大小对计算结果的影响，分别取坡角为30°、39°、45°、51°、60°进行试验，边界取值从0.5H递增至2.5H，等间隔设置递增幅度，结果见图2。由图2可知，坡角会对计算结果产生影响，随着模型边界尺寸的增加，坡角分别为为30°、39°、45°、51°、60°时，安全系数的波动幅度分别为1.5%、2.8%、4.1%、2.2%、1.6%。其中，坡角取值θ=45°时，安全系数的波动幅度最大，可作为分析边界尺寸时的一个典型的坡角取值情况。

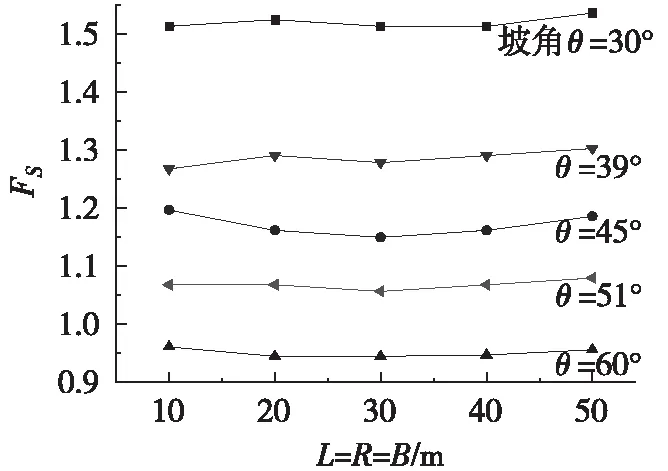
图2 坡角及边界大小对分析结果的影响

2) 3处边界取值不相同的情况

以上分析是建立在坡体左侧边界、右侧边界、上边界取值相同的假设情况下进行的。为深入分析3处边界取值不等的情况下坡体数模尺寸对分析结果的影响，试验根据前述分析，取典型情况(坡角θ=45°)进行分析。具体方案为：将数模的右侧边界和下边界固定取值为1.5H，左侧边界则由0.5H递增到3.5H，找到最佳的左侧边界取值；再在此基础之上，固定左侧边界和下边界，变化右侧边界，找到最佳的右侧边界取值；最后变化下边界，确定最优的模型边界取值。试验设计方案以结果继承的方式进行，主要目的是为了有效控制试验次数，使问题简化可解。

得到的分析结果见表2。分析可得，左侧边界的变化对分析结果有一定影响，随着左侧边界尺寸的增加，计算所得结果略有波动，最大变化率为1.4%。其中，考虑到第1组试验因左侧边界取值太小，认为边界约束条件对计算结果产生较大影响。左侧边界取值H和1.5H时所得的安全系数较小，左侧边界取值为H时，所得安全最小为1.148。当左侧边界取值不小于2H时，计算所得坡体安全系数近似趋于稳定。考虑到使安全系数计算收敛的边界值因坡角等取值的变化而变化，根据前文对数值分析结果取用原则的界定，确定左侧边界的最优取值为H，即可保证计算结果的可靠性及运算效率。

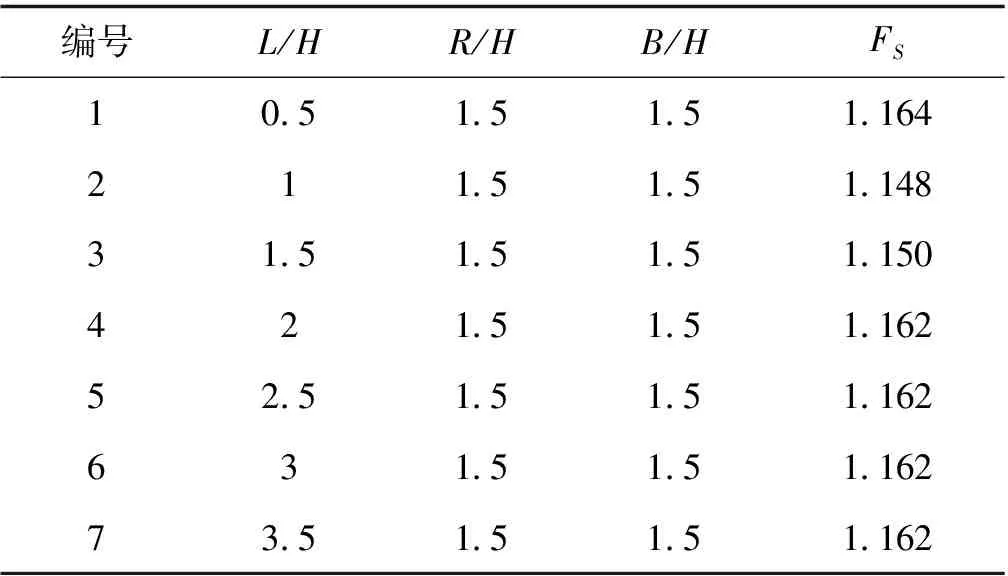
表2 左侧边界对分析结果的影响

根据表2的分析，设计下一步试验：将模型的右侧边界尺寸由0.5H逐步递增到3.5H(增幅固定)，左侧边界与下边界分别固定为H和1.5H，所得计算结果见表3。根据表3的结果，认为第1组取值不可靠，不予考虑。在左侧边界取值H、下边界取值1.5H的情况下，右侧边界取值为H及1.5H时所得的安全系数最小，均为1.148。

为进一步确定下边界的最佳取值，取左侧边界为H，右侧边界分别取值H(A组试验)与1.5H(B组试验)，下边界取值由0.5H递增至3.5H，递增幅度为0.5H，所得安全系数见表4。由表4可知，在右侧边界分别取值H与1.5H时，随着下边界的变化，安全系数均有一定波动，右侧边界取值H、1.5H时，波动幅度分别为2.8%、4.1%。当左侧边界取值为H、下边界取值为1.5H，右侧边界取值H和1.5H时，所得安全系数均为1.148。由此可知下边界的最优取值为1.5H。

表3 右侧边界大小对计算结果的影响

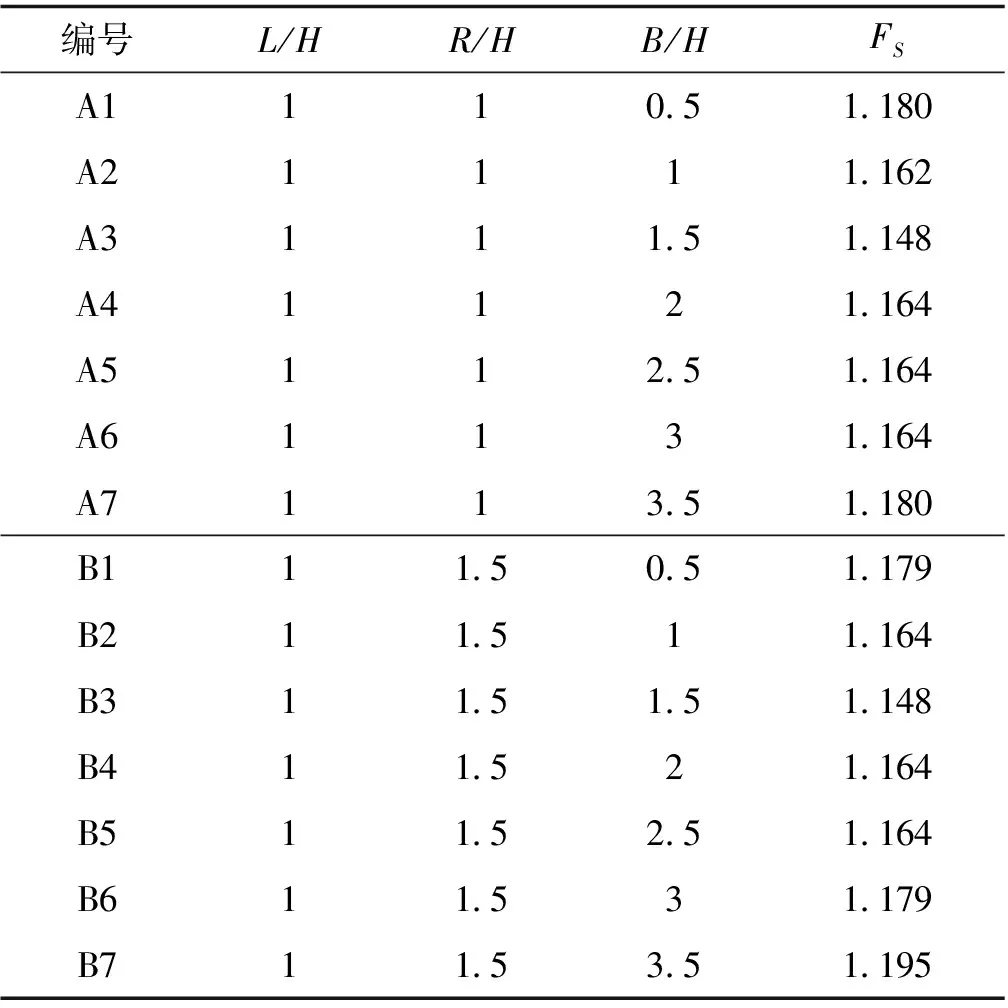
表4 坡体底部边界大小对计算结果的影响

在左侧边界取值H、底边界取值1.5H时，右侧边界分别取值H和1.5H的模型运算平衡状态下的剪应变增量云图见图3。从图3可知，右侧边界取值H时的剪应变增量比取值1.5H时的剪应变增量小，且后者的剪应变区域要比前者的大，但两者的剪应变区均已由坡脚贯穿至坡顶，2种情况在这一点上差异很小。考虑到边界越大，解算时间越长，建议右侧边界取值为H。

1.2 二维模型尺寸选用建议

等边界取值建模时(即模型的左侧边界、右侧边界与底边界的尺寸取值相同)，取3处边界值均不小于1.5H时，结果较为可靠。在等边界试验所得结果的基础上，以结果继承的方式设计试验，获得分析模型左侧边界的最佳取值为H，右侧边界取值为H，底边界取值为1.5H。此时，数值分析所得安全系数取值可靠且运算速率快。

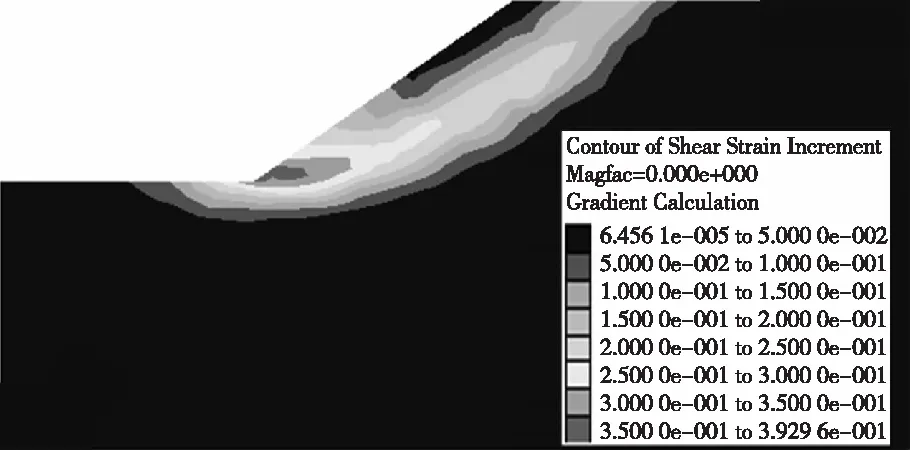
(a) L=H，R=H，B=1.5H

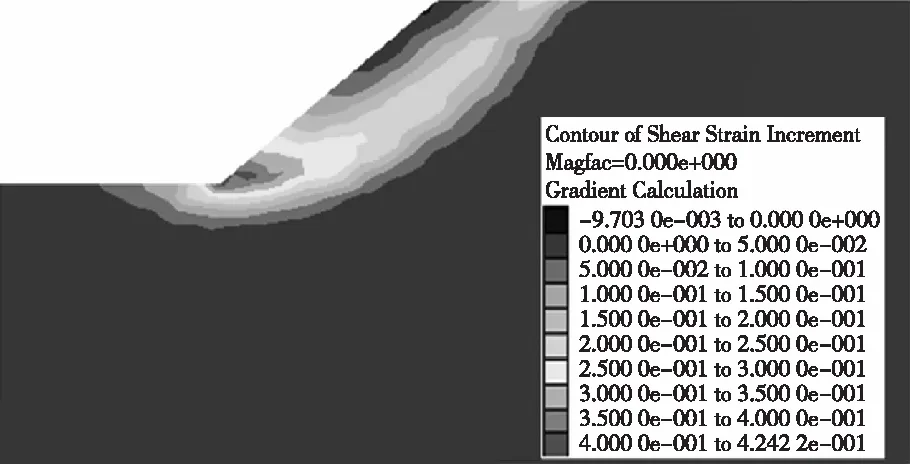
(b) L=H，R=1.5H，B=1.5H

2 数值模型三维效应分析

为得到三维数模计算精度与运算速度之间的平衡点，在二维数模分析结论的基础上开展三维模型尺寸效应的分析研究。相比较于二维数模分析情形，模型三维效应的区别主要体现在模型宽度对数值分析结果的影响上。设计如下试验：模型左侧边界取值H(本次分析过程中H=20 m)，右侧边界取值H，下边界取值1.5H，模型宽度从1 m(0.05H)逐渐增加至70 m(3.5H)，作为对照，坡角分别为27°、45°、63°三种情形进行试验，模型下边界完全约束(无自由度)，左右侧边界法向约束(只能在上下方向上发生位移)，与y轴垂直的边界也采用法向约束，模型上部为自由边界。计算过程中采用的土体参数均与二维试验的土体参数相同。数模试验分析结果见表5。

从表5的计算统计数据可得出，三维数模的宽度对计算结果有一定影响，在不同坡角情况下，随着模型宽度的增加，安全系数均逐渐增加并最终趋于稳定。对于边坡宽高比为2∶1(坡角为27°)的情形，当模型宽度取值大于等于H(20 m)时，坡体安全系数取值趋于稳定为1.709，相较该坡比情形下的二维模型(宽度为0.05H)，计算结果的偏大约4.8%。对于边坡宽高比为1∶1(坡角为45°)的情形，当模型宽度取值大于等于1.25H(25 m)时，计算所得安全系数趋于稳定为1.258，与该坡比下的二维模型计算结果相比较，计算结果的偏大幅度达到了9.6%。对于边坡宽高比为1∶2(坡角为63°)的情形，三维模型计算结果与二维模型结算结果的最大偏差达到了8.5%。因此，三维模型的构建宽度及坡比均对分析结果有一定影响。

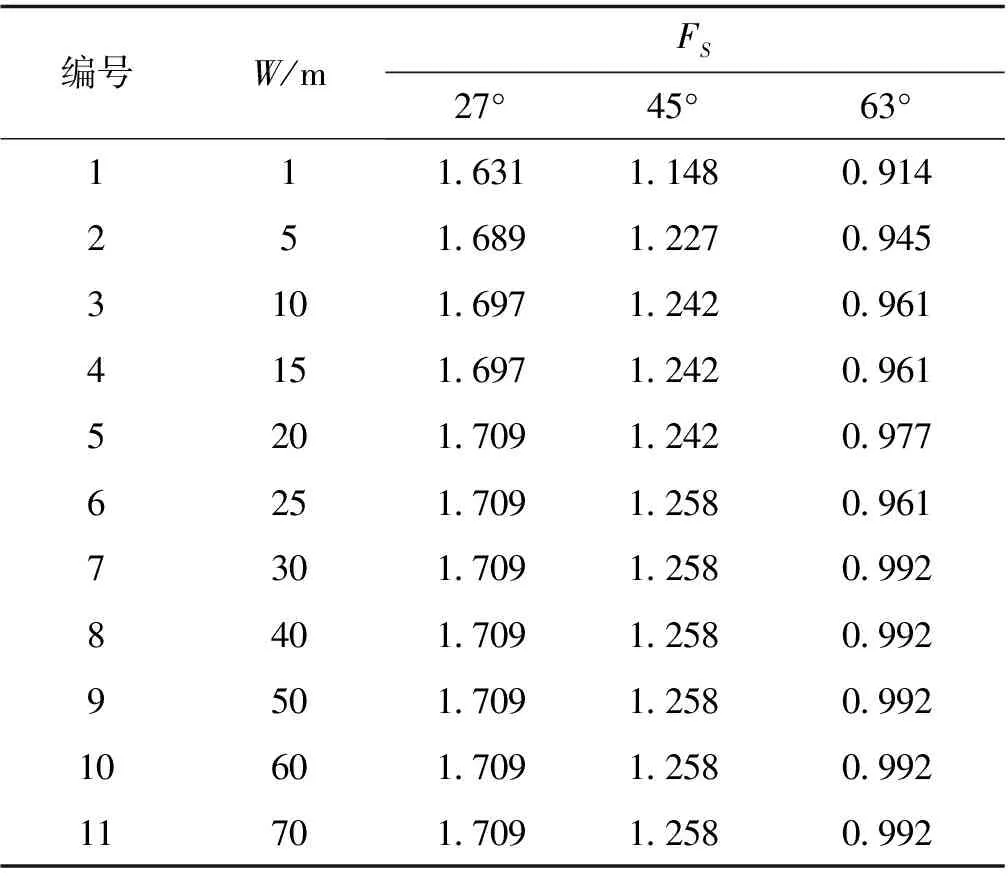
表5 模型宽度变化对安全系数的影响

3 结论

1) 二维数值模型边界尺寸对分析结果的影响受坡角的影响，坡角小于30°和大于60°时，边界效应对分析结果的影响不明显，坡角取值45°时，分析结果对边界效应最敏感。二维模型的左侧边界、右侧边界及底边界的取值均小于坡高H时，边界约束效应对计算结果的影响较大，计算结果的准确性较差。当左侧边界与右侧边界均不小于H、底边界不小于1.5H时，计算结果较为可靠。

2) 三维模型解算结果普遍大于二维模型解算结果，随着三维模型宽度的逐渐增加，计算所得安全系数呈递增收敛趋势，收敛速度受坡角的影响，坡角越小收敛越快。若左侧边界、右侧边界、底边界分别取值H、H、1.5H，对于坡角小于45°的情形，模型的宽度取值应不小于H；对于坡角大于45°的情形，模型的宽度取值应不小于1.5H。