基于 Floyd 算法的制造/再制造闭环物流网络优化

段丽梅,唐克生,李依蓉,王艺丹

(昆明冶金高等专科学校商学院，云南 昆明 650033)

0 引 言

我国的《物流术语》中将逆向物流定义为“不合格物品的返回、维修以及周转使用的包装容器，从需求方返回到供应方所形成的回收物流和将经济活动中失去原有使用价值的物品，根据实际需要进行收集、分类、加工、包装、搬运和储存，并分送到专门处理场所时所形成的废弃物物流”。逆向物流根据不同的处理方式、不同的回流节点可以分为再制造、再利用、再循环和废弃处理等方式[1]，如图1所示。

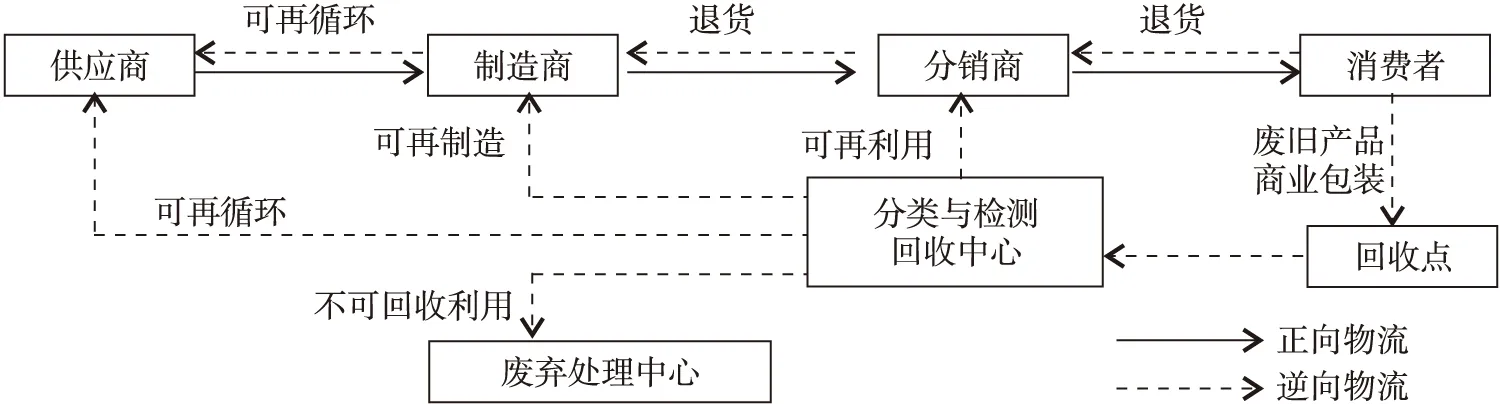
图1 逆向物流不同的处理方式Fig.1 Different treatment methods of reverse logistics

本文仅讨论逆向物流中的再制造类型。再制造网络通常针对具有较高回收价值的电子产品，汽车，电器等部件。再制造物流包含将废旧产品从消费地运回生产地的逆向物流，以及将再制造产品从生产地运往消费地的正向物流，涉及废旧产品收集、检测/分类、再制造和再分销等诸多环节，是一种闭环物流。

在逆向物流所涉及的各种处理方式中，再制造逆向物流网络研究是热点，很多学者针对再制造逆向物流网络设计进行了研究。Lee等[2]给出了一个再制造系统三层物流网络设计模型，目标确定为逆向物流中的运输成本和固定成本之和最小，为求解模型，提出了一个改进的基于权重进行编码和运用新的交叉算子的遗传算法。Zarei等[3]研究生产商延伸责任制下的报废车辆再制造逆向物流网络设计，将新车的配送和报废汽车的回收结合起来考虑，假设新汽车的配送商也负责报废汽车的回收，建立了建设成本以及相关的运输成本最小化网络设计模型，最后设计了遗传算法对模型求解。Alumur等[4]研究可再制造产品的逆向物流网络设计，包括报废的电脑、洗衣机、烘干机等，指出企业如果只关注于生产商延伸责任，则将逆向物流外包给第三方。王圣池等[5]研究了跨国企业再制造逆向物流网络布局，并考虑了物流网络运营收益和物流绩效指标双目标。马祖军等[6]对再制造逆向物流与正向物流网络的集成优化设计进行了研究，建立了混合整数非线性规划模型，其重点在于集成制造系统与再制造系统的正向-逆向物流网络。

制造/再制造物流网络的优化设计，就是根据流通总成本最小化的原则，来确定每一件产品和废旧回收品的流通渠道。本文提出了一种基于Floyd算法的物流网络优化选择模型，在考虑正向物流设施能力限制的条件下，选择一条总成本最小的流通路径，使得整个物流网络的流通总成本最小。物流设施的运营能力限制通常会出现在正向物流网络中，逆向物流由于物流量通常较小，故不需要考虑设施的能力限制。

1 模型描述

本文改进的Floyd算法模型仅计算两设施之间的最小总成本，未考虑设施能力限制因素。为了模型计算的简便和准确，特作如下假设。

1.1 模型假设

1)仅考虑回收再制造一种废旧产品，且通过回收中心进行回收，正/逆向物流共用设施，即同一生产企业可以生产新产品和循环产品，新产品分销中心同时也是废旧产品回收中心，新产品的末端配送中心可以是废旧产品回收点。

2)各设施运营成本、设施间的运输成本等是确定的和已知的。

3)不同的生产企业都可以对回收产品再制造，即存在A产地生产的产品回收至B产地再制造的情况。

4)不考虑原材料供应环节。

1.2 算法说明

我们将整个制造/再制造系统以图的方式来简化表达，节点代表设施，节点间的连线代表物流运输，连线上的数值代表两设施节点间的单件运输成本。

我们采用改进的Floyd算法[7-8]来计算制造/再制造闭环物流网络中所有设施顶点对之间的最小运营和运输成本。Floyd算法是一种基于迭代思想的动态规划算法，本文增加了设施的运营成本(比如企业的生产成本和分销中心的周转成本)，算法也相应地作出了改进。算法的主要部分如下：

声明并初始化成本代价矩阵C(0)[i][j]，正向物流设施运营成本数组F[k]，逆向物流设施运营成本数组R[k]。

for(i=1;i=G.vnum();i++)

for(j=1;j=G.vnum();j++)

if(i==j){C[i][j].cost=0;}

if(i>j){C[i][j].cost=R[i]+C[i][j]+R[j];}

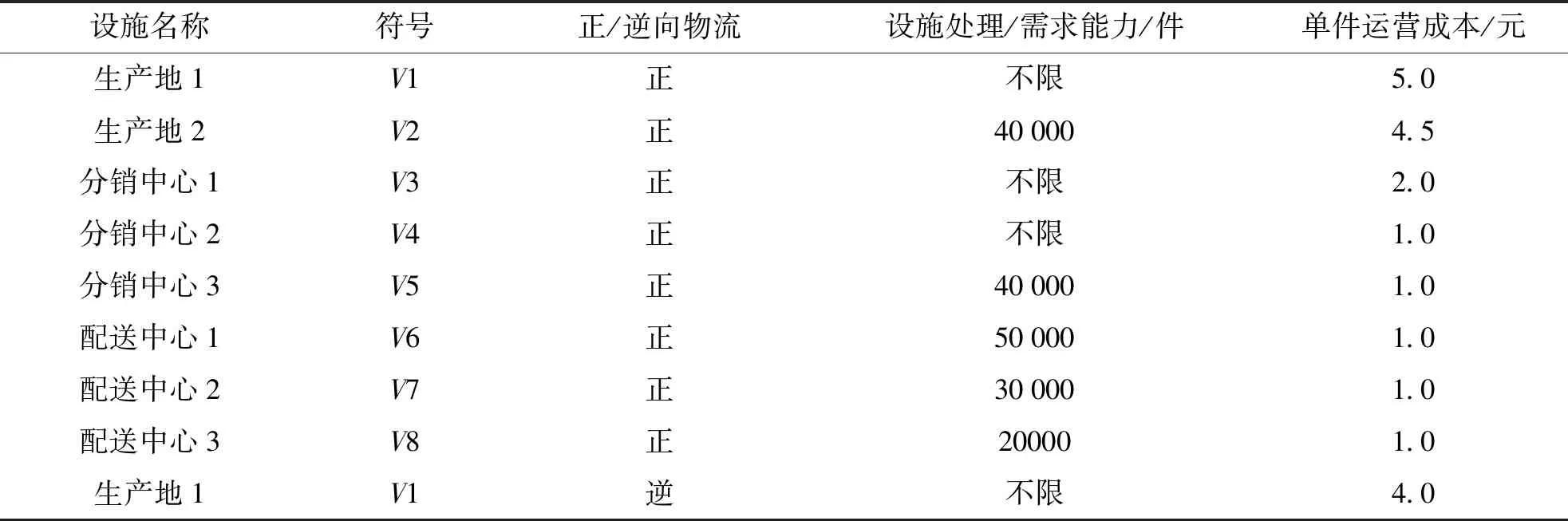
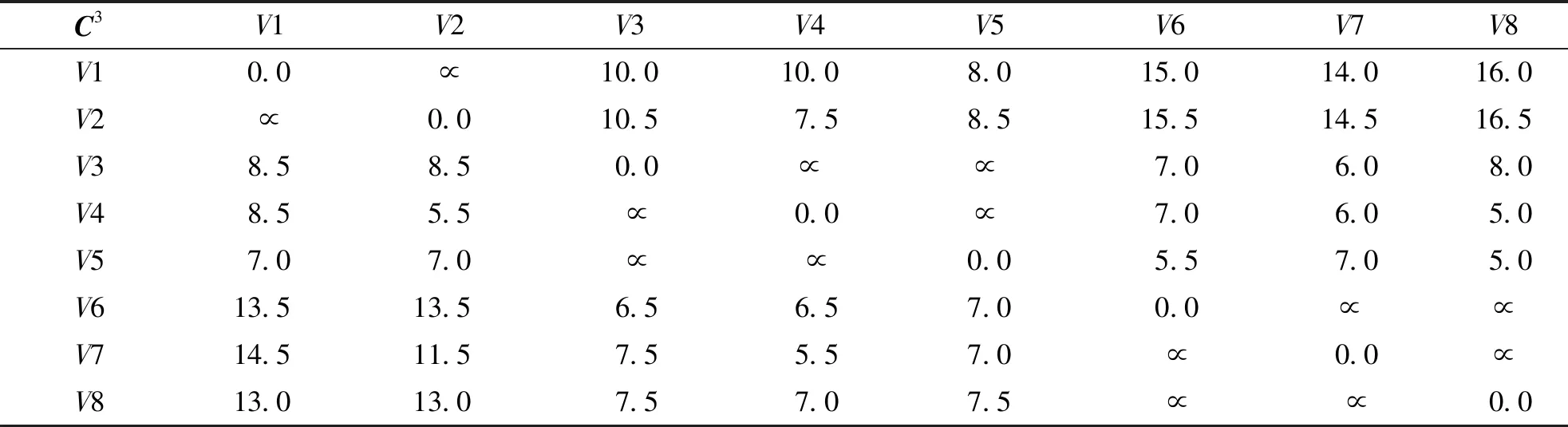
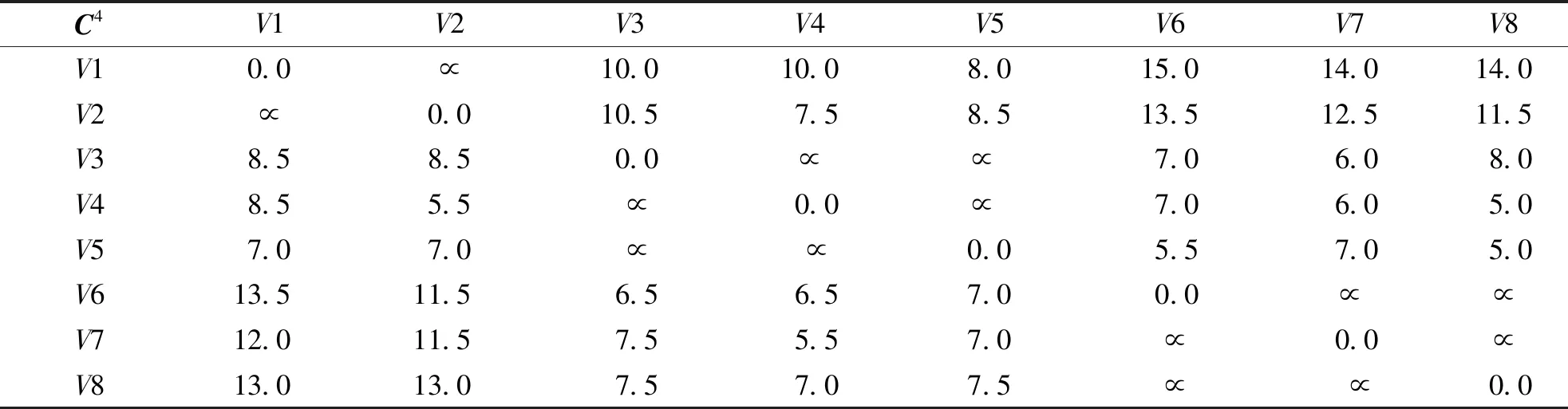
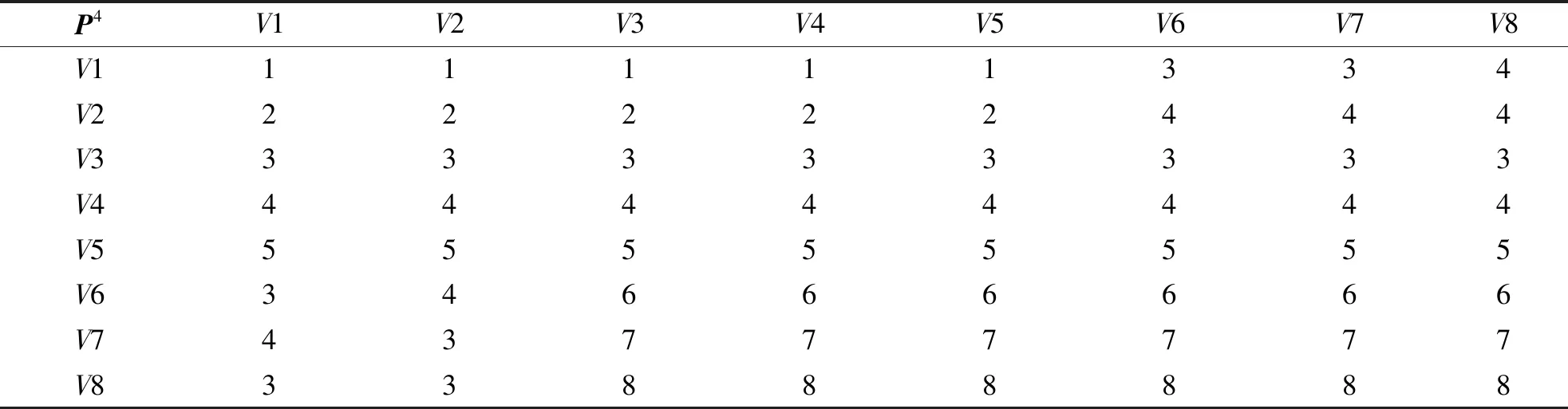
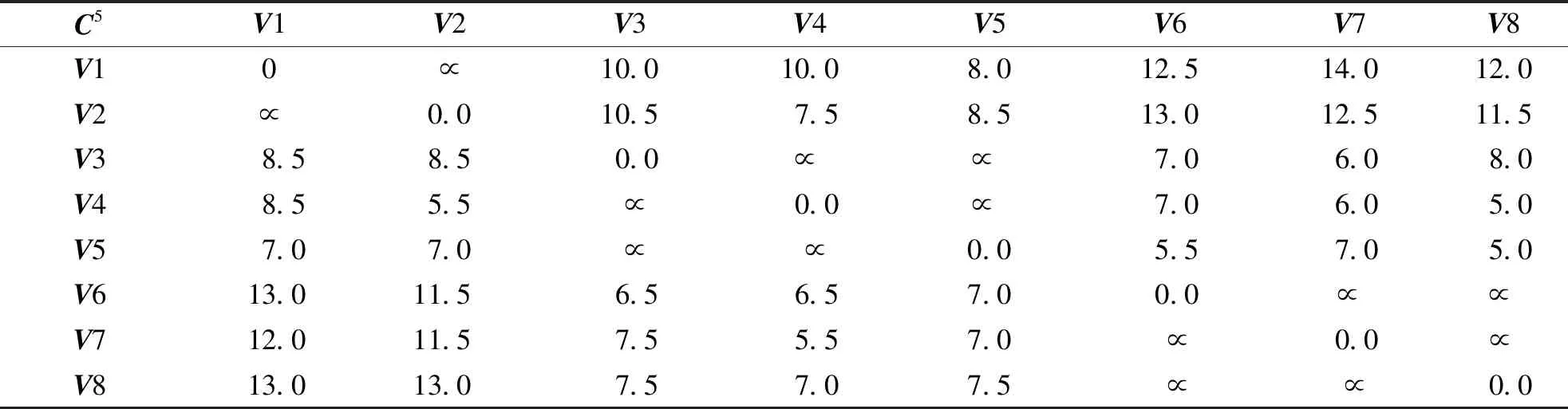
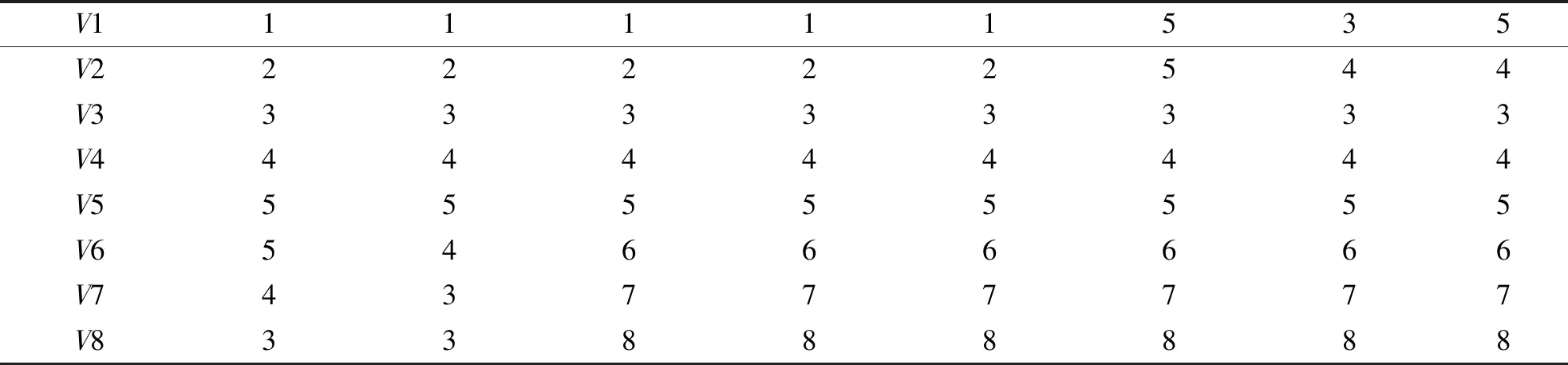
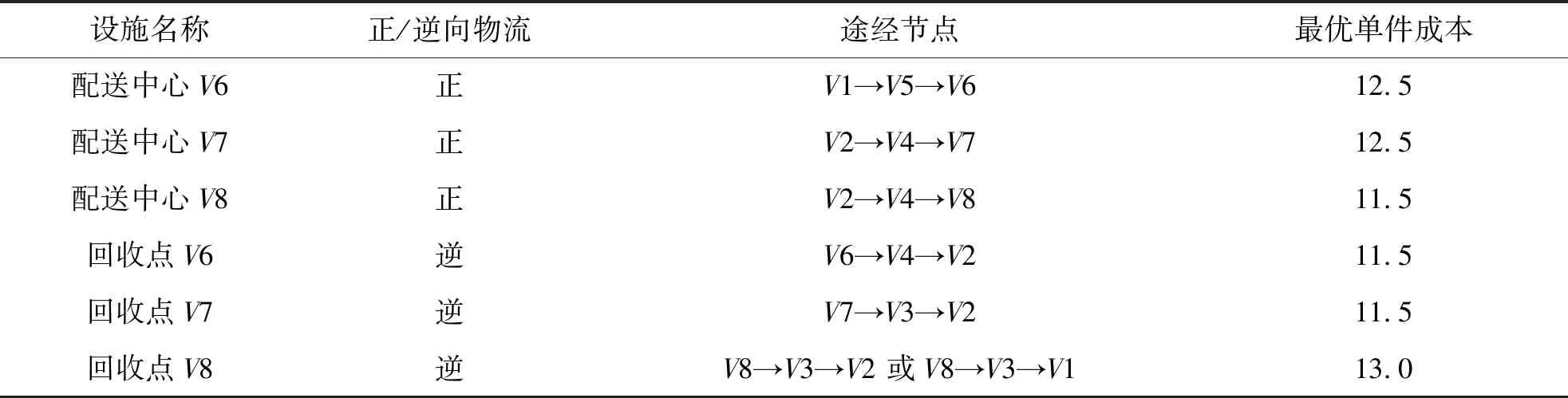
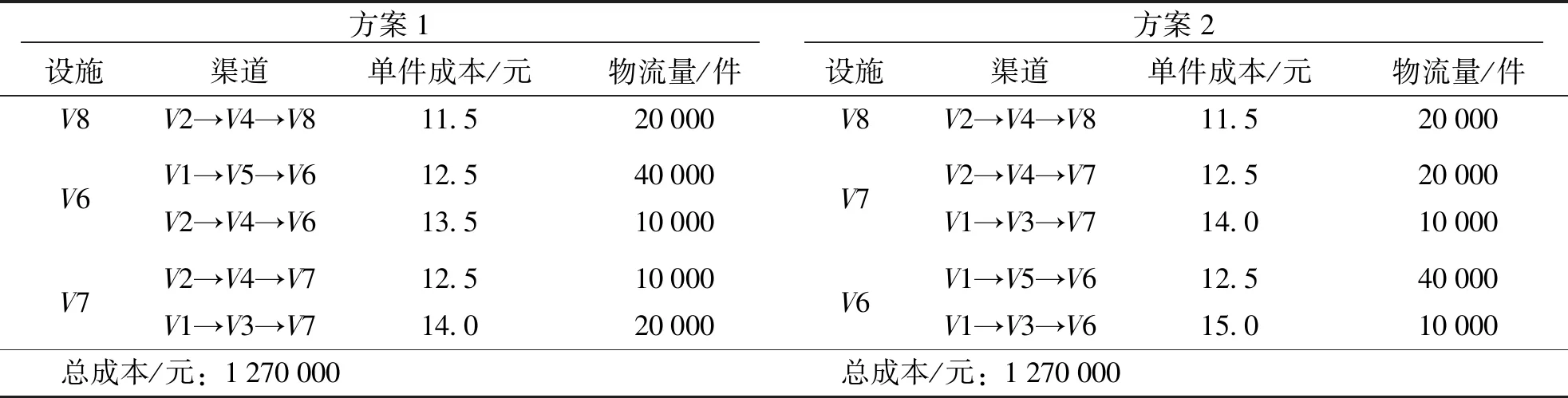
C[i][j].cost=F[i]+C[i][j]+F[j];//C(0)[i][j]直达两节点间赋初值for(k=0;k

for(i=0;i

for(j=i;jC[i][k].cost +C[k][j].cost+F[k])

{C[i][j].cost=C[i][k].cost+C[k][j].cost+F[k];

C[i][j].pre=k;}//正向物流部分

for(j=i;j==0;j--)

if(C[i][j].cost>C[i][k].cost +C[k][j].cost+R[k])

{C[i][j].cost=C[i][k].cost+C[k][j].cost+R[k];

C[i][j].pre=k;}//逆向物流部分其中，G.vnum()为节点数函数，C[i][j].cost为节点Vi与节点Vj之间的运输成本代价，C[i][j].pre为存储节点Vi与节点Vj之间的前驱节点(跳节点)。根据模型运行结果，可以得出所有节点对(两设施)之间的最小总成本，计算一次循环(产品/废旧品的正向/逆向物流完成)所经过的各个设施的各种可能路径的总成本，通过比较得出其中一条总成本最小路径，算出最小成本，并给出本次循环的途经设施节点顺序。

2 算法仿真

某产品制造商已经建设有一个制造/再制造集成物流网络，现需要对现有网络的流通渠道进行优化设计。已知有2处生产地，3个分销物流中心/回收中心(正/逆向物流共用)，3个消费地配送中心/回收点(正/逆向物流共用)，它们的设施处理/需求能力、运营成本和符号表示如表1所示。在正向物流过程中，我们对部分设施的能力上限作了设定，逆向物流由于通常物流量均较小，在此不予考虑。

表1 集成物流网络的设施运营成本、处理/需求能力Tab.1 Facility operating cost,processing/demand capacity of integrated logistics network

续表Continued

集成物流网络示意如图2所示，节点间的连线表示运输，单件运输成本用数字标注在连线上，无符号线段表示双向运输的成本相同，有向线段表示双向运输的成本不同，其中括号外数字表示正向物流的单件成本，括号内数字表示逆向物流的单件成本。

图2 集成物流网络Fig.2 Integrated logistics network

接下来进行集成网络优化。过程如下：

步骤1 根据Floyd算法，得出初始成本代价矩阵C0(i,j)(表2)、前驱节点矩阵P0(i,j)(表3)、正向物流设施运营成本数组F[i]={5,4.5,2,1,1,1,1,1}、逆向物流设施运营成本数组R[i]={4,3,1.5,0.5,1,2,2,2.5}。其中，V1→V3的单件成本为正向运输成本与两端节点V1、V3的正向物流设施成本之和，即：5+3+2=10；V3→V1 的单件成本为逆向运输成本与两端节点V1、V3的逆向物流设施成本之和，即：1.5+3+4=8.5；同一节点间不发生位移，成本为 0；因为同一层级的节点间不发生联系，故它们之间的运输成本为无穷，比如V1→V2，用符号“∝”表示；初始矩阵中，非直接相连的节点间的运输成本因为暂不可达，记为近似无穷，比如V1→V6，用符号“∞”表示。

表2 初始成本代价矩阵C0(i,j)Tab.2 Initial cost cost matrix C0(i，j)

表3 初始前驱节点矩阵P0(i,j)Tab.3 Initial precursor node matrix P0(i,j)

步骤2 按照算法，应该从V1节点开始更新2个矩阵。本例中，由于V1、V2和V6、V7、V8 为网络的起止节点，同层节点之间无连线，且非相邻层之间节点也无连线(与实际的物流系统相符)，故只需考虑从中间层节点V3、V4、V5开始更新矩阵即可。经过中间节点V3更新后，得到了单件成本矩阵C3(i,j)(表4)和前驱节点矩阵P3(i,j)(表5)。

表4 成本代价矩阵C3(i,j)Tab.4 Cost cost matrix C3(i,j)

表5 前驱节点矩阵P3(i,j)Tab.5 Precursor node matrix P3(i,j)

其中，V1→V6的值经过V3节点中转后，更新为15，即V1→V3→V6的值为V1→V3的值10加上V3→V6的值7减去2(V3的运营成本多算了一次)，同时前驱节点矩阵中V1→V6的值更新为3(V3的节点序号)。同理，V6→V1的值经过V3节点中转后，更新为13.5，同时前驱节点矩阵中V6→V1的值更新为3。

步骤3 经过中间节点V4更新后，得到了单件成本矩阵C4(i,j)(表6)和前驱节点矩阵P4(i,j)(表7)。其中，V1→V8的值经过V4节点中转后，更新为14，同时前驱节点矩阵中V1→V8的值更新为4，即V1→V4→V8的值为14，而V1→V3→V8的值为16，根据算法，取小值。

表6 成本代价矩阵C4(i,j)Tab.6 Cost cost matrix C4(i,j)

表7 前驱节点矩阵P4(i,j)Tab.7 Precursor node matrix P4(i,j)

步骤4 经过中间节点V5更新后，得到了单件成本矩阵C5(i,j)(表8)和前驱节点矩阵P5(i,j)(表9)。

表8 成本代价矩阵C5(i,j)Tab.8 Cost cost matrix C5(i，j)

表9 前驱节点矩阵P5(i,j)Tab.9 Precursor node matrix P5(i,j)

根据结果分析，V1→V6的值为12.5(中转节点为V5)，V2→V6的值为13(中转节点为V5)，故于V6而言，最优单件成本12.5,顺序为V1→V5→V6。网络优化结果见表10。

表10 未考虑设施能力限制的优化结果Tab.10 Optimization results that do not take into account facility capacity limitations

步骤5 考虑设施能力限制，给出最终优化结果。我们仅以正向物流为例来加以考虑。我们以末端需求量为基准来考虑流通渠道中的设施能力限制，本例以配送中心V6、V7、V8的处理/需求能力为基准，根据给出的未考虑设施能力限制的优化结果，按照最优单件成本从低到高的顺序对其依次进行分析。根据表10的优化结果，最优单件成本最低为V8，V6和V7的单件成本相同。我们给出2个组合方案，分别为方案1(依次分析V8、V6、V7的需求)和方案2(依次分析V8、V7、V6的需求)。以方案1为例阐述如下：

V8需求量为 20 000 件，未考虑设施能力限制，最优解为V2→V4→V8(单件成本11.5元)，V4无限制，V2能力为 40 000 件，即V2生产能力中的 20 000 件经V4送达V8。V6需求量为 50 000 件，未考虑能力限制，最优路径为V1→V5→V6(单件成本12.5元)，其中，V1无能力限制，V5能力上限为 40 000 件，也即V6的需求中 40 000 件选择最优路径V1→V5→V6，V6需求尚欠 10 000 件。从表8来分析，次优解为V2→V5→V6(单件成本13元)，由于同样经过V5节点，所以此条路径仍然不可行。接下来，从表6分析，V2→V4→V6(单件成本13.5元)为次优解，V4无能力限制，V2生产能力尚余 20 000 件，即V2生产能力中的 10 000 件，经过V4送达V6，也即对于V6而言，流通渠道有2条，分别是V1→V5→V6和V2→V4→V6。V7需求量为 30 000 件，最优解为V2→V4→V7(单件成本12.5)，V2生产能力尚余 10 000 件，经过V4送达V7。V7需求尚欠 20 000 件，从表8可以看出，次优解为V1→V3→V7(单件成本14)，V1和V3均无能力限制，即V1生产 20 000 件经V3送达V7，对于V7而言，流通渠道有2条，分别是V2→V4→V7和V1→V3→V7。方案1的正向物流流通总成本为127万元。

以此类推，方案2的正向物流流通总成本为127万元。即方案1和方案2的总成本相同。具体结果如表11所示。

表11 考虑设施能力限制的正向物流优化结果Tab 11 Results of forward logistics optimization considering facility capacity constraints

3 结 语

正/逆向物流集成的制造/再制造网络中，网络优化的目的就是根据某一方面的考量来选择最优的流通渠道。基于Floyd算法的制造/再制造网络优化，可以基于成本因素，也可以基于时间因素来进行渠道优化。考虑到设施处理能力限制，通常以末端需求量为基准来考虑流通渠道中的设施能力情况，选择符合条件的最优路径。与整数线性规划模型相比，Floyd算法建模简单，算法清晰，可以通过编程将其融入现有的物流信息系统，让系统自动做出选择。