不同应变条件下橡胶颗粒?砂混合土动模量和阻尼比的联合试验研究
2021-09-08刘启菲庄海洋吴琪
刘启菲 庄海洋 吴琪


摘要: 针对共振柱和动三轴两种不同仪器设备的试验性能和已有相关研究存在的问题,采用共振柱和循环三轴联合试验,研究了废弃轮胎粉碎橡胶颗粒?砂混合土在宽剪应变范围内动模量和阻尼比的动力学特性。结果表明:共振柱试验得到的初始动模量明显比动三轴试验结果要大,动三轴试验得到的初始动剪切模量对应的应变幅值较大引起测得的初始剪切模量偏小。采用共振柱获得的初始剪切模量来计算联合试验测得的宽应变范围内动模量比和阻尼比较为合理。同时发现,当剪应变幅值较小时,橡胶颗粒含量越高,混合土的阻尼比越大,主要由橡胶颗粒初始材料阻尼较大引起;当剪应变幅值较大且超过某临界值后,橡胶颗粒材料阻尼比随橡胶含量增加而减小,主要由混合料的应力?应变关系曲线对应的滞回阻尼越小引起。
关键词: 橡胶颗粒?砂混合土; 共振柱试验; 动三轴试验; 动剪切模量; 阻尼比
引 言
中国每年大量的轮胎消费导致产生的废弃轮胎不断囤积,对其处理不当将会对环境造成严重污染,如何对其进行合理的回收再利用已经成为亟待解决的社会问题。将废弃轮胎回收粉碎后得到的橡胶颗粒具有密度轻、压缩性强、耐久性好等优点,将其与回填土混合,可以显著改善土体的物理力学性能,同时起到隔震减振的作用[1]。因此,开展橡胶颗粒?砂混合土的力学特性和工程应用研究,可以很好地解决目前废弃轮胎再利用的社会问题,并降低工程建造成本,是实现土木工程绿色可持续发展的重要途径之一。
对于橡胶颗粒?砂混合土的力学特性,国内外已经开展了一定数量的研究。例如,Tatlisoz等[2]研究了废弃轮胎橡胶颗粒与粗、细粒土混合物的抗剪强度、泊松比、压缩系数等;Nakhaee等[3]通过对橡胶颗粒混合土进行一系列的循环三轴试验研究了橡胶含量和围压对动剪切模量的影响,基于双曲线模型提出了最大剪切模量、归一化剪切模量与围压和配合比的函数关系;Anastasiadis等[4]通过共振柱试验发现橡胶颗粒混合土具有低剪切模量和高阻尼比的特点,给出了在小应变范围内剪切模量和阻尼比的估算公式;Kostas Senetakis等[5]對质量比为0?35%的橡胶?砂和橡胶?砾石干燥混合土进行共振柱试验,指出围压、橡胶含量和粒度特征是影响混合土动力学性能的主要因素;刘方成等[6]通过循环单剪试验得出了不同竖向固结压力下不同配合比橡胶砂的动剪切模量和阻尼比变化规律,并指出试验方法对橡胶颗粒?砂混合土动力学特性的影响不大。
总结已有科研成果,人们对橡胶颗粒混合土动力特性的试验研究主要集中在小应变范围,但地震时土体的剪应变范围约在5×10-6?5×10-3之间,尤其是土体处于破坏状态前,其剪应变甚至超过10-2,明显处于中等变形和大变形阶段[7]。目前,测试土体动力学特性所用的共振柱主要测试应变范围为1×10-6?5×10-4,很难准确测试大应变范围内土体动力学参数,一般通过小应变范围的测试结果经验推导得到大应变范围的动力学参数。然而,常用的动三轴试验仪主要测试应变范围为1×10-3?5×10-2,对小应变范围土体动力学参数的测试结果精度不高。因此,本文采用共振柱和动三轴两种不同应变测试能力的仪器,开展了橡胶颗粒?砂混合土动力学特性的联合试验研究,得到不同橡胶含量的混合土在宽应变范围内动剪切模量比G/Gmax和阻尼比λ与剪应变幅值γa的关系曲线变化规律,初步解释了相关的试验现象,并给出了橡胶颗粒?砂混合土相关动力学参数的建议值。
1 试验仪器及方案
1.1 试验仪器与测试原理
本次橡胶颗粒混合土的动力特性测试通过共振柱试验与动三轴试验相结合的方式进行。共振柱采用美国GCTS公司研制的TSH?100高精度固定?自由型共振柱测试系统,测试系统组成部分包括:(1)压力控制面板及压力控制仓;(2)试样测试平台;(3)数字伺服控制器及采集系统;(4)计算机。如图1(a)所示。试验中对试样顶部施加扭矩进行激振,待土样达到共振频率后停止加载,土样由共振转为自振,通过传感器精确测量试样的剪切应变,利用共振频率测得动剪切模量,利用土样自由振动的衰减得到阻尼比。
动三轴试验采用英国GDS伺服电机控制的动三轴测试系统(DYNTTS),如图1(b)所示,由两台液压控制器分别对压力室中的水压力(围压)和试样反压进行量测和控制,最大可达1 MPa。可独立控制轴向力,进行静/动态加载,可施加最大10 kN、频率为2 Hz的动态荷载。通过底座的升降对试样进行动态加载,并通过位于试样顶部的轴向力传感器和位于试样底部的轴向位移传感器测量记录试样在大应变(1×10-3?5×10-2)范围的动力特性。
1.2 试验材料与试样制备
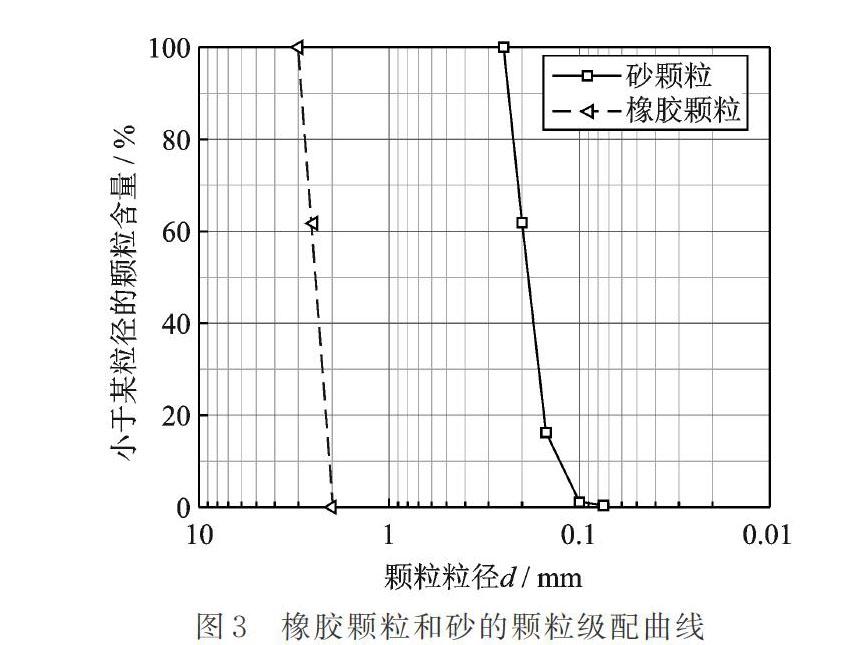
本文试验采用的砂为福建标准砂,颗粒粒径在0.075?0.25 mm之间。橡胶颗粒从专业分解废旧橡胶轮胎的厂家购买,试验中使用橡胶颗粒的粒径dru为2?3 mm,平均粒径D50=2.528 mm,不均匀系数Cu=1.26,橡胶?砂混合土的物理状态如图2所示。橡胶颗粒和砂的级配曲线如图3所示。
共振柱和动三轴试验的试样均为高100 mm、直径50 mm的实心圆柱样。共振柱试验的试样采用冻结制样法[8],将橡胶颗粒和细砂分成四等份,分别加水拌匀(如图2所示),将土样分层装入饱和器后放入饱和缸内饱和30 min。考虑到橡胶混合土在相对密实度较小时试样难以成型,为保证试样的均匀性及形状的规整性,故饱和后冻结进行装样,将底座和承膜筒放入-20 ℃冷冻室冻结3 h。随后迅速将冻样装上仪器并加上相应固结围压统一固结6 h,确保试样完全融化,且样高、体积不再发生变化,即完成固结过程。动三轴试验按《土工试验方法标准》(GB/T 50123?2019)[9]要求采用湿击法制样,共分4层,每层所需橡胶颗粒和福建砂的质量按级配单独配制,控制5%的初始成样含水率,并对试样进行反压饱和固结。
1.3 试验方案与试验加载
根据本次试验目标和相关试验要求,橡胶含量XC按质量比分别取0,10%,20%,30%,40%,50%,70%,100%,控制试样相对密实度Dr=50%,将饱和后的试样进行等向固结,初始有效围压=100 kPa。表1列出了橡胶与砂混合土的基本物理力学参数和具体试验方案。动三轴加载采用应变控制,应变由小到大分20级控制,各级应变加载5个循环,李瑞山等[10]的研究结果表明,在一般地震动的卓越频率范围内,砂土动力特性受振动频率影响不大,故选择加载频率为0.1 Hz,典型加载曲线及对应滞回圈如图4所示。
2 试验结果分析
2.1 动剪切模量和阻尼比
由于两种不同试验的理论基础和试验原理不同,共振柱和动三轴试验直接测得的动力学参数也是不同的。共振柱试验直接推导出橡胶颗粒土在小应变(1×10-6?5×10-4)范围的动剪切模量和阻尼比。动三轴可测得在轴向动应变下的试样动弹性模量和阻尼比,需要通过泊松比将动弹性模量和动轴向应变转化为动剪切模量和动剪应变,根据《地基动力特性測试规范》(GB/T 50269?2015)[11],换算公式为:
式中 Ed为土体的动弹性模量;εd为轴向动应变;νs为泊松比。根据刘方成等[12]对不同配比橡胶砂三轴试验的研究结果表明:不同配比橡胶砂在破坏阶段泊松比趋于0.5,且受围压影响甚小。由于动三轴试验主要记录土体在大应变(1×10-3?5×10-2)范围的动力特性,在此应变范围内,试样基本处于高应力水平状态,故在本文中将泊松比取为0.49。
图5给出了共振柱和动三轴试验联合得到的不同橡胶颗粒掺入量混合土在宽应变范围内动剪切模量随剪应变幅值的变化曲线。从图5可以看出,两种试验得到的橡胶颗粒含量对动剪切模量衰减曲线的影响规律一致,动三轴试验能对共振柱试验无法获得的大应变范围数据进行较好的补充。根据试验结果,可以将橡胶混合土的模量衰减大致分为三个阶段:在动弹性变形阶段(γa≤10-5),动剪切模量基本保持不变;在动弹塑性变形阶段(10-5≤γa≤5×10-3),动剪切模量随剪应变幅值的增大而急剧降低;在塑性变形阶段(γa≥5×10-3),动剪切模量的衰减逐渐减缓,并趋于零。同时,随着橡胶颗粒含量的增加,动弹塑性变形阶段出现所对应的临界剪应变幅也在增加。可以认为,在动弹性变形阶段,土体内部颗粒还未发生明显错动,土体结构处于稳定状态,故其动剪切模量基本保持不变;当橡胶含量增加时,由于橡胶颗粒弹性变形能力强,首先由橡胶颗粒通过发生形变消耗能量,故橡胶颗粒掺入量越多,其模量出现明显衰减对应的剪应变幅越大。
根据试验结果,橡胶颗粒掺入量对于混合土动力特性的影响较大,初始阻尼比随橡胶颗粒掺入量的增加而增大,且阻尼比随剪应变幅值的增长趋于平缓。当剪应变幅值增大到某个值后,阻尼比增长曲线随着橡胶颗粒掺入量的增加而出现降低的现象。可以认为,当剪应变幅值较小时,因橡胶颗粒的初始材料阻尼大于砂土,且该变形范围内以混合土的弹性变形为主,橡胶颗粒含量的增加将明显增大混合土的初始材料阻尼比。但是,当剪应变幅值较大时,混合土的阻尼比特性主要以应力?应变滞回阻尼为主,初始材料阻尼为辅。因此,当橡胶颗粒含量较少时,混合土将发生较大的塑性变形甚至破坏,橡胶颗粒和砂的混合土主要以应力?应变的滞回阻尼为主;随着橡胶颗粒含量的不断增加,混合土的弹性变形能力增强,导致混合土的塑性变形量减小,从而大大降低其滞回阻尼。为了验证上面的发现,图6给出了动三轴试验中单幅轴向应变ε=0.649%时不同橡胶含量所对应的应力?应变滞回圈。由图6可以发现,在此应变下,橡胶含量越低,其滞回圈越饱满,即其表现出的滞回阻尼比越大,且此时滞回圈形状越不规则,土体产生较大的塑性变形。
另外,从图7可以发现,混合土的初始阻尼比在较小剪应变范围内会基本保持不变。同时,随着橡胶颗粒掺入量的增加,初始阻尼比保持不变对应的剪应变范围也越来越大,超过某剪应变幅值以后混合土的阻尼比才慢慢增长。图7初步给出了临界剪应变幅值随橡胶颗粒含量增加而增大的拟合曲线。
2.2 归一化模量比和阻尼比随剪应变幅值的变化曲线
为定量地描述动剪切模量随剪应变幅值的衰退关系,对动剪切模量G进行归一化处理,得到模量比G/Gmax随剪应变幅值的衰退曲线。其中,根据Hardin[13]等提出的土体骨干曲线的双曲线模型确定Gmax的取值,将动剪切模量倒数与动剪应变幅值近似用直线表示
图8给出了橡胶颗粒含量不同时,根据共振柱和动三轴试验结果分别计算得到的初始动剪切模量。两种试验仪器所得到的初始动剪切模量均随着橡胶含量的增加而减小,且动三轴试验得到的结果较共振柱试验结果小得多,仅约为共振柱的30%?40%。主要原因是因为动三轴试验所能测量的最小应变已超过橡胶颗粒土的弹性应变范围,故认为共振柱试验得到的初始动剪切模量比动三轴试验更接近真实值。在本次试验中,共振柱试验得到的最大剪切模量预测公式如下式
(1)Davidenkov模型和陈国兴等[16]提出的阻尼比经验拟合公式均适用于橡胶颗粒土这种新型土体,并且共振柱与动三轴的试验结果得到的橡胶颗粒含量对归一化模量衰减曲线和阻尼比增长曲线的影响规律一致;
(2)对比两种试验方法所得的模量比衰减曲线,共振柱试验所得的拟合曲线分布于一条较狭长的斜S型条带范围内,而动三轴试验所得到的拟合曲线则较分散地分布在大应变对应的条带范围内,其主要原因是因为动三轴试验所得到的初始动剪切模量偏小,进而导致其G/Gmax结果明显偏大。
为了弥补两种不同试验所对应的应变测试范围的局限,图10为采用两种不同处理方法给出将共振柱和动三轴试验结果相结合得到的模量比和阻尼比随剪应变幅值的变化曲线。其中,图10(a)为将共振柱和动三轴试验分别测得的初始剪切模量Gmax计算得到的G/Gmax和阻尼比的变化曲线,记为方法一;图10(b)为将动三轴和共振柱测得的试验结果统一采用共振柱获得的Gmax进行归一化处理得到的拟合曲线,记为方法二。对比两图可得:
(1)由于动三轴试验单独得到的G/Gmax偏大,方法一所得拟合曲线不能很好地将两种试验的结果统一起来,且在大应变范围内,因初始剪切模量测试值偏小,导致得到的归一化模量比实际值偏大,从而导致两种试验结果联合得到的归一化模量比随剪应变幅值的变化无法很好的衔接,故认为这种处理方法不妥;
(2)基于两种不同试验结果,采用方法二得到的归一化剪切模量衰减曲线在小应变幅范围和大应变幅范围都能很好地拟合两种试验结果,本文认为方法二得到的G/Gmax?γa曲线和λ?γa曲线更为合理。
2.3 拟合参数分析
图11分别给出了单独动三轴、单独共振柱试验、本文方法一和方法二得到的拟合曲线对应的6个拟合参数随橡胶颗粒掺入量的变化。当橡胶颗粒含量为100%(纯橡胶)时,四种拟合方法得到的参数均出现较大波动,不符合变化趋势,可认为此时混合土已不符合一般土体的模量和阻尼比的变化规律,且由于100%橡胶含量的土木工程应用不是很普遍,故在此不进行讨论。
由图11可以看出,虽然所选取的Davidenkov模型和阻尼比经验公式中除λmin外的其余5个拟合参数均没有明确的物理意义,但其随着橡胶含量的变化存在明显的规律,6个拟合参数随橡胶含量的变化规律如下:
(1)不同试验和不同处理方法对阻尼比参数λmin的影响较小,且随橡胶含量的增长呈现指数增长;不同试验和不同处理方法对阻尼比参数λ0的影响较大,总体上根据动三轴试验得到的结果更接近于采用共同Gmax的处理结果,随橡胶含量的增长,参数λ0基本呈线形减小趋势;除采用共同剪切模量的处理方法外,橡胶含量对形状参数β的影响相对较小,总体上当橡胶颗粒含量小于50%时参数β随橡胶颗粒含量增长呈略微减小的趋势;
(2)不同试验和不同处理方法对模量拟合参数A'的影响也相对较小,随着橡胶颗粒含量的增加,总体上参数A'在1左右波动,对橡胶颗粒混合土可采用定值1.0;不同试验和不同处理方法对参数B的影响较大,在同种拟合方法中,随橡胶含量的增大,参数B的变化规律不明显,对橡胶颗粒混合土可以采用定值0.4;对于拟合参数γ0,由于动三轴试验所得的G/Gmax偏大,导致采用动三轴试验结果和方法一得到的参数γ0呈指数增长,而共振柱试验结果和方法二得到的参数随掺入量呈稳定的线性增长。
根据上述的分析表明,采用单独共振柱试验获得的G/Gmax ?γa曲线对应的模型拟合参数与采用共同Gmax的联合试验得到的拟合参数较为接近,即根据共振柱试验得到的G/Gmax?γa曲线基本也能够预测大应变范围内的G/Gmax?γa关系。但是,基于单独共振柱试验结果得到的λ?γa曲线对应的模型参数与采用共同Gmax的联合试验得到的拟合参数相差较大,即非常有必要采用共振柱和动三轴联合试验获得的宽应变范围内λ?γa曲线。
3 模型参数建议值
根据本文的试验结果,认为选取共振柱试验得到的Gmax统一对两种仪器联合试验结果进行归一化处理得到的G/Gmax?γa和λ?γa曲线更为合理。总体上,针对本文研究的橡胶颗粒土,当橡胶颗粒含量改变时,可以认为对G/Gmax?γa曲线的拟合参数A'和B及其λ?γa曲线拟合参数β影响不大,建议采用定值:A'=1.05,B=0.4,β=2.5。但是,橡胶颗粒含量对参考剪应变幅γ0、最小阻尼比λmin和阻尼比曲线参数λ0的影响较大,可用图12中所示的拟合公式反映橡胶颗粒含量对其的影响规律。
4 结论与建议
基于共振柱试验和动三轴试验在测得土体动力学特性方面所具有的不同优势,本文采用动三轴和共振柱两种不同试验仪器开展了不同橡胶颗粒掺入量的橡胶?砂混合土动力学特性的联合试验研究,得到的主要结果和发现如下:
(1)共振柱和动三轴试验均能得到橡胶颗粒土的动剪切模量和阻尼比,且得到的橡胶颗粒含量对混合土动力学特性的影响规律具有一致性,但动三轴试验得到的初始剪切模量比共振柱试验小得多,本文分析认为,单独依据动三轴试验结果计算得出的初始剪切模量Gmax和模量比G/Gmax存在较大误差;
(2)橡胶颗粒混合土的动剪切模量衰减大致可分为三个阶段:①动弹性变形阶段(γa≤10-5),动剪切模量基本保持不变;②动弹塑性变形阶段(10-5≤γa≤5×10-3),动剪切模量随剪应变幅值的增大出现明显衰减;③塑性变形阶段(γa≥5×10-3),動剪切模量的衰减逐渐减缓,并趋于零;
(3)橡胶颗粒混合土初始阻尼比随橡胶颗粒掺入量的增加而增大,但是随着橡胶颗粒含量的增加,橡胶颗粒土的阻尼比增长曲线出现明显的初始平台段,即超过某临界剪应变幅后阻尼比曲线才会明显增长。本文初步给出临界剪应变幅与橡胶掺入量的经验关系;
(4)当剪应变幅较小时,因橡胶颗粒的材料阻尼大于砂粒,且该变形范围内以混合土的初始材料阻尼特性为主,橡胶颗粒含量的增加将明显增大混合土的阻尼比。但是,当剪应变幅值较大时,混合材料以应力?应变的滞回阻尼特性为主,随着橡胶颗粒含量的增加,混合土的弹性变形能力越好,滞回阻尼越小,从而降低了混合土的阻尼比;
(5)采用单独共振柱试验获得的G/Gmax?γa曲线对应的模型拟合参数与采用共振柱试验得到的Gmax进行联合处理两种不同试验测得的宽应变范围内试验结果得到的模型拟合参数较为接近,即根据共振柱试验得到的G/Gmax?γa曲线基本也能够预测大应变范围内橡胶颗粒土的G/Gmax?γa关系。但是,基于单独共振柱试验结果得到的λ?γa曲线对应的模型参数与采用共同Gmax的联合进行联合处理两种不同试验得到的拟合参数相差较大;
(6)基于福建标准砂细砂与橡胶颗粒得到的混合料的试验结果,认为采用基于共振柱试验获得的Gmax处理两种不同试验获得的G/Gmax?γa曲线和λ?γa曲线更为准确,本文初步给出了针对此种粒径混合土在不同橡胶颗粒掺入量的G/Gmax?γa和λ?γa曲线拟合参数建议取值。
参考文献:
[1] Zhang T G L S. Laboratory observation of engineering properties and deformation mechanisms of cemented rubber-sand mixtures[Z]. 2016: 120, 514-524.
[2] Tatlisoz Na, Benson C H, Edil T B. Effect of fines on mechanical properties of soil-tire chip mixtures[C]. Testing Soil Mixed with Waste or Recycled Materials, American Society for Testing and Material, 1997, 1997(1275): 93-108.
[3] Nakhaee A, Marandi S M. Reducing the forces caused by earthquake on retaining walls using granulated rubber-soil mixture[J]. International Journal of Engineering, Transactions B: Applications, 2011, 24(4):337-350.
[4] Anastasiadis A, Senetakis K, Pitilakis K. Small-strain shear modulus and damping ratio of sand-rubber and gravel-rubber mixtures[J]. Geotechnical and Geological Engineering, 2012, 30(2): 363-382.
[5] Senetakis K A A A. Dynamic properties of dry sand/rubber (SRM) and gravel/rubber (GRM) mixtures in a wide range of shearing strain amplitudes[Z]. 2012: 33, 38-54.
[6] 劉方成,陈璐,王海东.橡胶砂动剪模量和阻尼比循环单剪试验研究[J].岩土力学, 2016, 37(7): 1903-1913.
LIU Fang-cheng, CHEN Lu, WANG Hai-dong. Evaluation of dynamic shear modulus and damping ratio of rubber-sand mixture based on cyclic simple shear tests[J]. Rock and Soil Mechanics, 2016, 37(7): 1903-1913.
[7] 张克绪,谢君斐?. 土动力学[M].北京:地震出版社, 1989: 276.
ZHANG Ke-xu, XIE Jun-fei. Soil Dynamics[M]. Beijing: Seismological Press,1989: 276.
[8] 李晓雪, 庄海洋, 张沁源, 等. 橡胶颗粒土动剪模量与阻尼比的共振柱试验研究[J]. 防灾减灾工程学报, 2019, 39(2): 265-271.
LI Xiaoxue, ZHUANG Haiyang, ZHANG Qinyuan, et al. Experimental study on dynamic shear modulus and damping ratio of rubber-sand mixed soil[J]. Journal of Disaster and Mitigation Engineering, 2019, 39(2): 265-271.
[9] 中华人民共和国水利部. GB/T 50123-2019,土工试验方法标准[S].北京:中国计划出版社,2019.
Ministry of Water Resource of the People's Republic of China. GB/T 50123-2019, Standard of geotechniced teoting method[S]. Beijing: China Planning Press, 2019.
[10] 李瑞山, 陈龙伟, 袁晓铭, 等. 荷载频率对动模量阻尼比影响的试验研究[J]. 岩土工程学报, 2017, 39(1):71-80.
LI Rui-shan, CHEN Long-wei, YUAN Xiao-ming.et al. Experimental study on influences of different loading frequencies on dynamic modulus and damping ratio [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1):71-80.
[11] 中国机械工业联合会.GB/T 50269-2015,地基动力特性测试规范[S].北京:中国计划出版社,2015.
Machinery Industry Federation. GB/T 50269-2015, Code for measurement methods of dynamic properties of subsoil[S]. Beijing: China Planning Press, 2015.
[12] 刘方成, 吴孟桃, 刘娜,等. 橡胶砂泊松比试验研究[J]. 岩石力学与工程学报, 2017,36(S1):483-493.
LIU Fang-cheng, WU Meng-tao, LIU Na, et al. Experimental study on Poisson's ratio of rubber-sand mixtures [J]. Chinese Journal of Rock Mechanics and Engineering, 2017,36(S1):483-493.
[13] Hardin B O, Drnevich V P. Shear modulus and damping in soils: Design equations and curves[C]. United States: American Society of Civil Engineers, 2002.
[14] 胡聿贤. 地震安全性评价技术教程[M]. 北京:地震出版社, 1999.
HU Yu-xian. Seismic Safety Evaluation Technology Tutorials[M]. Beijing: Seismological Press,1999.
[15] Martin P P, Seed H B. One-dimensional dynamic ground response analyses [J]. Journal of the Geotechnical Engineering Division, 1982, 108(GT7): 935-952.
[16] 陈国兴,刘雪珠,朱定华,等. 南京新近沉积土动剪切模量比与阻尼比的试验研究[J]. 岩石工程学报, 2006, 28(8):1023-1027.
