工业机器人重载下关节变形补偿
2021-09-08毛晨涛张翔祖洪飞
毛晨涛 张翔 祖洪飞


摘要: 传统校准方法只能辨识空载工况下机器人杆件及关节误差,当机器人在大负载工况下由于变形会导致末端精度显著下降。提出了大负载机器人在重载条件下关节变形的模型,通过激光跟踪仪测量辨识机器人关节刚度系数,并优化控制律设计。该方法基于指数积(POE)模型和微分误差模型,在空载工况下计算出结构参数,零位误差,将补偿结果写回机器人控制器;在满载条件下基于之前的坐标准直,辨识机器人关节刚度系数,完成校准过程。本算法在新松、埃斯顿等多家机器人公司的产品上进行了验证。结果表明:该校准方法能够使大负载机器人在重载工况下的绝对定位精度与空载工况下接近。
关键词: 工业机器人; 刚度辨识; 关节变形; 重载; 指数积
引 言
工业机器人的零部件在加工装配过程中不可避免地会引入杆长、零位等结构参数误差,通常的解决方法是通过测量机器人末端的定位误差来辨识其结构参数,通过结构参数校准能够极大地提升机器人性能,其绝对定位精度指标通常能够达到1 mm以内[1?4]。然而通过大量试验发现,机器人在大负载工况下,由于关节的变形,只通过结构参数校准并不能很好地提升机器人精度。通过辨识各关节的刚度系数,补偿由于变形导致的关节角度偏差,可以有效提升机器人在重载条件下的绝对定位精度。通常焊接、激光切割和喷涂等机器人末端都会加载大负载工装,同时这些操作对机器人的绝对精度要求比较严格,所以对大负载机器人的关节刚度系数辨识是很必要的。对于工业机器人的刚度校准,国内外提出了很多理论和方法,如通过机器人三维模型进行有限元分析得到末端的变形量[5];对电机?减速器?连杆的变形?力矩关系建立了数学传递模型[6];基于CCT理论将机器人末端所受力?力矩分解到各个关节上,分析变形?力矩关系[7?10];包含平衡缸的机器人刚度校准等[11]。但是先前研究大部分都是基于理论计算得到机器人各关节克服末端及自身重力所要提供的力矩,而这部分力矩没有考虑克服减速器齿轮之间的摩擦力所要提供的力矩,使得最后计算得到的刚度系数偏小;而且之前的研究大部分都基于机器人的DH模型,当前后两关节平行时DH模型会存在奇异的问题。
机器人建模理论方面,Denavit?Hartenberg首先提出了DH模型,该模型能够使用最小参数集表示各关节坐标系。Hayati通过引入绕y轴旋转的冗余参数消除DH模型中的奇异性问题,提出了MDH模型[12]。之后,Brockett提出基于指数积(POE)的机器人模型也很好地解决了DH模型中存在的奇异性问题[13],而且更直观地描述了关节角度和末端位姿变化的关系。Li等基于POE模型对SCARA機器人误差进行了辨识[14]。之前还没有学者使用POE模型对机器人刚度参数进行辨识。
通过上述分析,本文基于POE模型,考虑机器人空载下几何构型误差及重载下的关节变形误差,建立机器人的误差微分模型、测量并分析点位数据、辨识出相关误差量并对控制器参数补偿以提升机器人绝对定位精度性能。本文提出的算法通过试验验证了刚度系数辨识和变形补偿方法的有效性。
1 机器人校准问题描述
1.1 机器人-传感器系统
机器人测量系统搭建如图1所示,其中机器人末端实到位置通过激光跟踪仪测量安装在机器人末端的靶标球得到。本试验所采用的测量设备是Faro Vantage激光跟踪仪(精度为10 μm+2.5 μm/m),试验对象是新松的重载机器人SR210(最大负载为210 kg)。大负载机器人通常使用RV减速器进行减速增矩,其传动齿轮表面通常进行修形或硬化处理。通过大量试验发现当机器人负载较小时,减速器扭转变形可以忽略不计。而在大负载工况运动时,减速器变形处于近似线性的区域。
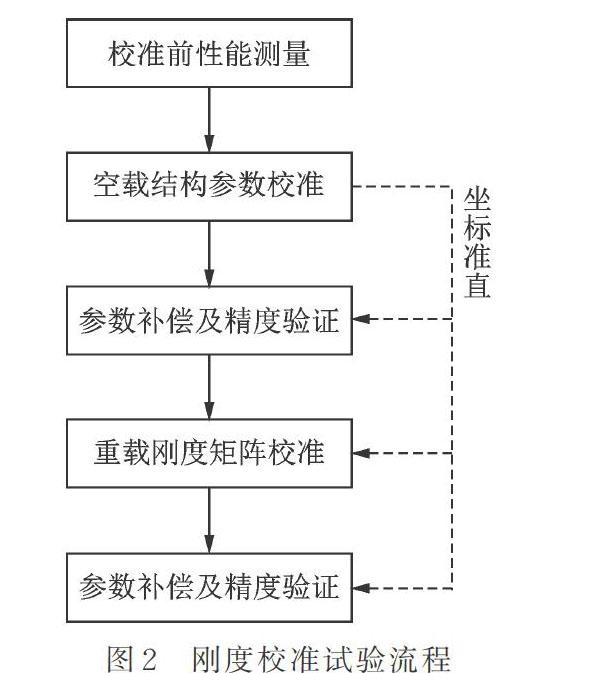
基于以上分析,分两步分别对机器人结构参数和刚度系数进行辨识,其测试流程如图2所示。空载结构参数校准时,机器人末端依次运动到笛卡尔空间的任意50个位型,测量并记录下其位置数据及相应的关节角度值,辨识得到测量坐标到基坐标系的坐标转换矩阵,机器人杆长零位等结构参数值和工具中心点坐标值。将机器人在空载条件下辨识得到的结构参数补偿回机器人控制器,然后在机器人末端加上210 kg质量块;同样地,机器人运动到之前的50个位型,记录各个位型对应的末端位置信息、关节角度值和各关节的电流值,辨识得到各关节由于负载变形的刚度系数。
由于测量坐标系到机器人基坐标系的坐标转换是未知的,需要辨识坐标转换矩阵进行坐标对齐。本文将空载结构参数辨识得到的坐标准直作为后续性能测量与刚度校准的基准,用于对比验证校准前后的精度提升情况。
1.2 机器人前向运动学
考虑一个n自由度的串联机器人,其末端点在笛卡尔空间中可以描述为非线性映射关系
式中 映射f()描述了关节角度值θ,待辨识参数x到机器人末端位置P的关系。由Brockett提出的应用于机器人运动学POE模型,基于旋量理论和线性代数将每个关节轴以旋量的形式表达在空间中。由于POE模型从几何结构参数微分空间到模型参数微分空间是连续映射关系,能够避免DH模型存在奇异的问题,同时也更直观地描述末端误差与关节角度误差的关系,所以本文基于POE模型对机器人进行建模。根据POE参数模型的定义,在测量坐标系下表示的机器人末端坐标为
式中 M为从测量坐标系到机器人基坐标系的坐标变换,,为机器人各轴关节角,为各关节的旋量表示,为在零初始条件下从机器人基坐标到末端坐标的齐次变换。
1.3 校准问题描述
机器人校准问题可视为以末端绝对定位误差为目标函数的优化问题,不断搜索得到使定位误差减小的结构参数解。将多组测量并计算得到的定位误差描述为最小二乘误差形式,则目标函数可写为
式中 向量r为m组位型对应的机器人末端定位误差序列,为第j组位型对应的机器人末端位置测量值。对于结构参数校准问题,待辨识参数x表现为机器人杆长零位等参数;对于刚度系数校准问题,待辨识参数x表现为各个关节的刚度系数。
2 校准问题的求解
通过上一部分对机器人校准问题的分析,将其抽象为一个最小化优化问题。下面结合机器人运动学相关理论,对上述校准问题进行求解。
2.1 结构参数校准
高斯?牛顿法使用泰勒展式近似代替非线性回归模型公式,不断迭代使待辨识参数逼近非线性回归模型的真实值。其迭代过程可以表示为
2.2 刚度系数校准
通过先前学者的研究,发现机器人杆件刚度系数远大于机器人关节刚度。同时,由于机器人控制的实时性需要,补偿关节角度变形更容易实现。所以,只考虑机器人电机?减速器?连杆重载变形中减速器的变形。直流伺服电机的电磁特性公式为
式中 为电机的输出力矩,为电机电势常数,为磁通量,I为电机的控制电流,其可以直接从机器人的控制器中读取。将减速器作为研究对象,作用在各关节的力矩关系如下式所示
从上式可以看到各关节的输入力矩不仅要克服自身的等效重力矩,还要克服减速器之间的摩擦力矩和加载在末端的力?力矩等效在各关节上的力矩。由于在静止条件下进行测试,所以不存在科氏离心力矩和。先前的研究对关节刚度系数辨识时只考虑了自重力矩和外力矩,而忽略了存在非线性的摩擦力矩,导致计算理论力矩时存在误差。注意到电机的输出力矩等于减速器的输入力矩,直接读取伺服电机的电流值计算减速器克服外力矩的等效力矩,可以更精确地辨识刚度系数。
将减速器近似为线性扭簧模型,杆件近似为刚体,则减速器的角度变形量与输入力矩成正比。减速器的输入力矩与变形量存在以下关系。
3 实验验证与结果分析
3.1 结构参数解耦
对于六转动关节机器人,结构如图3所示。
3.2 刚度系数辨识与补偿
如图4所示,通过在机器人末端加载力?力矩,使机器人的关节产生变形。使用跟踪仪测量机器人末端的定位误差,通过控制器读取各关节电流值及相应的关节角度,可以辨识出柔度系数向量。
3.3 实验过程及结果
机器人空载校准结果如表1所示,结构参数校准前后的精度如图6所示,可以看到经过结构参数的校准,机器人的绝对定位精度从2.36 mm提升到0.82 mm,精度提升了65.25%。
机器人满载校准结果如表2所示,刚度系数校准前后的精度如图7所示。经过刚度系数校准,机器人的绝对定位精度从10.09 mm提升到2.42 mm,精度相对于结构参数校准的结果提升了76.01%。
有一点需要说明,由于本实验设计的过程中只加载了重力负载,重力方向与机器人第一转轴的方向一致,根据机器人静力学的理论可知,重力分解到第一转轴的力矩为0,从实验的数据上也可以验证第一轴的电机控制电流很小。由于第一轴减速器输出力矩几乎为0,所以不对第一轴的柔度系数进行辨识。同样地,从图1可以看到,末端加载的质量负载是中心对称的,所以第六轴的输出力矩也几乎为0,所以也不对第六轴的柔度系数进行辨识。
为了进一步验证刚度校准的效果,根据GB12642对机器人选定工作立方体中的5个点进行性能测量验证,验证的结果如图8和表3所示。刚度校准能够极大地提升重载时机器人末端的绝对定位精度,但精度还是略低于空载结构参数校准后的数据;在空载状态下对刚度参数进行校准,绝对定位精度的结果却下降了,原因可能是在空载状态下减速器的齿轮变形不明显,还处于硬化区域,在重载辨识的刚度系数并不适用于空载的情况。
对图8中空载减速器齿轮变形处于硬化区域进行进一步研究,验证不同负载率条件下辨识的刚度系数的适用情况。不同负载率条件下补偿的刚度系数均是在机器人满载情况下辨识得到的。实验结果如表4所示,可以看出当负载率达到25%以上,对关节变形补偿后,机器人末端的位置准确度与距离准确度都有明显提升,满载时补偿效果最好。
4 结 论
本文通过建立基于POE理论的微分运动误差模型,对空载工况下的机器人结构参数进行校准,得到坐标准直和工具TCP信息,在满载工况下对机器人各个关节的刚度系数进行辨识,补偿回机器人控制器,进而提高机器人的绝对定位精度。该算法有以下优势:
(1)基于机器人POE模型,从几何结构参数微分空间到模型参数微分空间是连续映射关系,避免了DH模型位型奇异性的问题;
(2)先前学者研究基于POE模型的校准只修正旋量的误差,而旋量误差不能与机器人的结构参数对应补偿回控制器,本文引入解耦矩阵B分离各个结构参数,使得校准结果能够直接提升机器人性能;
(3)激光跟踪仪能够方便采集机器人末端位置,对于机器人厂家而言,固定机型的机器人跑两遍50个点的位置,就能完成结构参数与刚度参数的校准,整体校准时间可以缩减至20 min,极大地提高生产效率,节约人力成本;
(4)本算法极大地提升了机器人重载工况下的绝对定位精度,使得机器人即使在较大負载情况下(如汽车制造业)也能满足生产需求。
该算法没有考虑机器人杆件变形对末端绝对定位精度的影响,绝对定位精度还有进一步提高的空间。
参 考 文 献:
[1] Nubiola A, Bonev I A. Absolute robot calibration with a single telescoping ballbar[J]. Precision Engineering, 2014, 38(3): 472-480.
[2] Nubiola A. Calibration of a serial robot using a laser tracker[D]. Montreal: ?cole de Technologie Supérieure, 2011.
[3] Nubiola Albert, Bonev Ilian A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29: 236-245.
[4] KUU Y Y, CHEN J J, WANG C C. An automated robot calibration system based on a variable DH parameter model[C]. Proceedings of the 35th Conference on Decision and Control, 1996: 881-886.
[5] 覃欢欢. 6R工业机器人整体刚度建模与弹性动力学分析[D]. 武汉:华中科技大学, 2013.
Qin Huanhuan. Stiffness modeling and viscoelastic dynamic analysis of 6R industrial robot[D]. Wuhan: Huazhong Unversity of Science and Technology, 2013.
[6] Ahmad S. Analysis of robot drive train errors, their static effects, and their compensations[J]. IEEE Journal of Robotics and Automation, 1988, 4(2):117-128.
[7] Chen Shih-Feng. Conservative congruence transformation for joint and cartesian stiffness matrices of robotic hands and fingers[J]. The International Journal of Robotics Research, 2000, 19(9):835-847.
[8] Chen S F. The 6×6 stiffness formulation and transformation of serial manipulators via the CCT theory[C]. IEEE International Conference on Robotics & Automation, 2003:4042-4047.
[9] Alici G. Enhanced stiffness modeling, identification and characterization for robot manipulators[J]. IEEE Transactions on Robotics, 2005, 21(4):554-564.
[10] Dumacs C, Caro S, Chérif M, et al. A methodology for joint stiffness identification of serial robots[C]. 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2010.
[11] Kun Yang. A new methodology for joint stiffness identification of heavy duty industrial robots with the counterbalancing system[J]. Robotics and Computer-Integrated Manufacturing, 2018, 53:58-71.
[12] Hayati S A. Robot arm geometric link parameter estimation[C]. Proceedings of 1983 IEEE Conference on Decision and Control, 1983: 1477-1483.
[13] Brockett R W. Robotic manipulators and the product of exponentials formula[J]. Math. Theory Network Syst., 1984: 120-129.
[14] Li C, Wu Y, Li Z. Identifiability and improvement of adjoint error approach for serial robot calibration[C]. IEEE International Conference on Robotics and Automation. IEEE, 2014:1361-1366.
A joint deformation compensation method for heavy-load industrial robots
MAO Chen?tao1, ZHANG Xiang2,4, ZU Hong?fei3, CHEN Zhang?wei1
(1.State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China; 2.Computer and Softwere School, Hangzhou Dianzi University, Hangzhou 310018, China; 3.School of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China; 4.Zhejiang Premax Technologies, Ningbo 315000, China)
Abstract: The traditional robot calibration method can only identify the errors of geometric parameters under no-load conditions. When the robot is deformed under heavy load conditions, the positioning accuracy is significantly reduced. This paper proposes a model of joint deformation for robots under heavy load conditions, the robot joint stiffness matrix is identified by the laser tracker and the control law design is optimized. Based on the POE model and the differential error model, the structural parameters are calculated under no-load conditions, and the result is written back to the robot controller. Under the heavy load conditions, the robot stiffness matrix is identified based on the previous transformation. The algorithm has been verified on the products of many robot companies. The results show that the calibration method can improve the absolute positioning accuracy of large load robots under heavy load conditions.
Key words: industrial robot; stiffness identification; joint deformation; heavy load; product of exponentials (POE)
作者簡介: 毛晨涛(1993-),男,博士研究生。电话:13606629086; E-mail: mct@zju.edu.cn
通讯作者: 陈章位(1965-),男,教授,博士生导师。电话:13805793651; E-mail: chenzw@zju.edu.cn
