多参考最小二乘复频域法的数值问题分析及优化
2021-09-08章国稳汤宝平陈卓
章国稳 汤宝平 陈卓

摘要: 分析多参考最小二乘复频域法在实际应用中的数值问题,提出一种多参考最小二乘复频域优化方法。由于实际系统阶次未知,为了避免模态遗漏,需先过估计系统阶次。通过理论与数值分析发现:由于系统阶次过估计,识别过程需要对奇异矩阵进行伪逆计算,伪逆计算方法和参数的选择对识别结果有很大影响。利用特征值分解计算奇异矩阵Ro的伪逆矩阵,通过奇异值分解计算奇异矩阵Msub的伪逆矩阵,以能量为指标自动确定阶次,在不失精度的前提下可自动得到清晰稳定图。利用优化多参考最小二乘复频域法对一个7自由度线性时不变系统和葡萄牙Infante D. Henrique大桥辨识,实验结果表明本文方法可以在保持精度的前提下容易地识别系统模态。
关键词: 模态分析; 多参考最小二乘复频域法; 特征值分解; 奇异值分解; 稳定图
引 言
20世纪90年代,针对频域识别中数值病态问题,Guillaume等提出了最小二乘复频域法[1];后来通过使用右矩阵分式模型代替公分母模型改进了识别模型,提出了多参考最小二乘复频域法(本文简称为p_LSCF)[2],在LMS的Test. Lab系统[3]中被称为PolyMAX。该方法具有较为清晰的稳定图,易于实现参数自动识别,识别精度高,被广泛应用于各种领域[4?5]。
由于实际系统阶次未知,为了避免模态遗漏,通常先过估计系统阶次,接着采用稳定图等方式从计算结果中提取系统真实模态[6]。系统阶次过估计导致了计算过程中的部分矩阵为奇异矩阵,而奇异矩阵逆矩阵只能以伪逆矩阵替代。目前伪逆矩阵的计算方式有多种,不同的计算方法以及误差容许设置对识别结果有较大影响。Ro和Msub是p_LSCF中需要求逆的中间矩阵,在系统阶次过估计时为奇异矩阵,而如何确定其伪逆矩阵的最佳估计是一个值得研究的问题。
本文针对p_LSCF计算过程中奇异矩阵的逆矩阵计算问题,提出了一种改进多参考最小二乘复频域法。利用特征值分解计算奇异矩阵Ro的伪逆矩阵,通过奇异值分解计算奇异矩阵Msub的伪逆矩阵,以能量为指标自动确定阶次,可得到清晰稳定图。对一个7自由度线性时不变系统以及葡萄牙Infante D.Henrique大桥进行模态参数识别验证了该方法的有效性。
1 多参考最小二乘复频域法
2 存在的问题分析
由于实际系统的阶次未知,为了不遗漏系统模态,一般先对系统阶次过估计,然后通过稳定图等提取系统真实模态。由于系统阶次过估计,即n大于系统实际阶次,将导致算法识别过程中部分矩阵为奇异矩阵。式(8)在求解矩阵M时需要n+1维方阵Ro的逆矩阵,式(9)在求解a时需要nNi阶方阵Msub的逆矩阵,当n大于系统真实阶次时,Ro和Msub为奇异矩阵,无法得到它们的逆矩阵。因此,需采用它们的伪逆矩阵替代逆矩阵。目前伪逆矩阵的数值计算方法有多种,不同的计算方法和误差容许设置对结果有较大影响。
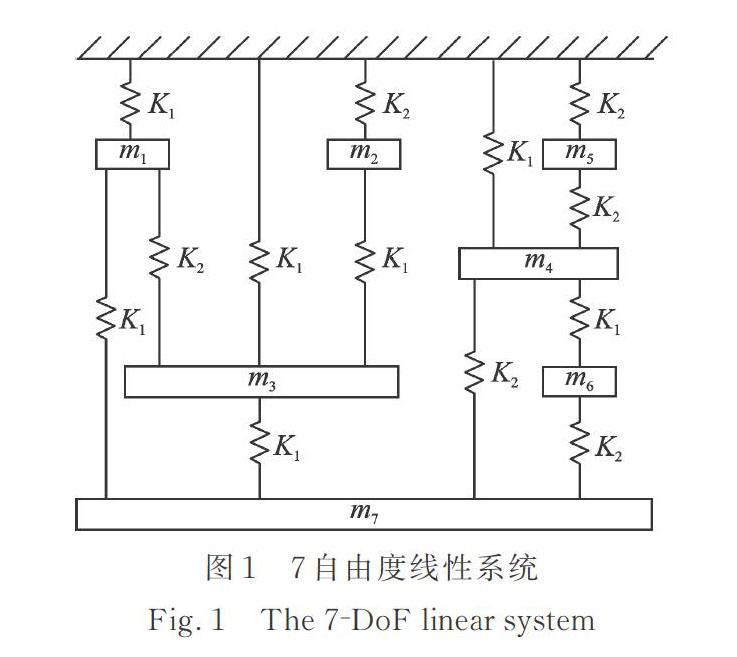
以一7自由度线性时不变系统模态参数识别为例,如图1所示。其中每个质量块的质量都是1 kg,K1=10 kN/m,K2=20 kN/m,阻尼矩阵为C=0.2M+0.0003K,其中M,K分别为系统的质量矩阵、刚度矩阵。依次对各质量块施加脉冲激励,采集每个质量块的速度响应,采样频率为500 Hz,采集时间为50 s,并且在响应信号中含有10%的测量噪声。基于激励响应得到49个频响函数,谱线数为512。本文通过Matlab平台对原p_LSCF进行实现,假设最高阶为50,在计算Ro和Msub的偽逆矩阵时采用Matlab的pinv函数,其中容差Tol分别采用1-1,1-10和1-25。构造稳定图如图2所示,其中,特征频率、阻尼比、模态振型的容差分别为:0.01,0.1,0.02,‘s表示稳定点,‘v表示频率和振型稳定的点,‘d表示频率和阻尼比稳定的点,‘f表示频率稳定的点。
从图2可以看出,在不同容差Tol下,本文将Ro和Msub的容差分别记为TR和TM,原p_LSCF算法得到的结果具有很大差异。当TR和TM都为1-1时,稳定图中只出现了前2阶的极点,剩下5阶模态未识别出;当TR和TM都为1-10时,能较好计算出所有模态;当TR和TM都为1-15时,计算出了大量虚假模态,从中难以提取系统真实模态。算法实现过程中容差的选取对结果影响很大,但由于Matlab的伪逆算法未对外公开,对于实际系统识别过程中的容差选取也没有理论依据,因此难以确定最佳容差参数。针对以上问题,本文对识别过程进行优化。
3 改进多参考最小二乘复频域法
3.1 M矩阵求解
采用本文方法对第2节中的7自由度系统进行分析。计算过程中能量阈值Ethd设为97%,可以看出,在本文方法所得稳定图中系统固有频率形成了稳定轴,并且虚假频率点较少,从中将非常容易获取系统极点。表1为原始p_LSCF(TR=TM=1-10)与本文提出的p_LSCF所得的结果对比。表2给出了不同噪声水平下,两种方法的最大识别误差,可以看出,两种方法识别精度接近。该系统3和4阶以及5和6阶的频率非常接近,从识别结果看出本文方法对密集模态也具有高识别精度。与原始方法相比,本文方法在保持识别精度的前提下可自动得到清晰稳定图,避免人为尝试设置不同参数。在同一台计算机基于Matlab实现两种算法分析以上数据,原始和改进p_LSCF分别需要7.08 s和7.97 s,可见原始和改进p_LSCF具有相似计算量。
4 实例分析
将本文方法应用于葡萄牙InfanteD.Henrique大桥的模态参数识别中,具体描述参考文献[8]。桥梁在环境激励下振动,在桥梁的4个纵向截面上布置了12个加速度传感器,每一纵向截面上布置3个传感器,一个垂直于侧面,另2个垂直于桥面,如图4所示。采样频率为12.5 Hz,对半小时的数据进行分析,即每个通道22500个数据。
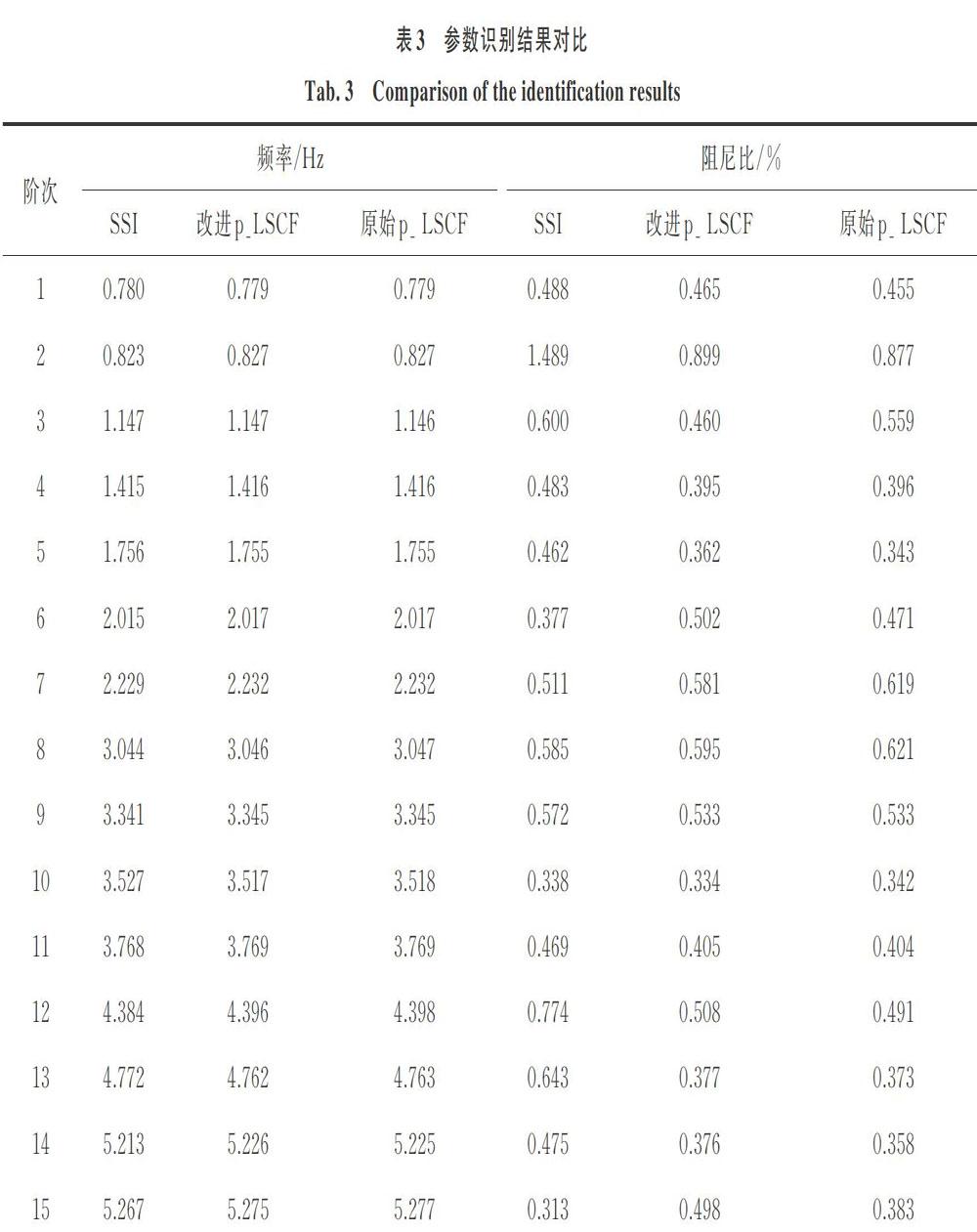
对于环境激励响应分析,采用系统正功率谱密度[9]替代频响函数。为了充分识别所有模态,以所有测点为参考,即Ni=12,No=12,一共可以得到144个正功率谱密度函数,每通道频谱线数为256。假设最高阶为50,采用原始p_LSCF和本文提出的改进p_LSCF分别进行分析并构造稳定图。其中原始p_LSCF经过多次尝试,本文列出三个效果较好的稳定图,如图5所示。可以看出在不同的参数下,识别结果差距很大,其中当TR=1-5,TM=1-25时效果较好,本文采用该结果用以对比分析。图6为本文提出方法的稳定图,结果较为清晰。为了便于参考,本文也采用了COV?SSI方法[10]对数据进行分析,所得结果对比如表3所示。可以看出,三者识别结果总体一致,在阻尼比上差异相对较大(由于数据较小),其中原始p_LSCF与改进p_LSCF结果更接近。从实例分析可知,本文方法在不失精度的前提下可自动得到清晰稳定图,更有利于参数跟踪。在同一台计算机基于Matlab实现算法分析上述数据,原始和改进p_LSCF分别需要27.11 s和31.14 s,可见原始和改进p_LSCF具有相似计算量。
5 结 论
采用多参考最小二乘复频域法对实际结构分析时,通常需要对奇异矩阵Ro和Msub进行伪逆计算,不同伪逆计算方法和参数设置会直接影响识别结果正确性。本文主要针对Ro和Msub伪逆矩阵计算过程进行了优化:1)基于Ro是对称矩阵的特点,采用特征值分解求解Ro伪逆矩阵,根据矩阵特征值确定矩阵的秩;2)在计算Msub伪逆矩阵时,采用奇异值分解计算Msub的伪逆矩阵,根据矩阵奇异值确定矩阵的秩。数值仿真和实例分析表明,相比于原始方法,本文方法在保持识别精度的前提下可得到更清晰稳定图,能更加容易和可靠地识别系统模态。
参考文献:
[1] Guillaume P, Verboven P, Vanlanduit S. Frequency-domain maximum likelihood identification of modal parameters with confidence intervals[C]. Proceeding of ISMA 23, 1998.
[2] Guillaume P, Verboven P, Vanlanduit S, et al. A poly-reference implementation of the least-squares complex frequency domain estimator[C]. Proceeding of the 21st International Modal Analysis Conference, Kissimmee, USA, 2003.
[3] LMS International. The LMS Theory and Background Book[M]. Leuven, Belgium, 2000.
[4] Lin Chang-Sheng. Frequency-domain approach for the parametric identification of structures with modal interference[J]. Journal of Mechanical Science and Technology, 2019,33 (1): 4081-4091.
[5] 石海榮,赵海峰,周国强. PolyMAX法在自升式平台模型损伤检测中的应用[J].机械设计与制造工程,2016,45(3):93-97.
Shi Hairong, Zhao Haifeng, Zhou Guoqiang. Application of PolyMAX method in the damage detection of offshore platform[J]. Machine Design and Manufacturing Engineering,2016,45(3):93-97.
[6] Zhang Guowen, Ma Jinghua, Chen Zhou, et al. Automated eigensystem realisation algorithm for operational modal analysis[J]. Journal of Sound and Vibration, 2014,333 (15): 3550-3563.
[7] Rolain Y, Pintelon R, Xu K Q, et al. Best conditioned parametric identification of transfer function models in the frequency domain[J]. IEEE Transactions on Automatic Control, 1995, 40(11): 1954-1960.
[8] Magalhaes Filipe, Cunha Alvaro, Caetano Elsa. Online automatic identification of the modal parameters of a long span arch bridge[J]. Mechanical Systems and Signal Processing, 2009,23(2): 316-329.
[9] Peeters B, Van der Auweraer H, Vanhollebeke F, et al. Operational modal analysis for estimating the dynamic properties of a stadium structure during a football game[J]. Shock and Vibration, 2007,14(4): 283-303.
[10] Reynders E, Pintelon R, De Roeck G. Uncertainty bounds on modal parameters obtained from stochastic subspace identification[J]. Mechanical Systems and Signal Processing, 2008, 22(4): 948-969.
