基于优化PCNN与区域特征引导法则的图像融合

李 文,叶坤涛,李 晟

(江西理工大学理学院,江西 赣州 341000)

1 引 言

图像融合技术表示为获取同一场景下的多幅传感器图像后,在图像配准基础上采取某种方法融合成一幅对场景信息描述更为清晰、准确的图像[1]。图像融合技术中应用较广的一类为红外与可见光图像融合,红外图像的细节信息丢失较严重,对比度和空间分辨率低,但成像时不受反射光的影响；而可见光图像能够捕获场景中的丰富细节信息,对比度和空间分辨率高,但成像时易受外界环境的干扰。红外与可见光图像融合所形成的融合图像可将二者的优势信息进行互补,获取更全面的场景信息,在目标跟踪、军事、医学和航空等领域均有着重要应用[2]。

当前,图像融合方法一般分为三类,即基于空间域、基于变换域和基于神经网络等其他相关方法。虽然后两类融合方法均属于研究的热点,但第三类方法的参数较多且相关配置较复杂,融合效果也十分依赖相关参数的选取,因此,基于多尺度多方向的变换域方法一直深受研究学者们青睐。从早期的金字塔变换[3]起,一系列的多尺度分析方法相继被研究学者们所提出,如离散小波变换、脊波变换、曲波变换、轮廓波变换、非下采样轮廓波变换(non-subsampled contourlet transform,NSCT)及剪切波变换等[4]。早期的金字塔变换缺乏方向性、融合后的图像冗余度较高,且与离散小波变换、脊波变换、曲波变换、轮廓波变换及剪切波变换均易在图像边缘处产生伪吉布斯现象,从而丢失融合图像的部分边缘信息。NSCT属于轮廓波的改进,虽然能够克服伪吉布斯现象外,具有平移不变性,但计算的复杂度偏高且分解的方向数有限,无法实现对图像的实时处理。

近期由剪切波变换改进而来的非下采样剪切波变换[5](non-subsampled shearlet transform,NSST)得到广泛应用,NSST不仅能够克服图像边缘处的伪吉布斯现象,而且具有平移不变性与各向异性,还具有良好的稀疏表示性能与低计算成本的特点[6],成为应用在于图像融合当中的一种更为理想的多尺度分析方法。研究表明NSST能在红外与可见光图像融合时获取更多的源图像细节信息,但仍存在着融合图像的纹理细节与边缘信息缺失、目标特征不够突出的现象[7-8]。

为了解决上述可见光图像纹理细节与边缘信息缺失、红外目标不够突出问题,同时改善融合图像视觉信息保真度,综合更多的红外与可见光图像优势信息,本文提出一种基于优化脉冲耦合神经网络(pluse coupled neural network,PCNN)与区域特征引导法则的红外与可见光图像融合算法。通过NSST将红外与可见光图像分解为低高频分量,利用图像低高频成分不同的特点,提出优化PCNN模型和区域特征引导法则分别对图像低高频分量进行融合。最后,对融合后的低高频分量进行NSST逆变换获取融合图像。实验对比其他7种传统及流行融合算法,表明了本文算法的优越性与可行性。

2 基本原理

2.1 NSST分解

2007年Guo等[9]在传统的仿射系统基础上结合几何与多尺度变换,构造了剪切波变换。具有合成膨胀的仿射系统MAB(ψ)在空间维数n=2,满足如下条件:

(1)

式(1)中,ψ∈L2(2),L2(2)表示可积空间,通过对基函数ψj,l,k(x)进行旋转、剪切和平移变换来构造仿射系统,A与B为2×2的可逆矩阵,且|detB|=1,A为各向异性膨胀矩阵,B为剪切矩阵,j为分解尺度,l为方向参数,k为平移参数,为整数域。

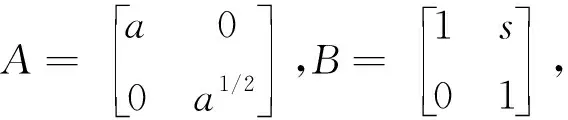
图1为2级NSST分解的示意图。

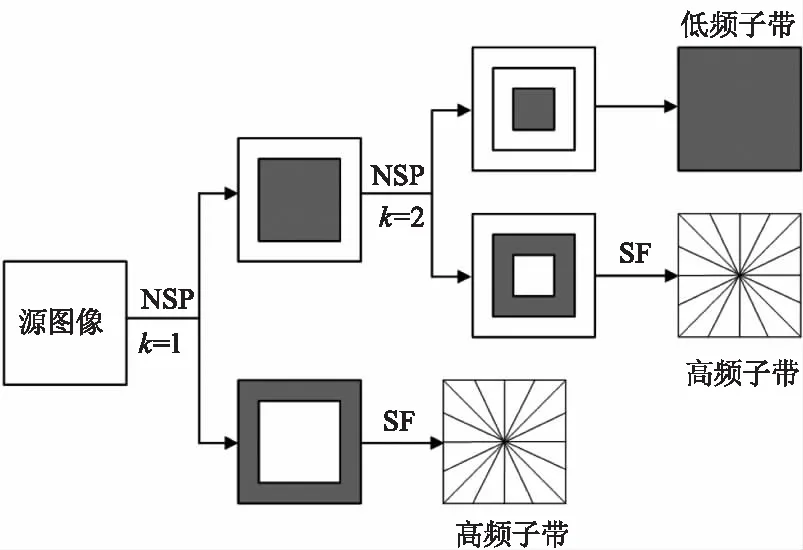
图1 2级NSST分解示意图Fig.1 Schematic two level decomposition of NSST

由图1可知NSST分解主要由非下采样金字塔(non-subsampled pyramid,NSP)分解和方向局部化组成[11]。NSP分解是采用非下采样金字塔滤波器组对源图像进行k级多尺度分解,产生1个低频子带和k个高频子带,k+1个子带图像的尺寸与源图像相同。方向局部化是通过剪切滤波器(shearlet filter,SF)对高频子带进行l级多方向分解,每个高频子带的SF分解都将产生2l个不同方向的子带图像,其尺寸与源图像相同。

2.2 优化PCNN

PCNN称为第三代人工神经网络,是由若干个神经元相互链接形成的二维反馈型神经网络,每个神经元由接收域、调制域和脉冲发生器共三部分组成。目前,PCNN已被广泛运用在图像分割、图像融合及图像细化等方面[12],尤其在与多尺度分析方法相结合进行图像融合时取得突出效果。

PCNN中的每个神经元对应源图像中的每个像素,本文在传统PCNN模型基础上简化,同时对PCNN中的阈值函数进行改进,使图像中较亮像素与较低像素之间的部分处理更为平滑,提出优化PCNN模型,其示意图如图2所示。

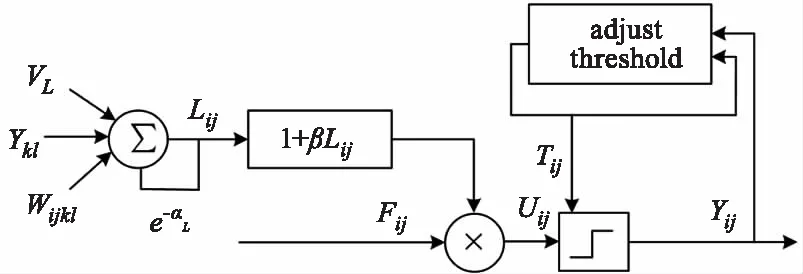
图2 优化PCNN模型Fig.2 Optimized PCNN model

优化PCNN模型对应的数学表达式如下:

Fij[n]=Dij

(2)

(3)

Uij[n]=Fij[n](1+βijLij[n])

(4)

(5)

Tij[n]=Tij[n-1]-Δ+VTYij[n]

(6)

式(2)～(6)中,(i,j)为神经元位置;Fij、Dij、Lij、Uij、Tij分别为神经元的反馈输入、外部输入激励、链接项输入、内部活动项和动态阈值;βij为链接强度;n为迭代次数;(k,l)为神经元的周围连接;αL为链接衰减常数;Δ为阈值衰减因子,用于控制阈值的衰减程度;VL为链接放大系数;VT为阈值放大系数；Wijkl为神经元之间的突触链接权值;Yij为神经元的脉冲输出,其值1或0表示神经元成功点火与否。

Yij为1时,表示神经元成功点火一次。在n次迭代中,计算PCNN输出的点火总次数,作为低频融合系数选取的依据,n次迭代中点火总次数Zij[n]为:

Zij[n]=Zij[n-1]+Yij[n]

(7)

3 本文融合算法设计

本文算法首先对已配准的红外图像A和可见光图像B进行NSST分解,获取相应的低频分量和高频分量。其次,对源图像A和B分解后所获取的低频分量采用优化PCNN模型进行融合,对于高频分量采用区域特征引导法则进行融合。最后,对融合后的低频高频分量进行NSST逆变换,获取融合图像F。图3显示了本文算法的融合过程。

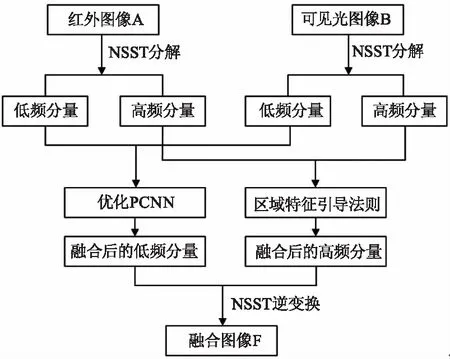
图3 本文算法的融合过程Fig.3 The fusion process of this algorithm

3.1 低频分量的融合规则

NSST分解后的低频分量为源图像的近似成分,包含着图像的主要信息和大部分能量。传统的融合算法为简单加权或取平均的融合规则,这类方法融合后将丢失图像的细节信息,还降低图像的整体亮度,而PCNN能够突出图像的细节部分,同时保留图像的轮廓部分,适用于低频分量融合,因此,本文提出一种基于优化PCNN模型的融合规则进行低频分量融合。

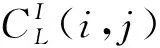
(8)

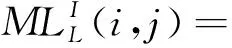
(9)

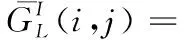
(10)

(11)

式(11)中,β0为初始链接强度,本文使用以往文献的经验取值,取β0=3.0。

基于优化PCNN模型的融合规则,包括以下4步:

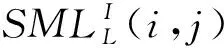
Step2:对优化PCNN模型的参数进行初始化设置,Lij[0]=Uij[0]=Tij[0]=Yij[0]=0,Zij[0]=0,设模型最大迭代次数为Nmax;

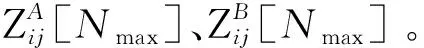
(12)

3.2 高频分量的融合规则

图像的高频分量存储着图像绝大部分纹理细节与边缘信息,反映着图像的突变特性,高频分量融合效果直接关系着融合图像的清晰程度和视觉感官。为了更好地融合高频分量,本文提出利用图像的区域能量、改进空间频率和区域方差匹配度等特征,对图像间的关联性进行分析,提出自适应的区域方差匹配度阈值和调节因子,并将分析结果作为选择不同融合规则的引导信息,由此构造区域特征引导法则对高频分量进行融合。

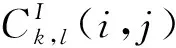
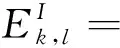
(13)

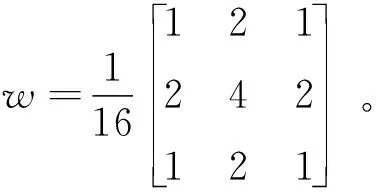
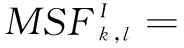
(14)

(15)

(16)

(17)

(18)

(19)

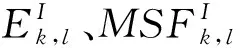
(20)

式(20)中,λ1为红外调节因子;λ2为可见光调节因子,二者满足条件λ1+λ2=1。由于可见光图像相比于红外图像有更丰富的细节信息,而图像的高频部分主要为细节信息,设定可见光调节因子λ2大于红外调节因子λ1,即λ2>0.5,保证融合图像有较多细节信息。

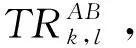
(21)

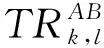
(22)

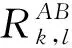
(23)

式(22)～(23)可确保λ2总是大于λ1,保证融合图像有较多细节信息。

确定λ2后,根据λ1+λ2=1获得相应的λ1。本文提出的红外调节因子λ1与可见光调节因子λ2,可以保证融合图像有较多细节信息。

(24)

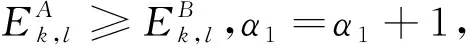
(25)

通过上述区域特征引导法则,完成高频分量的融合。最后,对融合后的低高频分量进行NSST逆变换,获取融合图像F。

4 实验结果与分析

为了验证本文算法的优势与有效性,对多组已配准的红外与可见光图像进行融合实验,实验环境为:Intel Core i5-9750H,CPU主频为2.60GHz,内存16GB,Windows10操作系统,Matlab2019a仿真平台。

实验中,本文算法与LP[3]、CVT[14]、DTCWT[15]、NSCT[16]、NSCT-PCNN[17]、NSST-PCNN[2]、NSST-EOGPCNN[18]共7种融合算法进行了比较,由于篇幅所限,现给出其中3组经典的红外与可见光图像融合结果为例,对8种算法的融合性能进行分析。

图4、图5和图6为上述7种融合算法及本文算法分别对三组红外与可见光图像进行融合所获取的

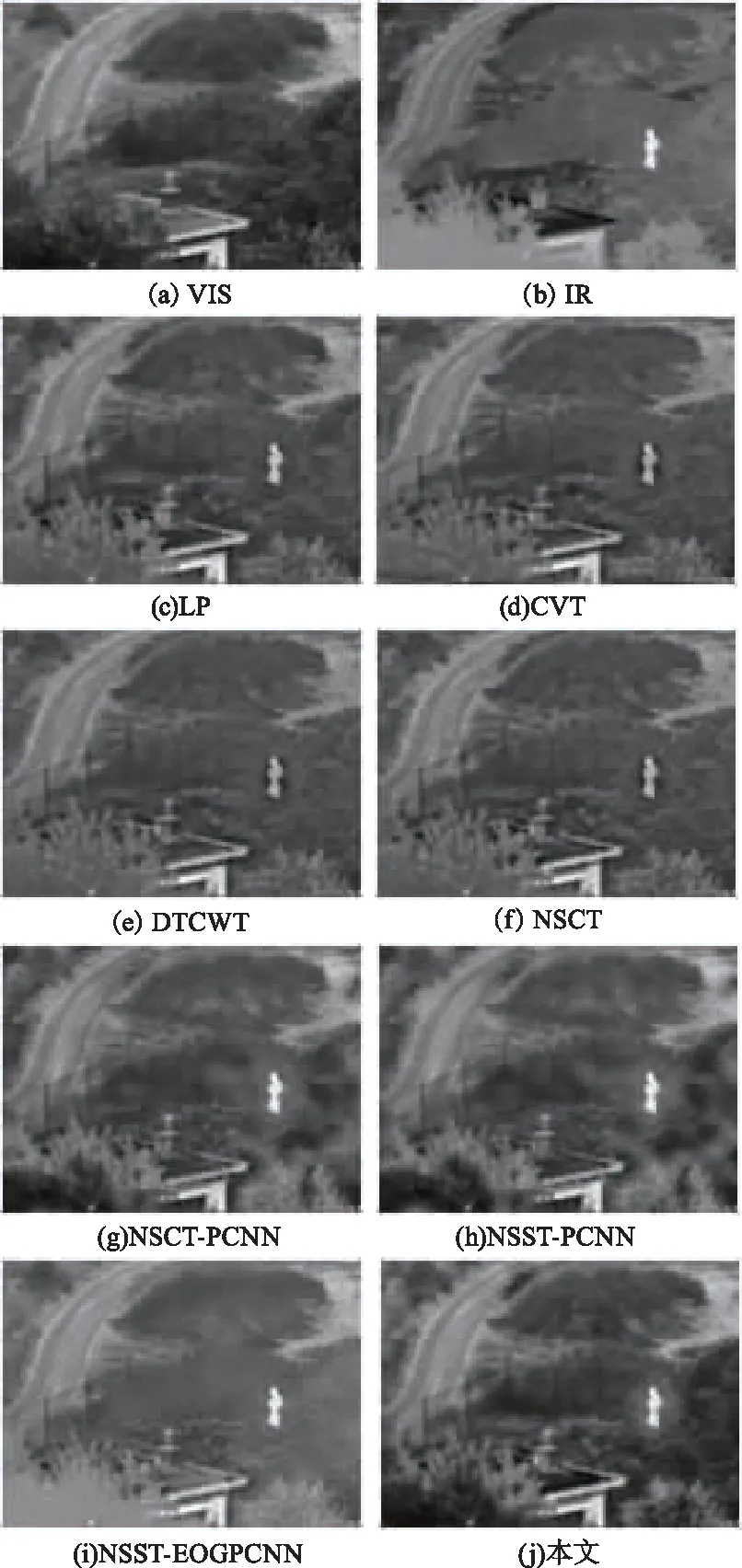
图4 Camp图像的8种算法融合结果Fig.4 Fusion results of eight algorithms of Camp images

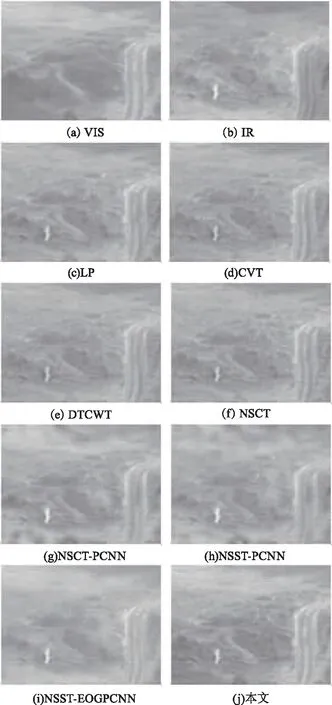
图5 Dune图像的8种算法融合结果Fig.5 Fusion results of eight algorithms of Dune images

融合图像。实验中,本文算法的参数设置为:NSST分解中,选用maxflat为NSST分解滤波器,分解层数为4层,分解方向数为{4,4,8,8}；优化PCNN模型参数设置为:Wijkl=[0.707 1 0.707；1 0 1；0.707 1 0.707]、Nmax=200、αL=1.0、Δ=0.01、VL=1.0、VT=20,β自适应选取。

从主观视觉效果比较图4、图5和图6,发现基于LP算法、CVT算法、DTCWT算法和NSCT算法所获取的融合图像整体偏暗,对比度较低,存在着纹理细节与边缘信息的丢失,同时基于CVT算法、DTCWT算法和NSCT算法的融合图像在人物目标周围有较明显的伪影现象；基于NSCT-PCNN算法和NSST-PCNN算法融合效果较好,能够大体保留图像的人物目标特征和显著信息,但围栏、树木、山路等背景细节信息有部分丢失,山坡轮廓不够清晰；基于NSST-EOGPCNN算法的融合图像整体亮度过高且人物目标较模糊；本文算法的融合图像具有较高的对比度,亮度适中,综合了红外图像与可见光图像各自的有效信息,捕获了更多的纹理细节与边缘信息,人物目标更清晰突出,同时围栏、树木、山坡及山路等背景细节信息保留更完整。由此表明本文算法在主观视觉上优于其他7种融合算法。

图6 Sandpath图像的8种算法融合结果Fig.6 Fusion results of eight algorithms of Sandpath images

同时,本文选取平均梯度AG、空间频率SF、信息熵EN、标准差SD、总体交叉熵RCE和视觉信息保真度VIFF共6项客观指标对7种算法及本文算法的性能进行客观评价。表1、表2和表3为3组经典红外与可见光图像融合时的客观指标结果。由表1～3中的6项客观指标对比分析,发现本文算法仅在RCE上略高于NSCT-PCNN、NSST-PCNN或LP算法,其余5项客观指标均明显优于另外7种传统及流行算法,说明本文算法在6项指标上表现更好,表明了本文算法具有较强的优越性。综合主观视觉和客观指标对比分析而言,本文算法具有明显优于另外7种算法的融合效果,有效地提取融合图像的红外目标特征、同时保留可见光边缘细节信息。

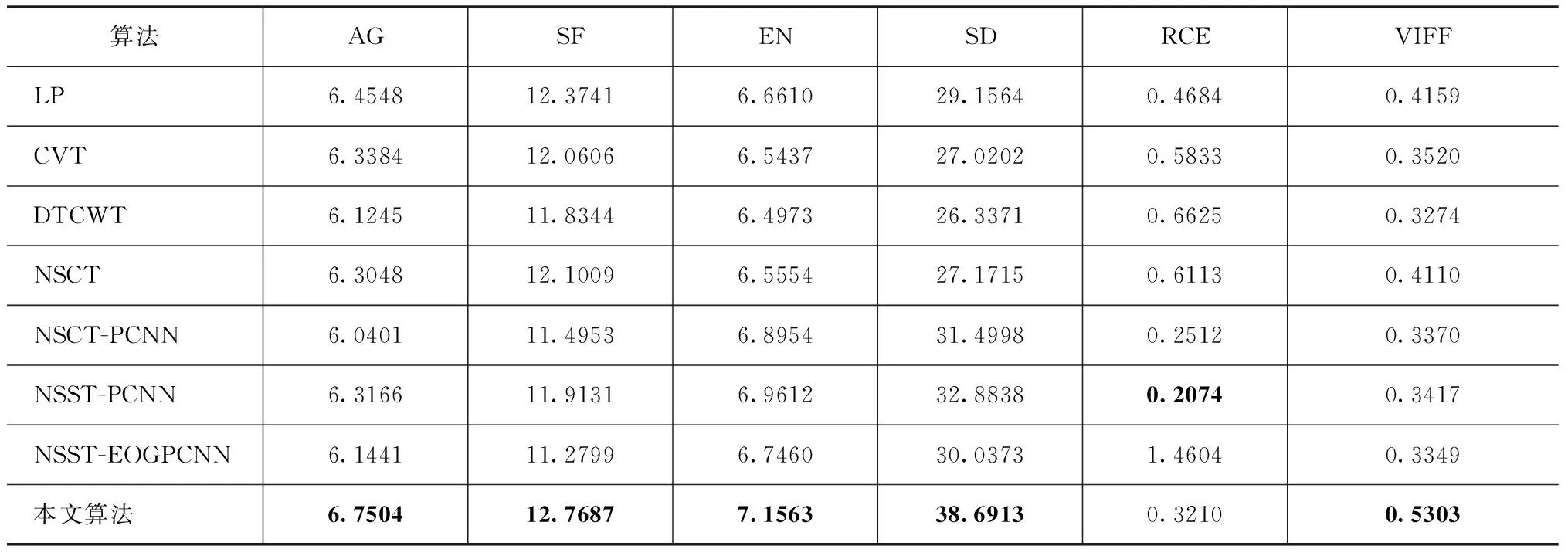
表1 Camp图像融合的客观指标结果Tab.1 Objective index results of Camp image fusion

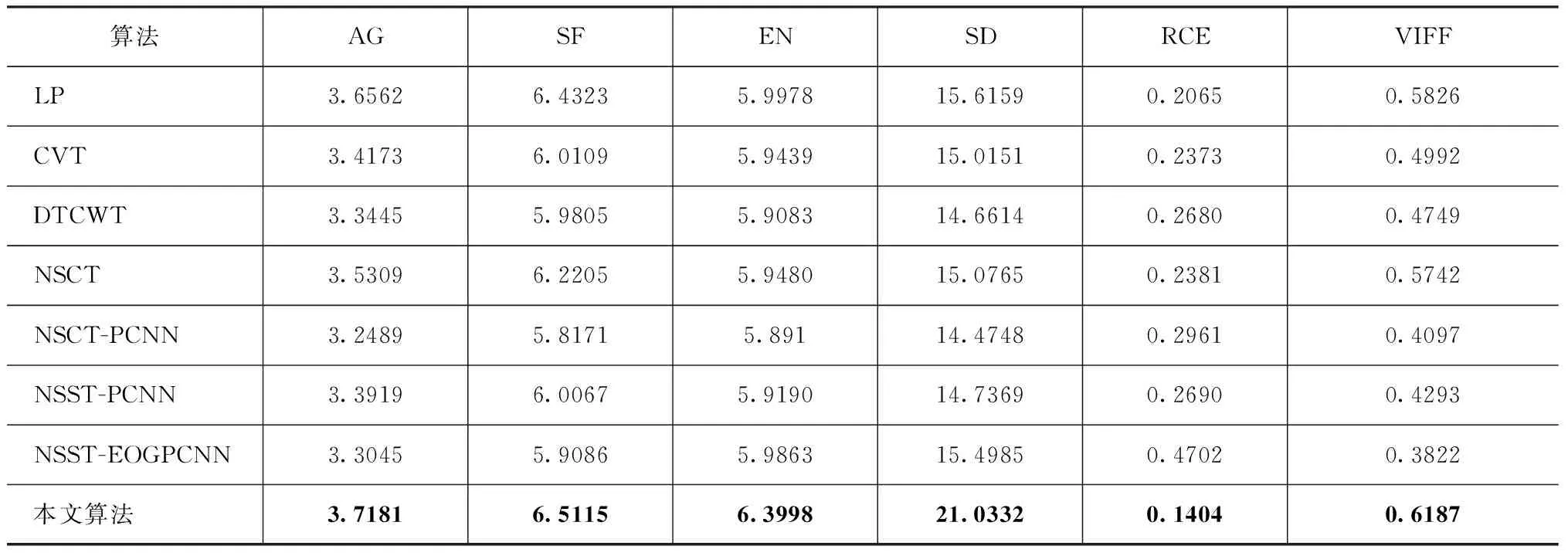
表2 Dune图像融合的客观指标结果Tab.2 Objective index results of Dune image fusion

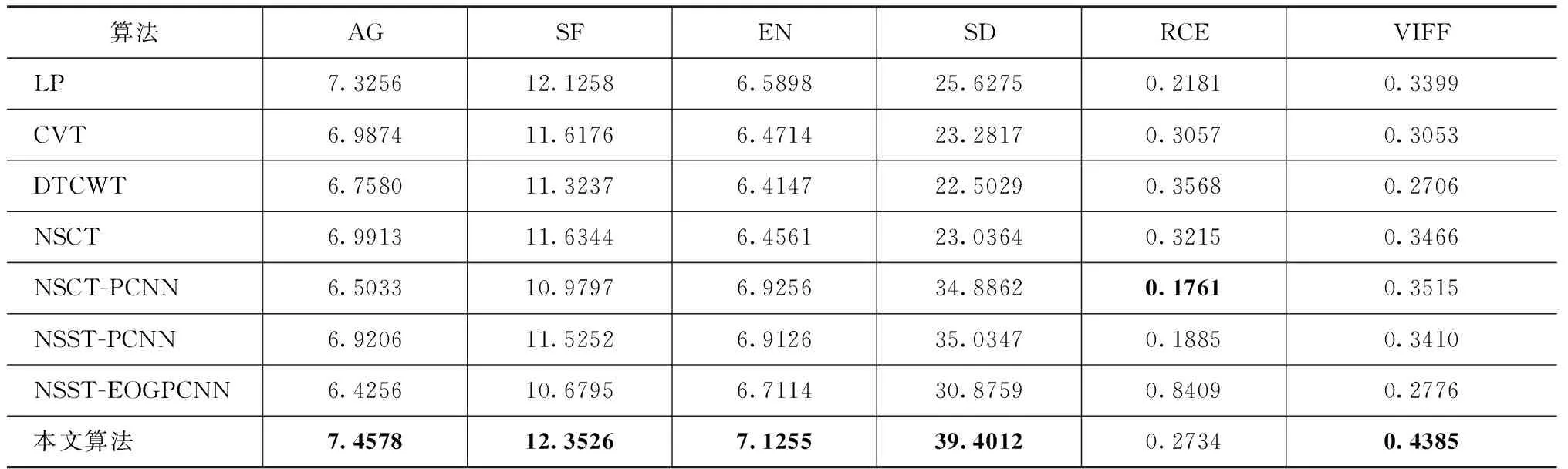
表3 Sandpath图像融合的客观指标结果Tab.3 Objective index results of Sandpath image fusion

5 结 论

本文提出一种基于优化PCNN与区域特征引导法则的红外与可见光图像融合算法,充分利用了NSST的多分辨率特性及各向异性,将图像分解为低高频分量,针对低高频成分各自的特点,提出优化PCNN模型和区域特征引导法则分别对图像低高频分量进行融合。采用3组经典红外与可见光图像对本文算法、7种传统及流行算法进行融合性能对比实验为例,实验结果表明本文算法有效综合了红外与可见光图像各自的优势信息,解决红外与可见光图像融合所存在的边缘信息缺失、目标特征不够突出问题,并在主观视觉和客观指标上均具有明显的优势。