基于平方运算与多重希尔伯特变换的F-P干涉振动测量

华 震,高丙坤,岳航宇,崔翔宇

(东北石油大学电气信息工程学院,黑龙江 大庆 163318)

1 引 言

快速发展的光学技术的一个重要分支是光纤干涉传感器的应用。已经证明这些传感器比电传感器灵敏几个数量级[1],用于无接触的实时自动监测。光纤中的法布里-珀罗(F-P)干涉是一种快速、灵敏的振动分析的工具,它也可以与光纤信号传输相结合,在恶劣的工程环境中获得稳定的性能[2-3]。

干涉信号最初用条纹计数法来恢复振动信息[4],但其分辨率仅为波长的一半,这极大地限制了测量精度。在F-P干涉测量位移的应用中,2018年陈海滨提出了一种以掺铒光纤放大器为光源的F-P干涉位移测量方法[5],但只能实现于11 mm长度范围内1 μm的分辨率,并且实验结构复杂；魏仁选提出了一种F-P干涉的微位移测量方法,利用F-P干涉的光谱相邻波峰之间的波长差与腔长的关系来测量位移,但其需要宽带光源,并且额外需要光谱仪等器件[6]；2005年,张彩妮提出了一种基于F-P干涉的角位移测量原理[7],利用角位移与干涉信号条纹数变化的函数关系,来测量角位移,但是需要把初始入射角调至40°到50°之间。2014年,李春成,王鸣等人提出基于F-P腔干涉的强度解调微位移方法[8],可实现在λ/4范围内,测量误差小于1 nm,但是需要额外的相位调制,增加实验难度。在其他测量位移方法中,张恩政在2013年提出了一种基于数字频率时钟信号的上升条纹锁定的外差干涉相位测量方法[9],但是需要解决外差干涉仪的非线性误差；2016年,崔俊宁等人提出了一种新的零差正交干涉仪,可以大大抑制非线性误差。然而,这种方法需要高度对称的光学结构来获得两束激光之间的平衡干涉[10]。

2 理论分析

2.1 F-P干涉原理

F-P腔是最方便的干涉配置,因为它只是由两个典型的平行镜面之间的空间形成,如图1所示。

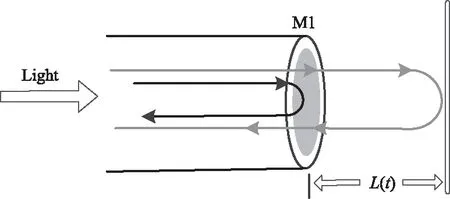
图1 F-P干涉原理图Fig.1 Schematic diagram of F-P interference

自由空间波长为λ的单色光波在两个平行镜面间形成F-P腔,光波在F-P腔内往返出现了相位滞后现象,相位滞后为[11-12]

φ(t)=φ1-φ2=4πnL(t)cosθ/λ

=4πnL(t)/λ

(1)

其中,φ1和φ2是相应两镜面的相位滞后;n是镜面之间介质的折射率;L(t)是镜面间的距离;θ是入射角。如果腔内为空气(n=1)且入射光平行,这时θ=0。在双波干涉仪上叠加信号的平面波近似干涉的帮助下[13-14],FP干涉得到的输出功率P可以表示为:

P=A12+A22+2A1A2cos(φ1-φ2)

(2)

A1和A2是两个镜面反射信号的振幅。

冯一余和保安到卧室门口，就见里边床上和衣躺着一个男的，一身酒气，正打着震天响的呼噜。冯一余吓了一跳，说，喝了酒还敢开车？女主人立刻生气说，你不要乱说啊，他是喝了酒，可车不是他开回来的，是他朋友替他开回来的。保安说，难怪停错了。两个便上前叫那男的，却叫不醒，推也推不醒，拉也拉不起来，醉成一摊泥了。

由公式(1),可推导出L(t)=φ(t)λ/4π

(3)

2.2 平方算法原理

通过直流阻隔和归一化处理,由公式(1)和公式(2),干涉后的输出功率P可以写为:

P=cos(4πL(t)/λ)

(4)

这时P2可以写为:

P2=cos(4πL(t)/λ)·cos(4πL(t)/λ)

=1/2cos(2·4πL(t)/λ)+1/2

(5)

为了不使加倍后的输出功率引入新的常数,公式(5)整体减1/2,得到1/2cos(2·4πL(t)/λ),此公式为条纹加倍的公式,图2为平方算法流程图。

图2 平方算法流程图Fig.2 Flow chart of the square algorithm

对于周期余弦函数,如果目标的最小位移能引起一个条纹变化,设为ΔL。公式(5)中的相位变化量Δφ可以写为:

Δφ=2π=2·4πΔL/λ

(6)

因此,从公式(6)能得到ΔL=λ/4,条纹的精度在此时达到了λ/4,故条纹加倍。

当经过平方运算后,由公式(5)可得,此时的φ(t)=2·4πL(t)/λ,故L(t)=φ(t)λ/8π。

为了验证该算法的有效性,进行了如下仿真。图3给出了目标运动的仿真结果。在图3中,激光波长为1550 nm,运动是驱动频率为100 Hz,零初始相位,振幅为1.55 μm,采样频率为400 kHz,采样点4000个。

图3(a)表示的是原始干涉条纹的图像,由于振幅为1.55 μm,故峰峰值为3.1 μm,由半波长代表一个条纹,故初始条纹4条。图3(b)展示了经过平方算法后的图像,初始参数与图3(a)参数保持一致,由图像可看出条纹增加到8条。故验证了其原理的有效性。

图3 平方运算仿真图Fig.3 Simulation of square arithmetic

2.3 多重希尔伯特变换原理

希尔伯特变换的表达式为:

(7)

希尔伯特变换对原始干涉信号实现π/2的相移,当进行3次希尔伯特变换实现3π/2的相移,则在数学上等价于实现-π/2相移,故可以总结为希尔伯特变换类似于π/2的移相器,即输入一个正弦信号可得出余弦信号,因此可以通过希尔伯特变换得到tan[φ(t)],然后通过相位展开得到φ(t)[15]。

图4(a)展示了F-P干涉信号经多重希尔伯特变换的信号与初始信号,①的信号是初始的干涉信号,②的是干涉信号经多重希尔伯特变换后的信号。图4(b)展示了包裹相位arctan(φ(t))。

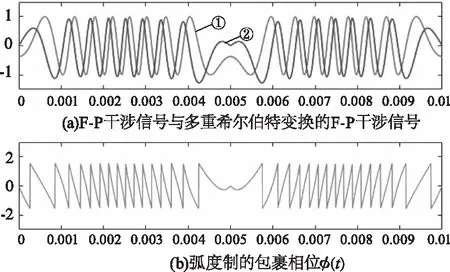
图4 仿真多重希尔伯特变换信号Fig.4 Simulates signals of multiple Hilbert transforms

2.4 数值仿真

为了验证算法的有效性和准确性进行如下的仿真。图5和图6分别展示了基于多重希尔伯特变换的振动重构和基于平方运算和多重希尔伯特变换的振动重构,在图5和图6中,设置激光波长λ=1550 nm,物体运动的驱动频率为80 Hz,零初始相位,并且振幅为A=3.1 μm(A=2λ),采样频率为50000 Hz,采样点为5000,图5(a)表示的初始F-P干涉信号,图5(b)为F-P干涉信号经多重希尔伯特变换后的信号,图5(c)①为原始物体振动位移,②是经该算法重构出的振动位移,图5(d)显示的为重构出的位移与初始位移间的误差。图6(a)表示初始F-P干涉信号,图6(b)表示经平方运算后的干涉信号,图6(c)表示初始信号先经平方运算再通过多重希尔伯特变换后的信号,图6(d)和(e)表示的与图5(c)和(d)表示的一致。对比图5和图6可知,基于平方运算与多重希尔伯特变换的振动重构的精确度明显高于基于多重希尔伯特变换的振动重构的精度。

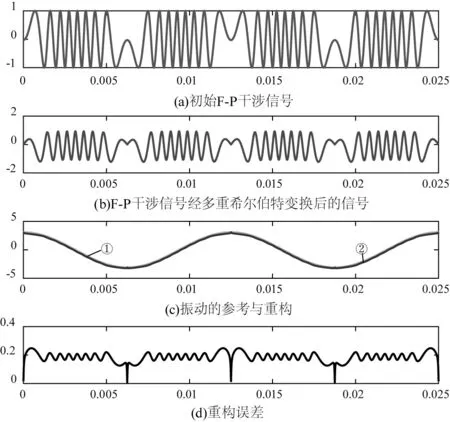
图5 基于多重希尔伯特变换的振动重构仿真图Fig.5 Vibration reconstruction simulation basedon multiple Hilbert transforms

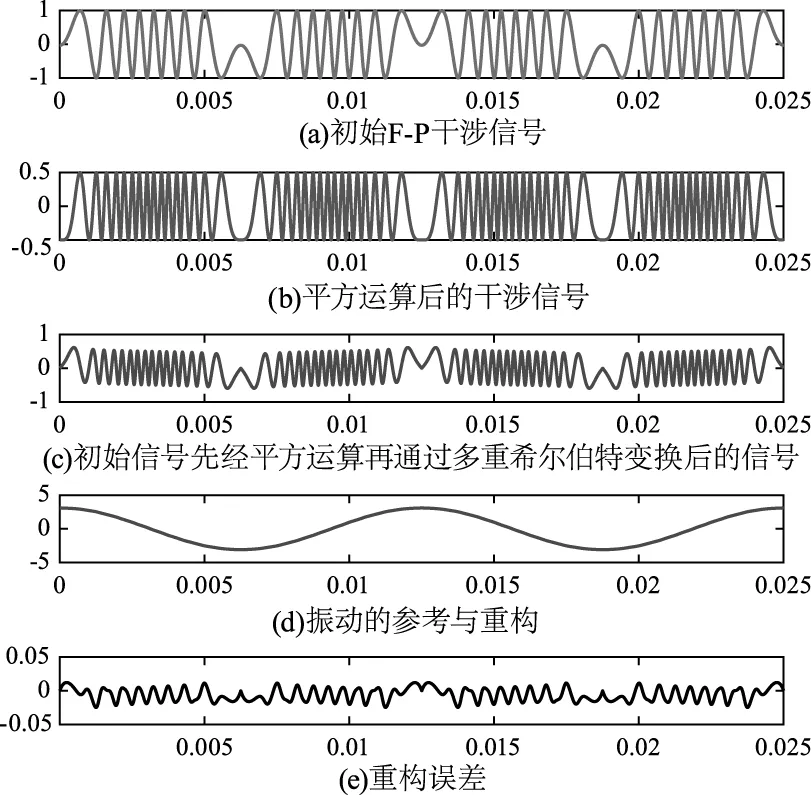
图6 基于平方运算与多重希尔伯特变换的振动重构仿真图Fig.6 Vibration reconstruction simulation diagram basedon square operation and multiple Hilbert transform

3 测量实验与结果

为了进一步证明所提方法的有效性,进行如下实验,图7为实验装置。DFB激光器的波长为1550 nm,DFB激光器与耦合器相连,耦合器其中一个端口的光照射在一面镜子上,其镜子放在压电陶瓷器(PZT)上做振动,另一个端口用于照射在外置PD,用于采集干涉信号,通过数据采集模块(USB-4431,NI)获取电压信号,并在PC上进行处理。

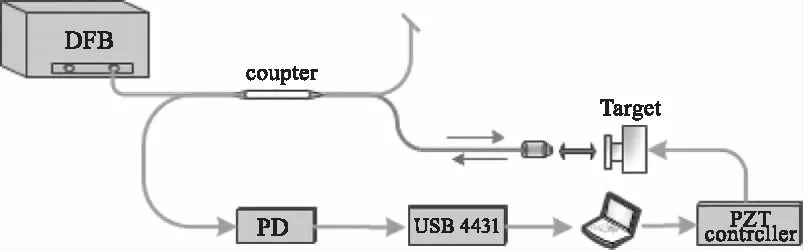
图7 实验装置图Fig.7 Experimental setup diagram

首先,PZT控制的运动频率5 Hz,振动峰峰值为6.2 μm,采样频率为50 kHz,图8(a)展示了实验干涉信号,图8(b)展示了其干涉信号的多重希尔伯特变换后的信号,图8(c)①表示参考振动信号,②为重构的信号,图8(d)显示了重构误差。

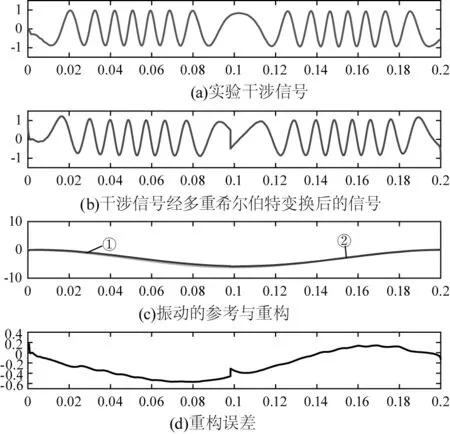
图8 基于多重希尔伯特变换的振动重构实验图Fig.8 Vibration reconstruction experimentaldiagram based on multiple Hilbert transforms

接下来进行基于平方运算与多重希尔伯特变换的振动测量,与图8实验的数据相同,图9(a)显示了实验的干涉信号,图9(b)展示了其经过平方算法后的信号,图9(c)显示了平方运算后的多重希尔伯特变换信号,图9(d)显示了①的参考振动信号以及②的振动重构信号,图9(e)显示了重构误差。由图9(d)所示,重构振动信号的最大误差为5.65 %,由图9(e)所示,重构的最大误差为4.1 %。表1列出其他组实验数据的误差比较。

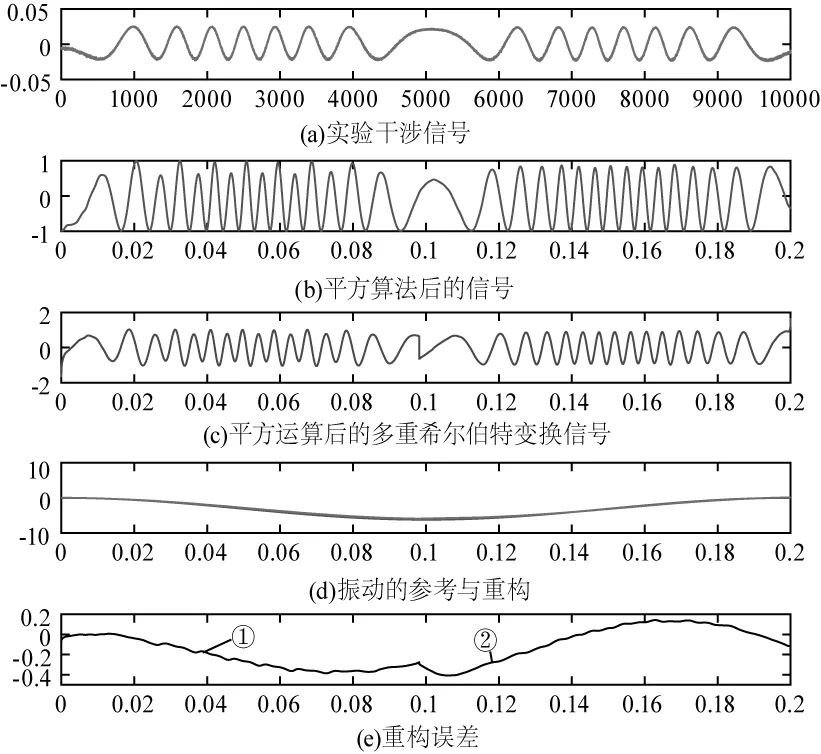
图9 基于平方运算与多重希尔伯特变换的振动重构实验图Fig.9 Vibration reconstruction experimental diagram basedon square arithmetic and multiple Hilbert transforms

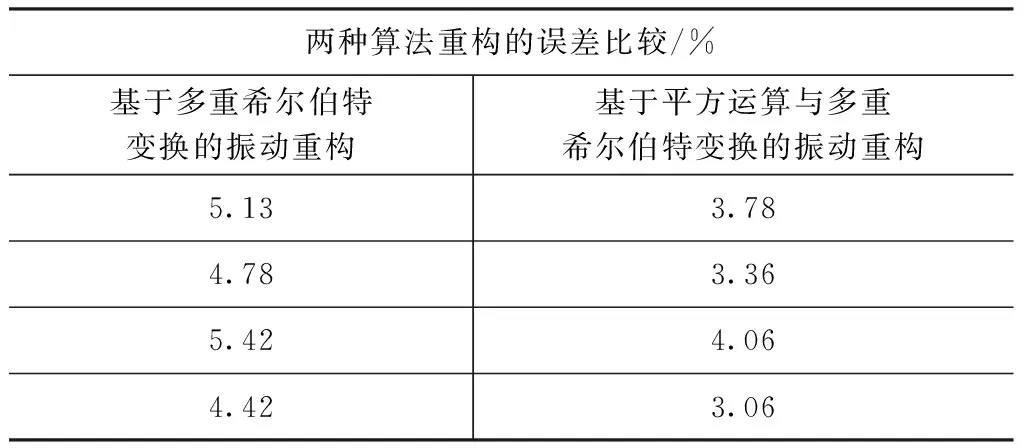
表1 两种算法重构振动的误差比较Tab.1 Comparison of the errors of the twoalgorithms in vibration reconstruction

4 结 论

本文提出了一种快速有效的微振动重构方法。先通过平方算法使F-P干涉条纹加倍,然后对反向点两侧的干涉条纹分别进行一次和三次希尔伯特变换,重组出一组与加倍后信号相差π/2相位的信号,然后重构出物体的振动。并且实验装置结构简单,不涉及任何复杂的计算。实验结果表明:振动测量精度在纳米级,相比于基于多重希尔伯特变换的振动测量可降低误差。