基于EMD分解与1-D CNN算法的光纤振动信号的识别

吴 虎,孔 勇,王振伟,丁 伟,李 欢

(上海工程技术大学电子电气工程学院,上海 201620)

1 引 言

DAS因其抗电磁、监测范围大等优点在管道监测、周界预警、地震预测、入侵检测等领域得到了广泛应用。基于φ-OTDR的DAS与其他光纤入侵传感器相比,具有灵敏度高、全分布方式、成本相对较低、可实现远程入侵检测等优点,是一项很有发展前途的技术[1-5]。在对入侵事件进行识别的过程中,主要可分为四个模块:对入侵振动信号进行预处理；特征提取；制作数据集；使用识别算法进行分类。由于在实际环境中存在大量的振动源,但是对振动事件的识别主要是其中的部分振动,其余的振动信号为噪声,如果不对采集的信号进行滤波处理,对最后的识别结果影响会非常大,因此对振动信号进行预处理是非常有必要的,常用的去噪方式有小波包去噪[6]、变分模态分解(VMD)[7]等,在文献[8]中提出使用EMD将φ-OTDR采集的振动信号分解为一系列的固有模态函数(IMF)和残差分量。使用PCC选择出无振动的位置,通过去除多个IMFs来消除高频噪声,该方式将100 Hz和1.2 kHz的振动事件的信噪比分别提高到42.52 dB和39.58 dB。常用的特征提取方式有提取振动信号的傅里叶变换特征、短时能量、梅尔倒频系数等[9-11],或者使用EMD[12]、VMD[13]、小波变换[14]算法将信号分解后提取相关的统计学特征。典型的分类算法主要有:支持向量机(SVM)[15]、极值梯度下降(XGBOOST)[16]、随机森林树[17]。这些方法虽然可以比较准确地识别出入侵事件的类别,但是其运算量大,非常耗时,所以当DAS的监测距离很大时,这些方式的识别时间会随着监测距离的增加而增加。由于特征提取会耗费大量时间,故开始使用二维卷积神经网络[18]、概率神经网络[19]、多层卷积神经网络[20]结合的方式对振动信号进行识别,在文献[21]中提出使用一维卷积神经网络结合SVM对油气管道入侵事件进行识别,该方式直接将经过预处理的振动信号喂入一维卷积神经网络,达到了与二维卷积神经网络相近的准确率,降低了识别时间。

因此在本次研究提出使用EMD算法分解振动信号,然后再使用PCC选择出有效的IMF分量,并使用WTD对有效的IMF分量进行去噪,将去噪后的IMF分量进行重构,最后将重构信号输入一维卷积神经网络进行识别。实验表明该方式能有效识别出入侵事件类别。

2 识别方式原理

2.1 基于φ-OTDR分布式光纤声传感原理

φ-OTDR[22]的结构与OTDR的结构相近,不同的是φ-OTDR使用的激光器为窄线宽激光器,其注入光为强相干光[23]。φ-OTDR的原理为:在传感光纤中找出三个间隔相等的点,分别命名为a点、b点、c点,a点产生的后向瑞利散射光(BRS)不会与b、c点产生的BRS发生干涉,但是脉冲光由a点传播到c点产生的BRS会与在b点产生的BRS发生干涉,当在c点有振动时,c点的BRS的相位会发生变化,因此干涉后的BRS中携带了由于振动引起的相位变化信息。不同类型的振动事件所引起的相位变化也不同,最后形成的波形也不尽相同,因此可以采用相应识别算法对振动事件波形进行识别。

基于φ-OTDR的DAS结构如图1所示,在图1中,分布式反馈激光器(DFB-LD)作为系统光源,激光经过声光调制器(AOM)后被调制为脉冲光。脉冲光经过掺铒光纤放大器(EDFA)放大后使用带通滤波器(BPF)滤除由EDFA产生的放大自发辐射(ASE)噪声。经过滤波的脉冲光通过光环形器(OC)进入传感光纤,在传感光纤中产生的BRS往回传播。BRS通过OC被注入EDFA中进行放大,并且使用BPF滤除ASE噪声。经过滤波的BRS被光电探测器(PD)转为电信号,最后被DAQ采集。

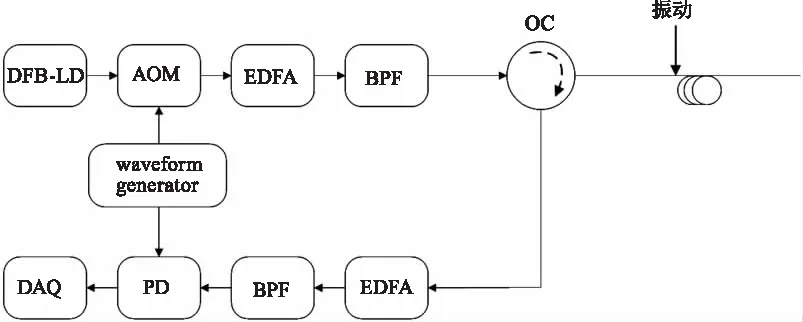
图1 φ-OTDR系统结构图Fig.1 Structure of φ-OTDR system

2.2 EMD分解算法

EMD能将非平稳时间序列、非线性信号分解成K个从高频到低频的IMF分量(Ei)和残余函数(Wi),如公式(1)所示。

(1)

分解出的各分量应满足两点要求:分量信号的极值和过零点数量最多不超过一个；分量信号的任意局部最大包络与最小包络的均值应为0。EMD算法的步骤如下:

(1)得出待分解信号全部的极大值点以及极小值点,使用三次样条插值法得出待分解信号的上包络线与下包络线。

(2)计算出上下包络线均值p(t),将p(t)与待分解信号x(t)相减得到y(t),若y(t)满足IMF条件,则y(t)为首个IMF记为E1,若不满足IMF条件则重复步骤(1)和(2)直到满足IMF条件为止。引入标准差SD判断振源信号分解是否结束,SD值通常在0.2至0.3之间[24]。

(2)

(3)将E1从待分解信号中分离得到W1=x(t)-E1,W1为残差函数。

(4)将步骤(3)得到的W1视为新的待分解信号,重复步骤(1)到步骤(3)得到E2,E3,…,En,当Wn的绝对值很小或者变为减函数时,停止分解。

2.3 PCC

PCC是用来计算两种变量相关性的一种方式。计算PCC会得到两个指标:相关系数(R)、相关指数(P)。其中R的值在-1到1之间,当R越接近于1说明两种变量正相关程度越高,当R越接近于-1说明两种变量负相关程度越高,当R越接近0说明两种变量越不相关。P的值越小说明相关程度越高,P是相关程度判断的第一准则,当P值大于0.05时,不用考虑R值,直接判断两种变量不相关。

PCC的计算公式如下:

(3)

(4)

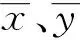
EMD能基于信号本身特性进行自适应分解,但会引入了模态混叠问题[25]。模态混叠出现在IMF分量中会导致该IMF分量不具备物理意义,因此采用PCC计算每个IMF分量与原始信号的R,P。设置一个阈值,当计算得出的P值大于0.05将IMF分量视为无效分量,当P值小于0.05且R值小于0.1,也将该IMF分量视为无效IMF分量将其丢弃。

2.4 一维卷积神经网络

基于LeNet-5 1-D CNN的结构如图2所示,主要包括三个卷积层、三个池化层、两个全连接层、一个softmax分类层。卷积层和池化层主要用于提取一维信号的特征,全连接层主要将提取到的特征映射由多维特征转为一维特征。Softmax分类层输出各类识别事件的概率值,越接近于1说明是该事件的概率越大。在1-D CNN中,通常使用的激活函数为ReLU激活函数,损失函数为交叉熵。

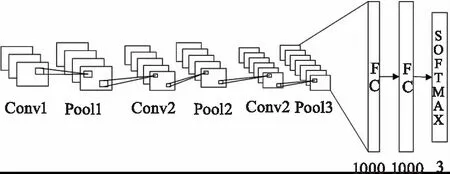
图2 LeNet-5型一维卷积神经网络Fig.2 LeNet-5 one-dimensional convolutional neural network

3 实验验证与结果分析

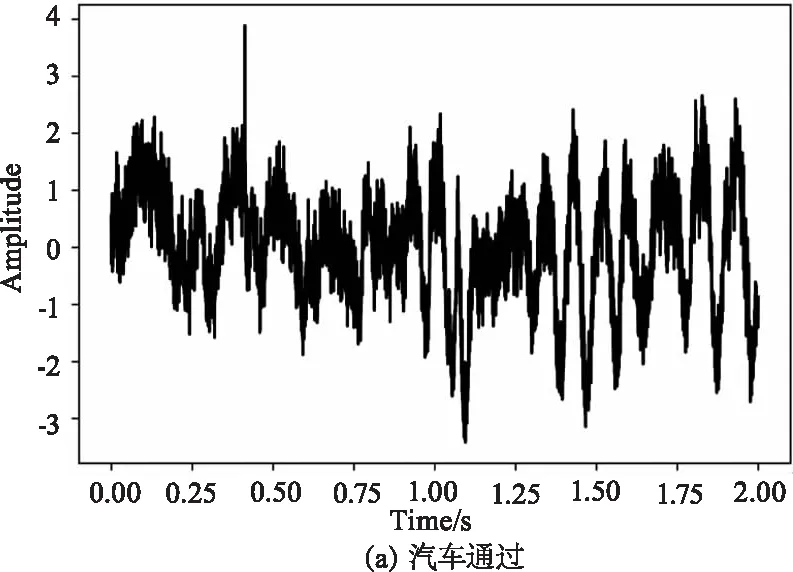
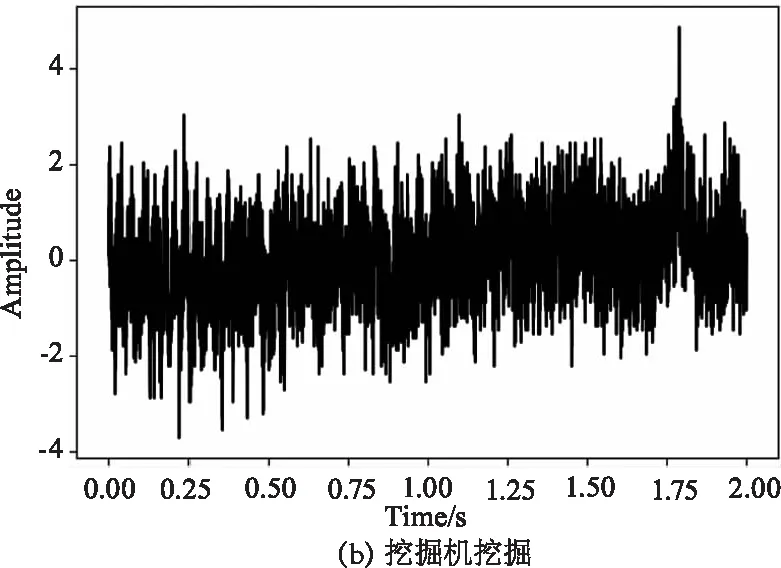
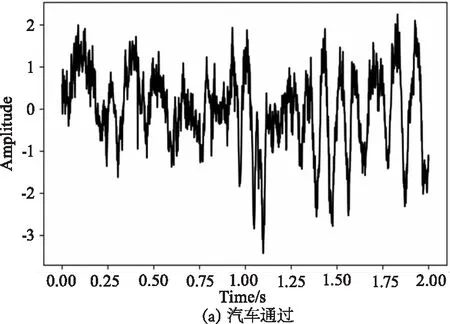
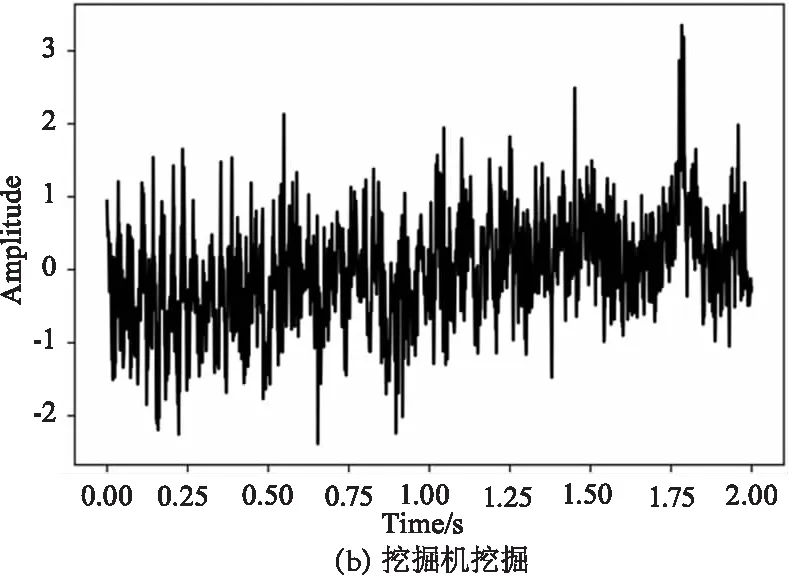
实验系统如图1所示。传感系统采用的是基于φ-OTDR的DAS。该系统使用线宽为3 kHz、输出功率为10 mW的分布式反馈激光器(DFB-LD)作为光源,使用带宽为100 MHz的AOM对激光进行调制,被调制后的脉冲光经过放大增益为27 dB的EDFA进行放大。使用带宽为200 MHz的PD去检测BRS,最后使用采样位数为12位、采样速率为200 MHz/s的DAQ进行信号的采集。传感光纤被埋在中国上海市的文翔东路和沪松路的施工现场中,埋藏深度大约在1～2 m。该分布式传感系统主要采集汽车通过、挖掘机挖掘、破路机工作时的振动信号。其中破路机工作是指将挖掘机铲斗更换为破碎锤进行破碎工作时采集的振动信号。本次研究主要为识别单个振动事件,对于混合型振动事件的识别在目前仍是非常具有挑战性的。采集到的汽车通过、挖掘机挖掘、破路机工作的原始振动如图3所示。

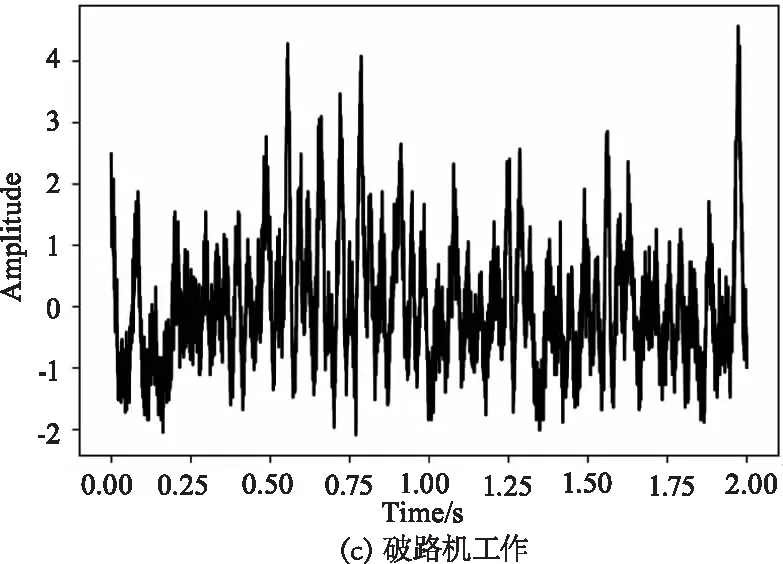
图3 原始振动图像Fig.3 Raw vibration images

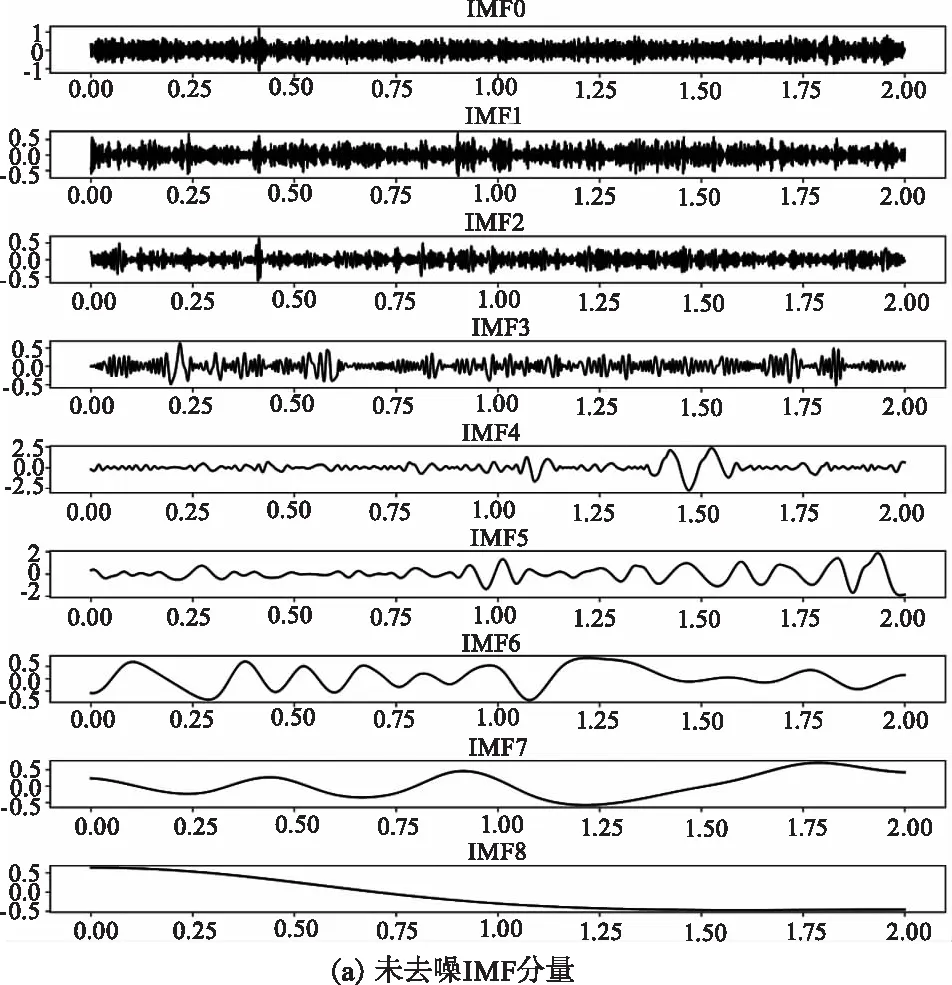
在使用基于φ-OTDR的分布式光纤传感系统采集到各类事件的振动信号后,在每类振动事件中选择出300个样本,每个样本的帧长为2 s,总共900个样本。将每种类型的事件信号进行EMD分解,获得每个振动样本的IMF分量,汽车通过事件的IMF分量如图4所示。图4(a)中,IMF分量未经过WTD,可以看出在IMF分量的高频分量中含有大量噪声,分解出的频率越低含有的噪声越少；图4(b)中,IMF分量经过WTD后,IMF0、IMF1中的大部分噪声被去除,而随着IMF分量的频率越来越低,经过去噪后的变化也越来越不明显。

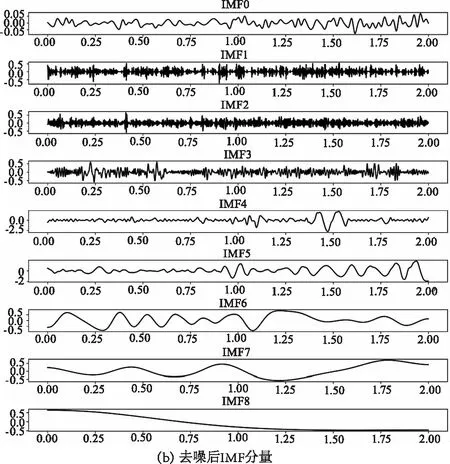
图4 汽车通过振动事件的IMFS分量Fig.4 IMFS component of a vehicle passing a vibration event

得到IMF分量后,计算出每个IMF分量与原事件信号的PCC。如果得出的P值大于0.05则将该IMF分量视为无效分量,反之,再判断其R值是否大于0.1,若小于0.1则也将该IMF分量视为无效信号。得到各个事件振动信号的有效IMF分量后,由于还有部分噪声存在于低频的IMF分量中,故对每个IMF分量进行WTD。将去噪后的各个事件的IMF分量分别求和,得到重构的事件振动信号,汽车通过、挖掘机挖掘、破路机工作的重构信号如图5所示。将得到的900个重构信号样本随机打乱后划分出506个样本作为训练集,225个样本作为验证集、169个样本作为测试集,训练集用于训练识别模型,验证集用于验证识别模型是否有效,测试集用于验证训练好的模型对未知数据是否有效。

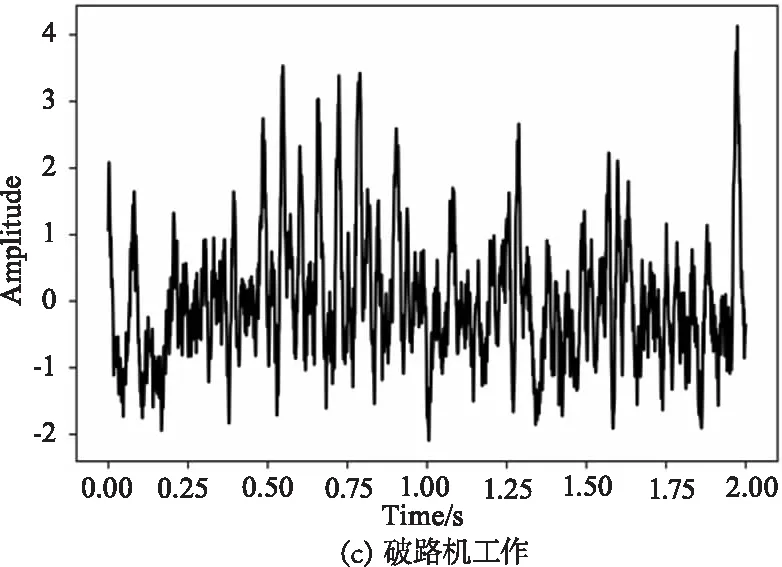
图5 去噪重构信号Fig.5 De-noised reconstruction signal

本次使用的1-D CNN结构如图2所示。该LeNet-5 1-D CNN的参数如表1所示。为了减小1-D CNN的过拟合现象在每个池化层后都加入了Dorpout层,并且全连接层(FC)也使用L2正则化去减小过拟合现象,Dropout层的丢弃率设置为0.2,L2正则化的参数设置为0.01,整个网络的学习率设置为0.01,Optimizer设置为SGD。网络的损失函数使用的是稀疏分类交叉熵(sparse categorical crossentropy)损失函数。1-D CNN网络是使用基于python编程语言的keras框架实现的。

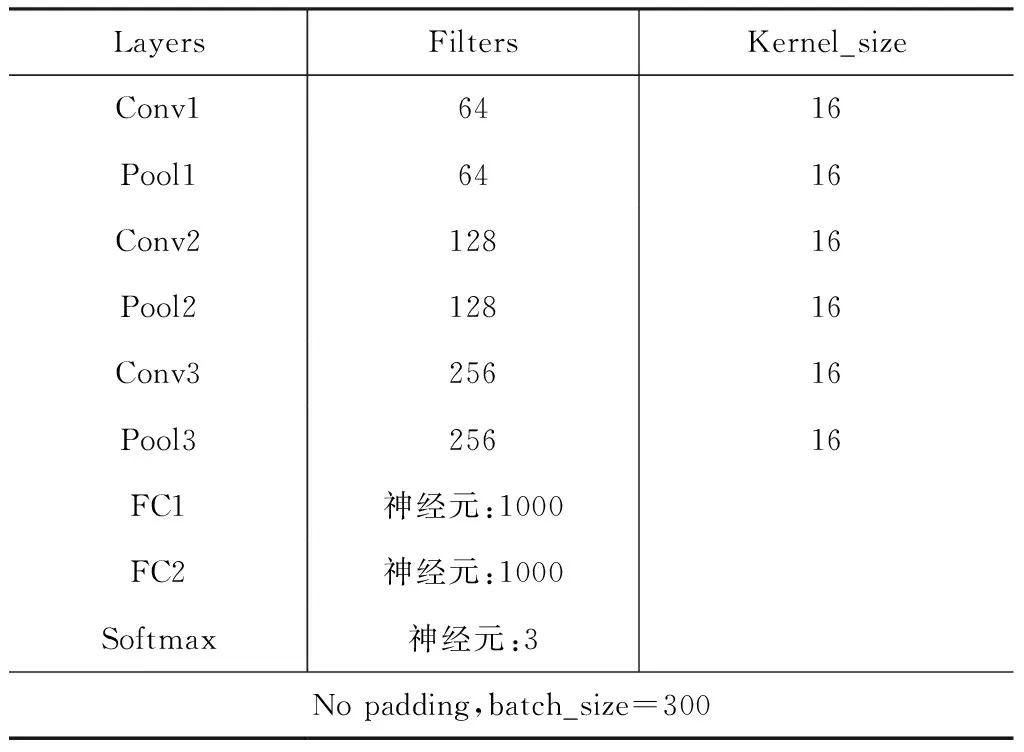
表1 1-D CNN参数Tab.1 Paramenters of 1-D CNN

在本次研究中,对比了使用不同分解算法对最终识别准确率的影响。使用VMD分解算法将振动信号分解为3阶的有限带宽的固有模态分量(BLIMFS)后使用PCC提取出有效的BLIMFS,然后使用WTD对每个BLIMFS进行去噪,最后对所有BLIMFS进行求和得到振动信号的重构信号。使用1-D CNN对重构信号进行识别。两种方式的验证集准确率如图6所示。从图6中可以看出,使用1-D CNN对EMD分解后得到的重构信号的识别准确率明显高于VMD分解后得到的重构信号,这说明使用EMD对振动信号分解后构成的重构信号能更好的表征出不同振动事件的特点。

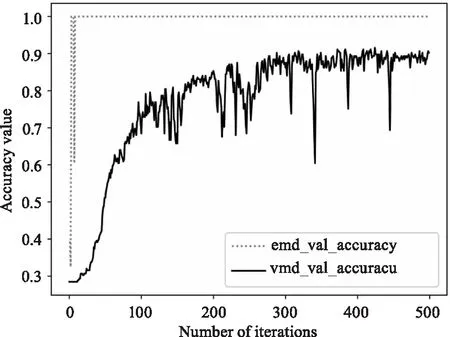
图6 验证集准确率Fig.6 Validation set accuracy

从图6中还可以看出,EMD分解得到的重构信号在进行训练时能更快达到稳定,仅使用不到3 min便能完成训练,因此1-D CNN能在极短时间内完成对新振动事件的训练,这对于快速增加识别事件具有积极意义。将训练好的模型保存,使用测试集对该模型进行测试,测试该模型是否具有很好的泛化能力。1-D CNN对测试集得出的混淆矩阵如图7所示。在图7(a)中,使用EMD分解的方式,1-D CNN对汽车通过、挖掘机挖掘、破路机工作的识别准确率分别为100 %、98 %、97 %；在图7(b)中,使用VMD分解的方式,1-D CNN对汽车通过、挖掘机挖掘、破路机工作的识别准确率分别为95 %、92 %、97 %。使用EMD分解方式的识别准确率更高,这说明使用EMD分解方式重构的信号的可分类性更强,以及训练模型具有很好的泛化能力。

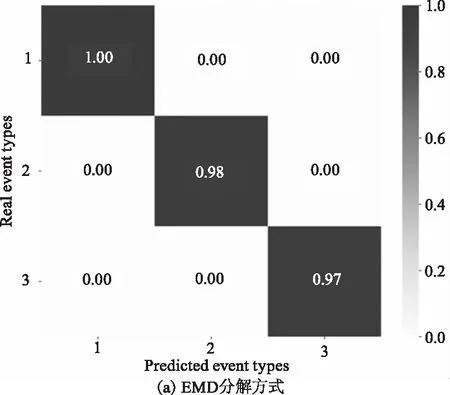
图7 测试集混淆矩阵Fig.7 Test set confusion matrix

4 结 论

提出使用EMD分解算法对光纤入侵振动事件进行分解,使用PCC提取出有效的IMF分量,对有效的IMF分量进行WTD,将去噪后的IMF分量重构为振动信号。重构的事件信号采用1-D CNN进行识别,对汽车通过、挖掘机挖掘、破路机工作的识别准确率分别为100 %、98 %、97 %,平均识别率为98.3 %。