基于RABT火灾曲线的沉管隧道管壁一维温度场解析

2021-09-08吴庆良吴梦军邓小华胡学兵

公路交通科技 2021年8期

吴庆良，吴梦军，邓小华，胡学兵，曹鹏

(1. 招商局重庆交通科研设计院有限公司，重庆 400067；2. 西南大学工程技术学院，重庆 400716；3. 公路隧道建设技术国家工程实验室，重庆 400067；4. 广东省交通集团有限公司，广东广州 510000)

0 引言

沉管隧道由于其地质适应能力强、通行能力强、对周边生态环境影响小且具有不占航道等优势，不仅成为修建跨江越海通道的重要工法，而且在城市水下隧道工程中也得到了广泛应用[1-2]。自19世纪末美国第1次采用沉管法修建水下隧道以来，至今世界上已建成的沉管隧道超过150座[3]。近40 a时间内，我国已建成沉管隧道近20座，包括早期的厦门翔安海底隧道及近期的港珠澳沉管隧道等[4-5]。

在海底沉管隧道给人们生产、生活带来便利的同时，作为主要灾害的火灾也频繁发生，不仅会造成严重的人员伤亡，而且火灾高温还会导致混凝土爆裂和力学性能的劣化，对衬砌结构产生不同程度的损坏，大大降低结构的承载力和安全性。因此，研究隧道火灾发生后隧道衬砌结构厚度方向的温度场分布具有重要意义。

目前已有较多学者针对这一问题开展了大量研究，如蒋树屏等[6]为了解沉管隧道火灾发生时其周围温度场的分布规律及其影响因素，建造沉管隧道试验平台，采用1∶1足尺火灾试验和FDS数值仿真计算相结合的方法，对沉管隧道火灾发生时隧道内温度场的分布规律进行了系统研究。Guo等[7]、张祝永等[8]依托港珠澳大桥沉管隧道工程，利用ANSYS软件分析了火灾下沉管隧道的温度场和应力分布特点。赵志斌[9]以长江隧道为依托，模拟了不同火荷载作用下衬砌结构温度应力的分布规律，并找出了最易破坏的部位。张孟喜等[10]用有限元程序模拟了火荷载作用下沉管隧道结构温度场及应力场，并根据计算结果，结合大量的隧道火灾资料总结了火灾时隧道内部的温度场及应力场的危险区域。Yan等[11]、朱合华等[12]针对特长公路隧道发生火灾特点，借助大比例火灾模型试验，系统研究了火灾时隧道内温度随时间的变化和最高温度与通风风速、火灾规模的关系。

通过文献调研可知，目前有关隧道火灾温度场分布规律方面的研究主要是采用火灾试验和数值模拟2种方法进行，有关隧道在火灾时瞬态温度场演化的解析研究成果相对较少，相对而言，解析解更具备通用性，便于一般规律的探讨，因此，本研究结合沉管隧道遭受火灾时的实际工况建立相应的数学模型，并基于已有初始条件和边界条件，采用2次分离变量法求得RABT火灾曲线的沉管隧道管壁厚度方向的温度场解析解，最后采用广东某沉管隧道参数对管壁不同位置和不同时间的温度场分布规律进行探讨。

1 求解的基本方程

1.1 火灾曲线

为了定量评定隧道衬砌结构的耐火性能，国内外相关单位及学者基于开展的大量足尺火灾试验成果，建立了一系列不同类型的火灾曲线，用来反映隧道火灾时温度随时间的变化历程。国外比较常用的如国际标准化组织制定的 ISO834曲线[13]、美国和加拿大采用的 ASTM-E119曲线[14]，HC曲线和HCint曲线[15]等。

上述各类火灾曲线都体现了隧道内火灾升温速度快这一显著特点，但由于各标准曲线是在不同火灾试验基础上建立起来的，各自的升温过程及达到的最高温度有所差异。我国现行《建筑设计防火规范》(GB50016—2014)[16]在综合考虑上述标准火灾曲线及火灾场景的基础上，对城市隧道承重结构体耐火极限测试时选用的标准升温曲线做出了相应规定，本研究相关内容均是基于该规范中的RABT火灾曲线，函数表达式如下：

(1)

式中，T(t)和T0分别为RABT火灾曲线函数和结构初始温度;t为火灾持续时间。该曲线可以表现汽车在隧道内发生火灾时的燃烧特性，其火灾温度的发展趋势为：火灾时隧道内温度在 5 min 时从常温T0升到最高的 1 200 ℃；最高温度持续了90 min后开始下降；降温过程为30 min，到第125 min时温度将到常温T0。

1.2 数学模型与初始、边界条件

考虑管节的施工制作工艺及空间利用率等方面，目前沉管隧道主要采用矩形截面形状，如港珠澳沉管隧道标准管节的横断面宽度达到37.95 m×11.4 m (宽×高)。在求解沉管隧道沿壁厚方向的温度场分布时，可将研究问题近似简化为如下一维瞬态热传导模型，将衬砌结构混凝土视为均质、连续的介质，且不考虑钢筋、钢纤维的影响。沉管隧道在实际火灾情况下，管节内壁为受火表面，热流温度及沉管结构内表面与热烟气流间的对流换热系数均可测定，属于第3类边界条件。管节外壁处由于被回填土体包围，并且混凝土材料具有热惰性，结构厚度大(一般都超过1.4 m)，其外侧界面温度一般不会太高，与回填土体温差不大，可假定沉管隧道结构混凝土与回填土体之间为理想接触，即不考虑二者之间的接触热阻。

本研究的最终数学模型及初始、边界条件如下。

瞬态热传导微分方程：

(2)

边界条件：

(3)

初始条件：

T(y, 0)=T0(y)，

(4)

式中，T(y,t)为管节结构中任意时刻t任意位置y的温度；相应的T(0,t)为管壁靠海水侧任意时刻的温度；T(d,t)为管壁受火侧任意时刻的温度；T(y,0)为管节任意位置初始时刻的温度；ac为混凝土的导温系数，且ac=λ/cρ，λ，c，ρ分别为混凝土的导热系数、比热容和密度；d为沉管隧道承受火灾处管壁厚度；Tw为隧道外海水和覆土的温度；hf为管节结构内表面与热烟气流间的综合换热系数，即对流换热系数与等效辐射换热系数之和，Tf(t)为管节内壁附近的热流温度，并假定温度分布服从RABT曲线；T0(y)为隧道管壁混凝土的初始温度场分布，火灾常发生在运营隧道，故而可取为常温，即环境的温度Ta。

本研究问题相应的计算模型见图1。为说明一般规律性问题并简化计算，本研究中混凝土的热工参数均取为常数，即不随温度的升高而改变。

图1 计算模型示意图

2 求解的基本方程

工程中由于边界条件的复杂性及方程中物理参数的非线性，造成大多数偏微分方程的解析解求解过程十分困难，并且也仅限于几类特定的数学方法，如分离变量法、拉普拉斯变换、格林函数法等[17]。对于本研究的问题，基于已有初始条件和边界条件，可采用2次分离变量进行求解。

首先对求解问题的边界条件齐次化，令：

T(y,t)=v(y,t)+w(y,t)，

(5)

则求解的数学问题变为下面2个问题。

问题1：v(y,t)是满足基本方程及边界条件的1组特解，通过分离变量法和观察法可构造如下解[18]：

v(y,t)=φ+(η-φ)y/d,

(6)

式中η，φ为待定系数，可代入边界条件求解得：

φ=Tw，

(7)

(8)

式中Tf(t)为RABT曲线方程，函数表达式即式(1)。

问题2：w(y,t)是满足基本方程和齐次边界条件的1组通解，此时初始条件也进行了相应变化，

微分方程：

(9)

边界条件：

(10)

初始条件：

w(y,0)=Ta-v(y,0)，

(11)

式中χ，ω为待定系数，同样根据边界条件求解得：

(12)

(13)

问题2为热传导问题的定解问题，可进一步采用分离变量法和常数变易法进行求解[18]。

下面先采用分离变量法来求解满足边界条件的固有函数系。

令w(y,t)=ξ(y)·ζ(t)，其中ξ(y)，ζ(t)为待定函数，代入方程(10)中有：

ξ(y)·ζ′(t)=ac·ξ″(y)·ζ(t)。

(14)

由于w(y,t)≠0，即ξ(y)≠0,ζ(t)≠0，则上式可变为：

(15)

上式成立，则其必等于同一非正常数(设为-ζ2)，可得：

ξ″(y)+ζ2·ξ(y)=0，

(16)

ζ′(t)+ζ2·ac·ζ(t)=0。

(17)

根据式(16)及相应的边界条件可获得固有函数如下：

ξn(y)=Cn·sin(ζy)，n=1, 2,…,m，

(18)

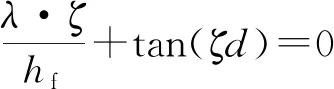
根据常数变易法，假定问题2的特解有如下的形式：

(19)

式中Bn(t)是待定函数；ζn为超越方程λ·ζ+hwtan(ζd)=0的根。为了确定Bn(t)，现按照固有函数系展开成如下级数形式：

(20)

根据正弦函数正交性，可求得：

(21)

式中ψn为系数，可通过下式求解：

(22)

将式(19)和式(21)代入非齐次微分方程(9)，得到：

(23)

由此可得：

(24)

可求得：

(25)

式中Dn为待定系数，代入初值条件进而可求得：

(n=1, 2,…,m)。

(26)

综上可知，本研究问题中海底沉管隧道的一维瞬态温度场的通解为：

sin(ζny)，

(27)

式中，

(28)

(29)

式中，Tf(t)为RABT曲线方程，ζn为超越方程λ·ζ+hwtan(ζd)=0的根。

3 算例验证及分析

以广东某沉管隧道为例，该隧道管节结构采用C50混凝土材料，管壁厚度为1 500 mm。为说明一般规律性问题，本研究取混凝土的热工参数为常数，即导热系数λc=1 W/(m·K)，比热容Cc=1 000 J/(kg·℃)，密度为ρc=2 400 kg/m3，对流换热系数为hc=25 W/(m2·℃)。隧道火灾发生时一般为运营阶段，此时隧道外侧被常温(Tw=20 ℃)的海水和回填土体包围，并假定管节内部已无水化热产生，初始温度场也为常温Ta=20 ℃。

3.1 不同时间的温度分布及解析过程的验证

为验证上述解析解的正确性，采用COMSOL软件建立数值模型，模型尺寸设定为1个混凝土浇注仓大小(3 500 mm×1 500 mm)，模型左右边界设置为热绝缘属性，上边界设置为海水温度Tw=20 ℃，下边界设置为对流热通量，对流换热系数为hc=25 W/(m2·℃)，外部火源温度设置为RABT曲线，其余模型参数与上述算例中一致，完整网格包含10 706 个域单元和286 个边界元，采用瞬态求解器求解，相对容差取0.01。计算模型与125 min结果如图2所示。

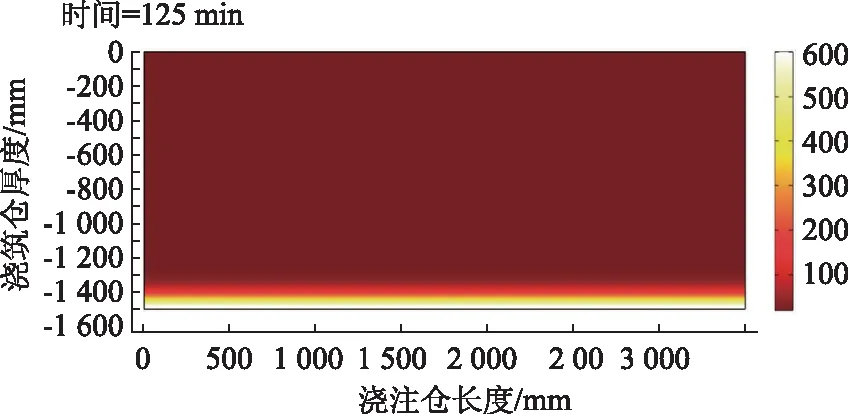
图2 COMSOL计算模型与125 min的计算结果

沿管壁厚度方向取5个监测点(数值模型中y轴正负号对计算结果没有影响，只是坐标系标注不同而已，分别取值y1=1.50 m,y2=1.49 m,y3=1.45 m,y4=1.40 m,y5=1.30 m)。图3为各监测点在125 min的时间域内的温度变化曲线，散点值表示COMSOL模拟计算的结果，曲线值表示解析解的结果。可以看出，不同位置处数值计算结果的散点值均与解析解计算的曲线值重合，说明上述解析解的计算结果与数值模拟结果是吻合的，由此验证了解析解的正确性。

从图3可以看出，管壁靠受火面位置y1=1.50 m,y2=1.49 m这2处的温度在关键时间节点处有突变，如在t=5 min之前，曲线斜率较大，而之后斜率逐渐变小，即温度增长速度变缓；而在t=95 min之后曲线斜率变为负值，曲线开始下降，进入降温阶段，且更靠近管壁受火面位置y1=1.50 m处的降温速度更快。

在沉管管壁上各测点的时间-温度曲线和RABT曲线并不是严格一致，原因主要是由于混凝土材料的比热容造成了温度传递的滞后。受此滞后效应影响，在火灾恒温阶段时(5 min

从图3还可以看出，在火灾升温、恒温和降温全过程中，位置y5=1.30 m处的温度变化都很小，即火灾高温对沉管管壁的影响深度在20 cm左右，这与参考文献[11]中的相关结论也较为吻合。

图3 管壁不同深度处温度场随时间的分布规律

3.2 沿管壁厚度方向的温度分布规律

图4给出了管壁30 cm范围内的Ti=5，10，30，60，95，125 min,i=1,…,6共6个具有代表性的时间点的深度-温度曲线。可以看出，除T6=125 min 时间点外，其他5条曲线呈现明显的单调递减规律，即温度从外到内依次降低；而在T6=125 min 时刻，管壁内部某些区域的温度高于外侧，即有较高的残余温度，主要原因仍是由于混凝土材料热惰性造成温度传递滞后的影响。

图4 不同时间点的管壁温度场随深度的分布规律

管壁温度内高外低现象主要发生在降温阶段(95 min

图5 降温阶段不同时间点的管壁温度场随深度的分布规律

从图5可以看出，降温过程中，在T5=119 min，T6=125 min这2个时刻，管壁内部某些区域温度高于外部，分析原因主要有2方面：一方面是由于3.1节所提到的混凝土材料的热惰性影响，内部温度持续增长，另一方面因为管节腔体内火源温度被降下来之后(119 min时为256 ℃，125 min时为常温20 ℃)，而管壁对应时间的温度分别为663.21 ℃和563.23 ℃，会反向散热，对隧道腔体产生热辐射和热对流，温度下降较快。